Два металлических стержня расположены
Обновлено: 06.05.2024
Учебной программой дисциплины предусматривается выполнение студентами самостоятельной работы с индивидуальными заданиями. Содержание и количество задач для самостоятельной работы устанавливается преподавателем в соответствии с рабочей программой дисциплины.
Выбор варианта задания производится самим студентом по начальным буквам своей фамилии, имени и отчества по таблицам, которые приводятся к каждой задаче.
Эти таблицы составлены следующим образом. Первый столбец содержит буквы алфавита. Во втором столбце указаны номера схем по соответствующему рисунку. В остальных столбцах приводятся исходные данные, необходимые для решения задачи.
Против начальной буквы своей фамилии по горизонтали из второго столбца определяется номер схемы. Числовые данные к принятой схеме выбираются также по горизонтали следующим образом: против начальной буквы своего имени из нечетных столбцов, а против начальной буквы своего отчества из четных столбцов.
3.1. Растяжение и сжатие
Задача 1. Стальной стержень (модуль ЮнгакН/см 2 ) находится под действием внешних осевых сили(рис. 3.1). Построить эпюры продольных сили нормальных напряжений. Оценить прочность стержня, если предельное напряжение (предел текучести)кН/см 2 , а допускаемый коэффициент запаса. Найти удлинение стержня. Исходные данные взять из табл. 3.1.
Исходные данные к задаче 1
Номер схемы (рис. 3.1)
Продолжение табл. 3.1

Пример 1. Стальной стержень (модуль ЮнгакН/см 2 ) с размерамисм;см,см и площадью поперечного сечения нижнего участкасм 2 , а верхнего –см 2 нагружен внешними осевыми силамикН икН (рис. 3.2). Построить эпюры продольных сили нормальных напряжений. Оценить прочность стержня, если предельное напряжение (предел текучести)кН/см 2 , а допускаемый коэффициент запаса. Найти удлинение стержня.

Рис. 3.2

Определяем значение опорной реакции , возникающей в заделке.
Учитывая, что , направим опорную реакциювниз. Тогда из уравнения равновесиянаходим:

кН.

Строим эпюру продольных сил .
Разбиваем длину стержня на три участка (рис. 3.2, а). Границами участков являются те сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений (РОЗУ). Делаем по одному сечению в произвольномместе каждого из трех участков стержня.
Начнем с сечения 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2,б). Само сечение1 – 1 мысленно считаемнеподвижным. Мы видим, чтовнешняясиларастягиваетрассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этомурастяжению. Это противодействие мы заменимвнутреннейпродольной силой, направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении1 – 1внутренняя продольная силауравновеситвнешнюю силу. Поэтому очевидно, что

Переходим к сечению 2 – 2(рис. 3.2,в). Внешняя силарастягивает рассматриваемую нами нижнюю часть стержня, а силаее сжимает (напомним, что2 – 2 мы мысленно считаемнеподвижным). Причем, согласно условию задачи,. Чтобы уравновесить эти две силы в сечении2 – 2должна возникнуть внутренняя сила, противодействующаясжатию, то есть, направленная к сечению. Она равна:

Делаем сечение 3 – 3(рис. 3.2,г). Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная силадолжна уравновесить внешнюю (реактивную)сжимающую силу. Поэтому она направлена к сечению и равна:


Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействуетсжатию. Она равна


При построении эпюры продольных сил будем пользоваться следующим правилом знаков:внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию.
Это правило знаков вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любомсечении нижнего участка стержня внутренняя продольная сила противодействуетрастяжениюи равнакН. В любом сечении среднего и верхнего участков стержня имеет место деформациясжатия, поэтомукН.

Для построения эпюры продольных сил проводимтонкойлинией ось, параллельную оси стержняz (рис. 3.2,д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем»горизонтальнымилиниями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирнойлинией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем, изменение поперечного размера стержня, как это видно из рис. 3.2,д, никак не сказывается на характере эпюры.

3. Строим эпюру нормальных напряжений .
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле

,
где и– соответственно, продольная сила и площадьk–го поперечного сечения стержня.
В первом поперечном сечении стержня нормальное напряжение равно

кН/см 2 ,


кН/см 2 .
Строим по вычисленным значениям эпюру (рис. 3.2,е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюрыN, на эпюре«скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня.
Сопоставляем наибольшее(по модулю) нормальное напряжение, которое в нашем примере возникает во втором сечении стержня, сдопускаемымнапряжением . Напомним, что допускаемое напряжение представляет собой долю отпредельногонапряжения, то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, какпластичного материала,начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести:. Тогда


Условие прочности имеет вид . В нашем случае
кН/см 2 > кН/см 2 ,
следовательно, прочность стержня на втором участке не обеспечена.

Таким образом, площадь поперечного сечения стержня на втором участке, равную см 2 , нам необходимоувеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемуюплощадь поперечного сечения стержня на втором участке:
см 2 .

Принимаем на втором участке см 2 .

5. Вычисляем удлинение всего стержня .
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле


где E – модуль Юнга, а– длина соответствующего участка стержня.

см.

Таким образом, длина стержня уменьшается на мм.
3. Пример решения и оформления задачи
Задача. Два металлических стержня расположены вертикально и замкнуты вверху проводником. По этим стержням без трения и нарушения контакта скользит металлическая перемычка длиной 30 см и массой 5 г. Вся система находится в однородном магнитном поле с индукцией 2 Тл. Направление линий индукции перпендикулярно плоскости рамки. Установившаяся скорость движения перемычки равна 0,2 м/с. Найти сопротивление перемычки. Сопротивлением стержней и провода пренебречь.

= 0,2 м/с
При движении перемычка пересекает линии магнитной индукции и в ней возникает ЭДС индукции, значение которой определяется по закону Фарадея-Ленца:
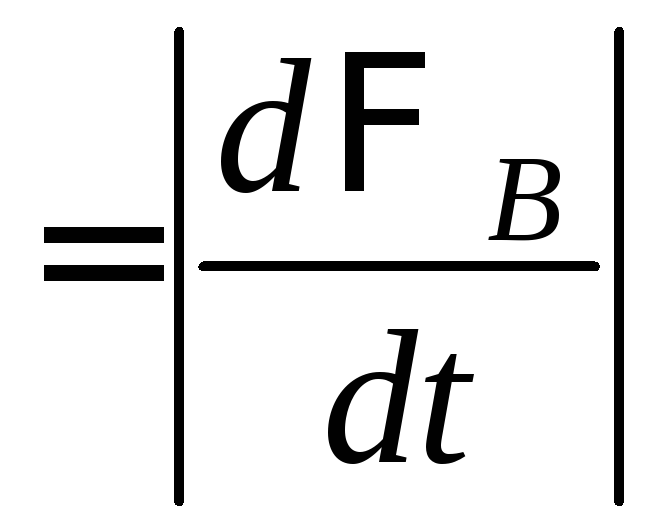
E . (1)
Магнитный поток, проходящий через поверхность, пересекаемую перемычкой за время dt, вычисляется по формуле:

dФВ = BdScos = , (2)
г – угол между нормалью к рамке и вектором индукции магнитного поля, = 0.
Причиной возникновения ЭДС в движущемся проводнике является сила Лоренца, которая дейст-вует со стороны магнитного поля на свободные электроны, движущиеся вместе с перемычкой. Под действием этой силы свободные электроны станут смещаться влево и заряжать левый конец перемычки отрицательно, а правый положительно (рис. 2).
По контуру потечет ток I (см. рис. 1), сила которого рассчитывается по закону Ома:
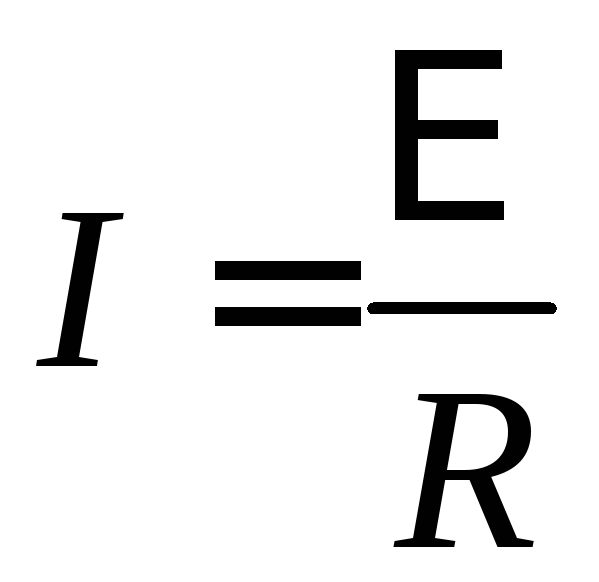
, (3)
где R – сопротивление цепи, которое по условию задачи равно сопротивлению перемычки.
На перемычку с током в магнитном поле действует сила Ампера:
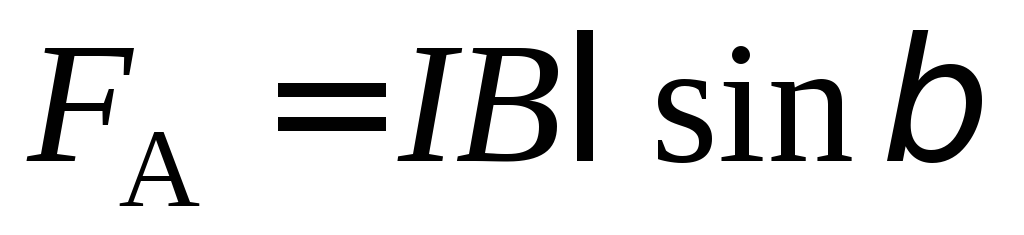
, (4)
где – угол между направлением силы тока и вектором магнитной индукции, = 90.
Подставим формулы (1) (3) в уравнение (4) и получим:
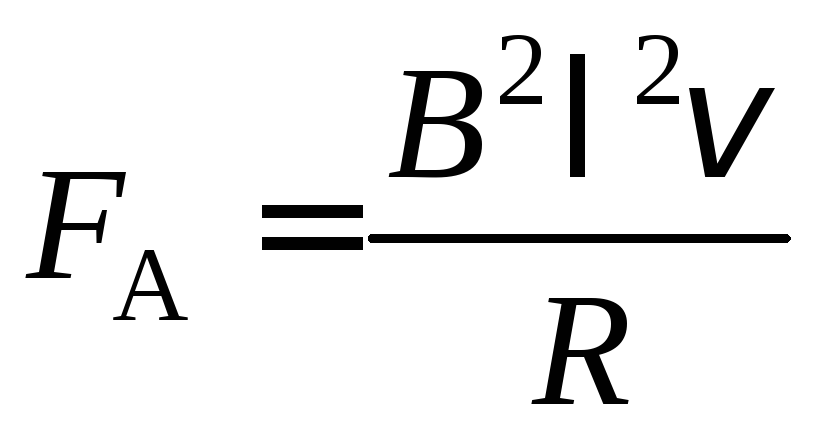
. (5)
При анализе формулы (5) видно, что чем больше скорость движения перемычки, тем больше сила Ампера. При равенстве силы Ампера силе тяжести, действующей на перемычку, ее движение станет равномерным, а скорость – постоянной (см. рис. 1). Запишем условие равенства сил:

mg = . (6)
Подставим выражение для силы Ампера (5) в уравнение (6):
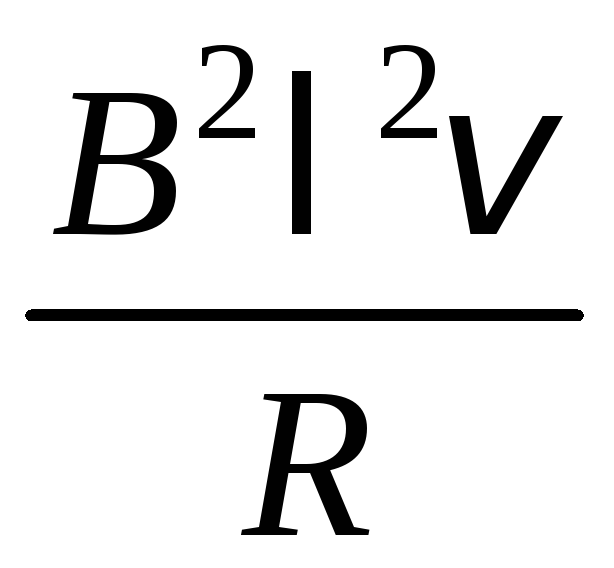
mg = . (7)
Выразим из равенства (7) сопротивление R и получим расчетную формулу:

. (8)
Подставим данные задачи в формулу (8):

(Ом).
Способ 2 (более короткий)
По закону сохранения энергии вся работа силы тяжести (т. е. убыль потенциальной энергии mgh) идет на нагревание проводника. Это связано с тем, что проводник движется с постоянной скоростью и изменения кинетической энергии не происходит, т. е.
mgh = Q, (9)
где h – высота, на которой находится перемычка.
Количество тепла Q можно определить по закону Джоуля-Ленца:
Q = I 2 Rt. (10)
Подставим формулу (3) в уравнение (10):
Q = =, (11)
а уравнение (11) – в формулу (9):
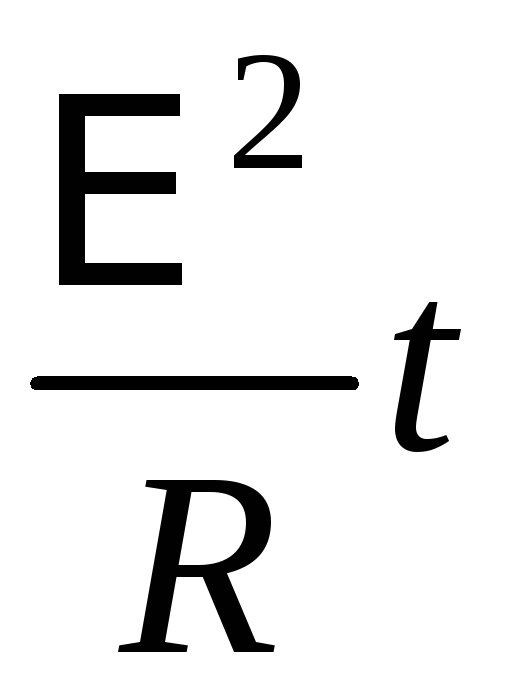
mgh = . (12)
Выразим из тождества (12) сопротивление перемычки:
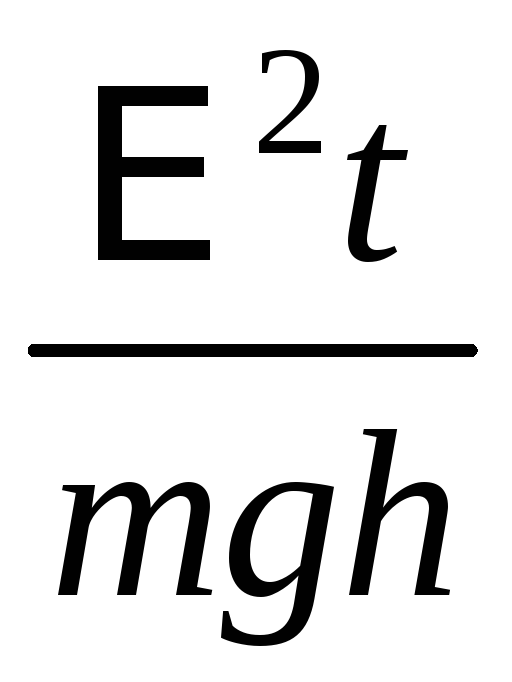
R = . (13)

Расстояние, которое перемычка пройдет за время t с постоянной скоростью

h = t. (14)
ЭДС индукции, возникающая в проводнике, движущемся с постоянной скоростью в магнитном поле, выразим через характеристики проводника и поля:
, (15)
где = 90, sin = 1.
Подставим уравнения (14) и (15) в равенство (13) и получим расчетную формулу:
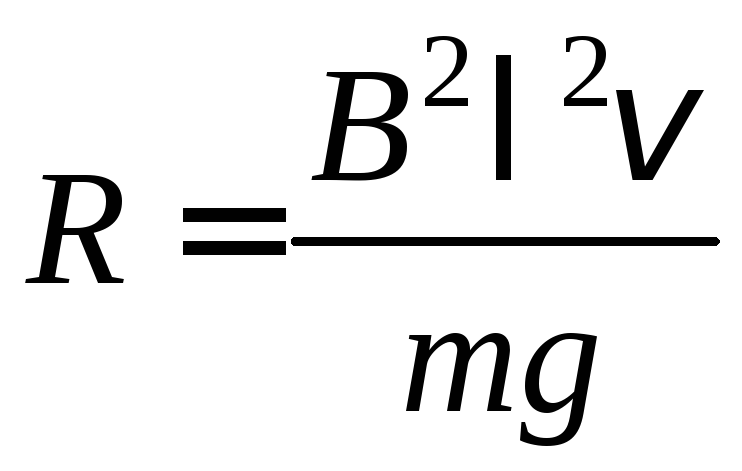
. (16)
Формула (16) полностью совпадает с расчетной формулой (8), полученной при решении задачи способом 1.
Задача с1
Стальной стержень переменного сечения находится под действием двух продольных сил , приложенных по оси стержня (рис.1, табл.1).
Построить эпюры поперечных сил, напряжений и перемещений. Весом самого стержня пренебречь.
При расчете можно принимать: площадь сечения А=10 см 2 , длина участков а=с=1м, b=2м, модуль упругости при растяжении для стали E = 2*10 5 МПа, силы F1 и F2 направлены вниз, а F3 и F4 – вверх.
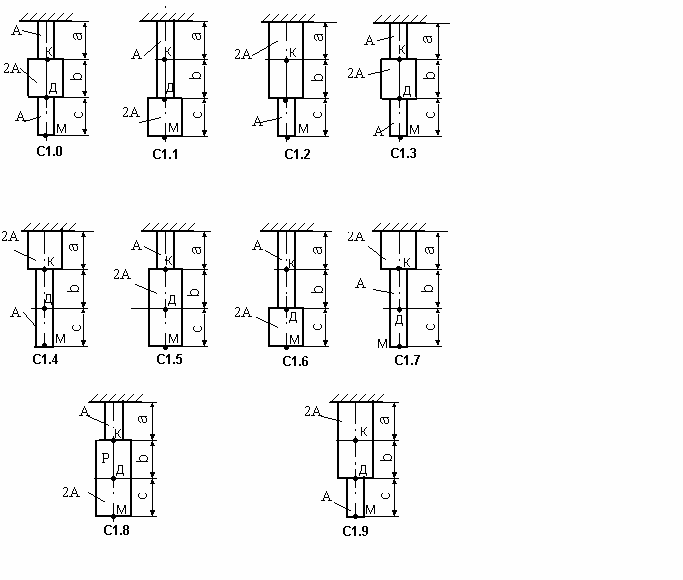
.Пример С1. Стальной стержень находится под действием двух сил F1=200кН и F2=100кН (рис1.1).
Площадь сечения А=10 см 2 , длина участков а=с=1м, b=2м, материал –сталь ( E = 2*10 5 МПа).
Построить эпюры продольных сил, напряжений и перемещений. Весом самого стержня пренебречь.
Решение. 1. Рассматриваем равновесие каждого участка стержня
в виде суммы проекций всех сил на вертикальную ось:Участок МД: N1-F1=0, N1=F1=200 кН.
Участок ДК: N2-F1=0, N2=F1=200 кН.
Участок КН: N3-F1+F2=0, N1=F1 – F2=100 кН.
По этим данным строим эпюру продольных усилий (рис.1.1).
Участок МД: Участок ДК: Участок КН:По этим данным строим эпюру напряжений (рис.1.1).
3.Определяем перемещения каждого характерного участка
где N – усилие на данном участке, L- длина участка, Е – модуль упругости, А- площадь сечения.
Расчеты производим в системе СИ, то есть 1кН=10 3 Н, 1МПа=10 6 Па, 1 см 2 =10 -4 м 2 .
Перемещение сечения К:
Перемещение сечения Д:
Задача с2
Абсолютно жесткий брус опирается на шарнирно-неподвижную опору в точке О и прикреплен к двум стальным стержням с площадями поперечных сечений А и 2А при помощи шарниров (рис.2). На стержень действует сила F1, направленная вниз, или F2, направленная вверх, величины и точки приложения которых приведены в таблице 2. Во всех вариантах принять а=2м, b=1,5м, с=1м.
1) Найти усилия в стержнях
2) Определить диаметры стержней при допускаемом напряжении

Найти усилия в стержнях, определить площади поперечных сечений и диаметры стержней .
Решение. Для определения усилий в стержнях пользуемся методом сечений (рис.2.1,а). Рассекаем первый и второй стержни и прикладываем усилия N1 и N2. Отбрасываем опору 0, а её влияние на систему заменяем реакциями Rox и Rоу.
Рассмотрим систему в равновесии, т.е. составим уравнения статики
, Rох+N2cos . (1)
, Roy+N1-F+N2sin . (2)
N1a-F(a+c)+N2sin (а+b+c)=0. (3)
Заметим, что в эти три уравнения входят четыре неизвестных: Rox; Rоу;N1; N2, т.е. эта система является один раз статически неопределимой, т.к. четыре неизвестных минус три уравнения равновесия равно единице.
Для раскрытия статической неопределимости системы (т.е. для составления недостающего уравнения) рассмотрим картину деформации всей системы (рис.2.1,б). Под действием силы F первый и второй стержни будут сжиматься. Деформацией бруса пренебрегаем. Левый конец бруса находиться в шарнирно неподвижной опоре. Точка В бруса переместиться в точку В1, а точка Е в Е1. Новое положение второго стержня показано пунктиром, а новым положением бруса является прямая АЕ1.
Отрезок ВВ1 представляет собой деформацию первого стержня Чтобы найти деформацию второго стержня, нужно из нового положения этого стержня опустить перпендикуляр Е1К на его старое направление. Этот перпендикуляр отсечет отрезок ЕК, который и является деформацией второго стержняВеличины свяжем из подобия треугольниковОВВ1 и ОЕЕ1 - составим пропорцию:
; ,
отрезок ЕЕ1 выразим из прямоугольного треугольника ЕЕ1К:
Подставляем значение этих отрезков в пропорцию;
Получили четвертое недостающие уравнение, которое называют уравнением совместимости деформаций, но оно пока в сжатом виде. Чтобы его развернуть, нужно деформации стержней расписать по известной формуле:
где - площадь сечения первого стержня, Е – модель упругости материала.
Аналогично для второго стержня:
; .
Подставляем эти выражения в уравнение (4):
После сокращений и преобразований получим:
это и есть развернутое уравнения совместности деформаций. Решая совместно уравнение (3) и (5) найдем усилия в стержнях.
Из уравнения (5) :Значение N2 подставим в уравнение (3)
откуда .
Площади поперечного сечения стержней находим из условия прочности при растяжении стати :
;
.
Так как по условию задачи А1=А, А2=2А, принимаем окончательное значение площадей сечений: А1=10,9 см 2 ,Читайте также:
