Два одинаковых металлических шарика радиуса r

Обновлено: 20.09.2024

Электрический ток может протекать не только «концентрировано», по проводам. Движение электрических зарядов может занимать определенную область проводника, при этом векторное поле плотности тока $~\vec j(x,y,z)$ , не обязательно является однородным, а представлять достаточно сложную структуру. Расчет электрического сопротивления между различными точками среды в этом случае принципиально отличается от рассмотренных выше. Особо отметим, что электрическое сопротивление среды зависит не только от ее свойств (удельного электрического сопротивления), но и от распределения токов в среде. Проиллюстрируем это положения двумя примерами, заодно и покажем методы расчета сопротивления для пространственно распределенных токов.

Пример 1. Пространство между двумя концентрическими хорошо проводящими сферами радиусами r₁ и r₂ заполнено слабопроводящим веществом с удельным электрическим сопротивлением ρ (рис. 288). Определим сопротивление среды между сферами.

Оговорки о проводимости сфер и среды между ними позволяют использовать следующие приближения:

- считать потенциалы сфер постоянными и пренебречь их сопротивлением; - пренебречь объемными зарядами в пространстве между сферами, которые, в принципе, могут возникать при протекании электрического тока.

Для расчета сопротивления среды между сферами положим, что на внутренней сфере поддерживается постоянный электрический заряд +q (то есть сфера подключена к источнику тока, который компенсирует заряд, стекающий с него через проводящую среду). Электрическое поле в пространстве между сферами эквивалентно полю точечного заряда +q, помещенного в центр сфер. Следовательно, разность потенциалов между сферами может быть рассчитана по знакомой из электростатики формуле

Так как система обладает сферической симметрией, то вектор плотности электрического тока $~\vec j$ во всех точках направлен радиально (вдоль прямой проходящей через центр сфер).

Задание для самостоятельной работы.

Докажите, что модуль вектора плотности тока убывает обратно пропорционально квадрату расстояния до центра сфер.

Непосредственно у поверхности внутренней сферы напряженность электрического поля равна

По закону Ома плотность тока у поверхности сферы равна

Так как вектор плотности тока направлен радиально, то есть по нормали к поверхности сферы, и постоянен по модулю, то сила электрического тока, стекающего со сферы, равная потоку вектора плотности тока, равна произведению плотности тока на площадь сферы $~I = jS = \frac E = \frac \cdot 4 \pi r^2_1 = \frac$ . Зная силу тока и разность потенциала, электрическое сопротивление рассматриваемой системы определим по закону Ома

Как и следовало ожидать, полученное значение сопротивления не зависит от «придуманного» заряда внутренней сферы.

Итак, суть использованного метода сводится к независимому расчету разности потенциалов и силы тока между сферами, при заданном значении заряда сферы. Величина этого заряда сокращается при вычислении сопротивления.

Интересно отметить, что если расстояние между сферами Δr = r₂ - r₁ значительно меньше их радиусов, то в знаменателе формулы (4) можно пренебречь различием в их радиусах, тогда знаменатель упрощается $~4 \pi r_2 r_1 \approx 4 \pi r^2 = S$ , то есть становится равным площади поверхности сферы. В этом случае полученная формула (4) превращается в банальную $~R = \rho \frac$ .

Если радиус внешней сферы устремить к бесконечности ($~r_2 \to \infty, \frac \to 0$), то рассматриваемая система превращается в заряженный шарик, помещенный в бесконечную проводящую среду. В этом случае сопротивление среды от шарика радиуса r до «бесконечности» оказывается равным

Пример 2. Два одинаковых металлических шарика, радиусы которых равны r, находятся на большом расстоянии a (a >> r) друг от друга в слабопроводящей среде с удельным электрическим сопротивлением ρ (рис. 289). Вычислим электрическое сопротивление среды между шариками.

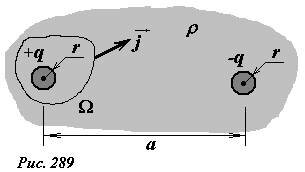
Для расчета электрического сопротивления мысленно сообщим шарикам электрические заряды, равные по величине и противоположные по знаку (+q,-q). Так расстояние между шариками значительно больше размеров шарика, то можно пренебречь влиянием заряда одного шарика потенциал другого, тогда разность потенциалов между шариками определяется по формуле

где φ + , φ - - потенциалы положительно и отрицательно заряженных шариков, соответственно.

Распределение напряженности электрического поля (и соответствующей ему плотности тока) в данном случае достаточно сложной [1] . Однако для вычисления силы тока, стекающего с одного из шариков, знание его не требуется. Мысленно окружим положительно заряженный шарик произвольной замкнутой поверхностью Ω. Поток вектора плотности тока через эту поверхность и будет равен суммарной силе тока между шариками $~I = \Phi_$ . По закону Ома плотность тока пропорциональна напряженности электрического поля $~\vec j = \frac \vec E$ ; так как поток пропорционален этому вектора, то такое же соотношение будет выполняться и для потоков векторов плотности тока и напряженности поля $~\Phi_ = \frac \Phi_$ . Для потока вектора напряженности электрического поля справедлива теорема Гаусса $~\Phi_ = \frac$ . Таким образом, сила тока между шариками выражается элементарно

Теперь легко вычислить искомое сопротивление

Задания для самостоятельной работы.

В каком месте при выводе формулы (8) мы учли, что ток идет между шариками?
Получите более точную формулу для сопротивления между шариками с учетом расстояния между ними (не полагая его бесконечно большим).

Теперь, внимание! Сравним два результата, формулы (5) и (8) – сопротивления, рассчитанные по этим формулам, отличаются в два раза, хотя, и в одном и другом случае рассматривается стекание тока с металлического шарика в неограниченную среду. Причина такого существенного расхождения заключается в различной структуре поля электрических токов – если в первом случае ток растекается радиально, одинаково во все стороны, то во втором ток преимущественно направлен в одну сторону, ко второму шарику. Тем самым, мы наглядно продемонстрировали, что электрическое сопротивление зависит не только от свойств среды и размеров источника, но и распределением токов.

Два одинаковых металлических шарика радиуса r

2017-10-13 Два одинаковых металлических шарика радиуса $R$ находятся на большом по сравнению с их размерами расстоянии $r$ друг от друга. Один из шариков имеет заряд $q$, другой не заряжен. Шарики соединяют на некоторое время проводником ничтожно малой емкости, в результате чего заряд q распределяется между ними поровну: $q_ = q_ = q/2$. Теперь оба шарика заряжены и энергия их взаимодействия

Объяснить возникающий парадокс: до соединения один из шариков не был заряжен, и, следовательно, энергия их взаимодействия была равна нулю. После соединения шариков, как видно из формулы (1), энергия их взаимодействия стала положительной, т. е. увеличилась. Откуда взялась эта энергия?

Из закона сохранения энергии следует, что электростатическая энергия шариков могла только уменьшиться. В самом деле, при соединении шариков и перетекании заряда в соединительном проводнике выделяется теплота. При соединении могла проскочить искра, что неизбежно связано с превращением электрической энергии в другие виды энергии. Возникающее противоречие с законом сохранения энергии может означать только то, что в приведенных в условии задачи рассуждениях что-то не учтено. Что же именно?

Рассмотрим уединенное заряженное тело. Его собственная энергия не зависит от того, каким способом оно было заряжено. Поэтому рассмотрим такой процесс зарядки, для которого легче всего сосчитать работу внешних сил. Пусть Заряд переносится на тело настолько малыми порциями $\Delta q^< \prime>$, что влиянием поля малого заряда на распределение уже сообщенного телу заряда можно пренебречь. Тогда работа $\Delta A$, совершаемая при перемещении $ \Delta q^< \prime>$ из бесконечности на тело, равна произведению переносимого заряда $\Delta q^< \prime>$ на потенциал тела $\phi^< \prime>$. Потенциал металлического тела в любой момент связан с находящимся на нем зарядом $q^< \prime>$ соотношением $\phi^ < \prime>= q^ < \prime>/ C$, где $C$ — емкость уединенного тела.

Поэтому для работы $\Delta A$ получаем

Суммируя работы $\Delta A$ по переносу всех порций заряда $\Delta q^< \prime>$, пока заряд тела не станет равен $q$, получаем для собственной энергии выражение

Емкость уединенного металлического шара радиуса $R$ равна $4 \pi \epsilon_ R$, поэтому собственная энергия такого шара, имеющего заряд $q$, дается выражением

Возвратимся теперь к рассматриваемому парадоксу. В начальном состоянии, когда энергия взаимодействия шариков равна нулю, система все-таки обладает электростатической энергией, которая равна собственной энергии заряженного шарика. Эта энергия дается формулой (4). В конечном состоянии, после соединения шариков, электростатическая энергия системы складывается из энергии их взаимодействия, выражаемой формулой (1), и собственных энергий каждого из шариков. Поскольку шарики находятся на большом расстоянии друг от друга, то можно считать, что заряды распределены на них равномерно. Это значит, что собственная энергия каждого из них определяется таким же выражением, как и для уединенного шара. Заряды шариков теперь равны $q/2$, поэтому для полной электростатической энергии системы в конечном состоянии имеем

Сравнивая выражения (4) и (5), видим, что полная электростатическая энергия системы в результате соединения шариков уменьшилась:

так как $r > R$. Разность $W_ - W^< \prime>$ равна количеству электростатической энергии, которая перешла в другие виды энергии при соединении шариков.

Итак, полная электростатическая энергия системы заряженных тел складывается из их собственных энергий н энергии их взаимодействия. Такое разбиение энергии становится особенно наглядным, если электростатическую энергию системы рассматривать как энергию электрического поля. По принципу суперпозиции электрическое поле $\vec$ системы двух тел с зарядами $q_$ и $q_$ равно векторной сумме полей $\vec_$ и $\vec_$, создаваемых каждым из тел в отдельности. Объемная плотность энергии электрического поля, пропорциональная квадрату напряженности, распадается на три слагаемых в соответствии с выражением

Первые два слагаемых в правой части соответствуют объемной плотности собственных энергий зарядов $q_$ и $q_$, а третье слагаемое соответствует энергии взаимодействия этих зарядов друг с другом. Именно эта часть полной электростатической энергии системы и дается формулой (1). Если бы, решая задачу о соединении шариков, мы с самого начала рассматривали электростатическую энергию системы как энергию электрического поля, то парадокса вообще не возникло бы.

Подведем итоги. Системе заряженных тел можно поставить в соответствие либо полную энергию — энергию электрического поля, либо энергию взаимодействия тел-Какому из этих способов отдать предпочтение при решении конкретных задач?

При всех возможных перемещениях заряженных тел, если распределение зарядов на них не меняется, собственная энергия этих тел остается неизменной. Поэтому при таких перемещениях изменение полной электростатической энергии равно изменению энергии взаимодействия. Так как во всех физических явлениях существенно именно изменение энергии системы, то постоянная часть — собственная энергия - может быть отброшена. Именно в этом смысле следует понимать часто встречающееся утверждение об эквивалентности энергии взаимодействия зарядов и энергии создаваемого ими поля.

Представление электростатической энергии как энергии взаимодействия зарядов особенно удобно в тех случаях, когда в рассматриваемую систему входят точечные заряды. Дело в том, что собственная энергия истинно точечного заряда бесконечна. Это видно, например, из формулы (4), если в ней, сохраняя заряд $q$ неизменным, устремить радиус шара $R$ к нулю. С другой стороны, это бесконечное значение собственной энергии точечного заряда остается строго неизменным при любых его перемещениях, и его можно отбросить при вычислении изменения энергии. Таким образом, то обстоятельство, что формула (1) не содержит собственной энергии зарядов, является ее достоинством, а вовсе не недостатком. Формула, содержащая собственную энергию, для системы, в которой есть точечные заряды, была бы лишена смысла.

В отличие от точечных зарядов, собственная энергия проводящих тел не остается неизменной. Она может измениться, например, при перетекании заряда с одного проводника на другой, как это было выяснено в разобранной задаче. Собственная энергия проводника может измениться и просто при взаимном перемещении входящих в систему тел. Действительно, собственная энергия незаряженного проводника равна нулю, если поблизости нет других заряженных тел. Но при приближении к проводнику точечного заряда $q$ на поверхности проводника возникают индуцированные заряды. Хотя полный заряд изолированного проводника равен нулю, перераспределение зарядов на его поверхности приводит к появлению электрического поля, создаваемого этими индуцированными зарядами. Это поле обладает энергией, и поэтому собственная энергия проводника уже отлична от нуля.

Разумеется, вывод о том, что собственная энергия проводников не остается постоянной при изменении взаимного расположения или величины зарядов окружающих тел, справедлив и для проводников, полный заряд которых отличен от нуля, так как и в этом случае происходит перераспределение зарядов по поверхности проводников.

Слободянюк А.И. Физика 10/11.8

§ 1.28. Примеры решения задач

Электрическая емкость — последняя тема главы «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: сохранение электрического заряда, понятия напряженности поля и потенциала, поведение проводников в электростатическом поле, изменение напряженности поля в диэлектриках, закон сохранения энергии применительно к электростатическим явлениям. Только при хорошем усвоении всех основных понятий электростатики решение задач на электрическую емкость не вызовет особых затруднений.

Основными формулами при решении задач на емкость являются следующие: формула (1.24.2) — определение емкости, формула (1.24.3) — емкость уединенного шара, выражения для емкости плоского конденсатора (1.25.3) и сферического конденсатора (1.25.7), а также формулы для определения емкости батареи конденсаторов при последовательном и параллельном их соединении (1.26.4) и (1.26.2).

Надо знать еще формулы (1.27.3) и (1.27.9) для энергии заряженного конденсатора и заряженного уединенного тела.

Задача 1

Два одинаковых металлических шарика радиусом г расположены в вакууме на расстоянии d друг от друга, причем d >> r. Шарики заряжены одинаковыми по модулю и противоположными по знаку зарядами. Какова электрическая емкость системы, образованной шариками?

Решение. Искомая емкость равна отношению заряда q одного из шариков к разности потенциалов между ними:

Найдем U. Потенциал φ₁ первого шарика, несущего заряд +q, складывается из его собственного потенциала : (см. задачу 16 § 1.23).

Аналогично потенциал второго шарика

Отсюда разность потенциалов

Поскольку d >> r, то с большой степенью точности можно считать, что

Задача 2

Найдите емкость С конденсатора, площадь пластин которого S и расстояние между ними l, если в конденсатор вставлена металлическая пластина толщиной d, параллельная его обкладкам (рис. 1.107).

Решение. Конденсатор со вставленной в него пластиной можно рассматривать как два последовательно соединенных конденсатора. Емкость первого из них . При последовательном соединении электрическая емкость батареи определяется уравнением:

Емкость не зависит от положения пластины. При очень тонкой пластине (d ⇒ 0) емкость конденсатора не зависит от наличия пластины.

Задача 3

В плоский конденсатор с расстоянием d между обкладками вводится диэлектрическая пластина, толщина которой d₁ < d.

Определите емкость конденсатора с диэлектрической пластиной. Диэлектрическая проницаемость материала пластины ε. Площадь пластины и каждой обкладки конденсатора S.

Решение. Если в плоский конденсатор внести очень тонкую проводящую пластину, параллельную обкладкам, то на ее поверхностях появятся заряды противоположных знаков, равные по модулю. При этом емкость конденсатора не изменяется (см. задачу 2). Поэтому можно считать, что на поверхностях диэлектрической пластины нанесены тонкие проводящие слои. В этом случае образуются три последовательно соединенных конденсатора с емкостями

где d₂ и d₃ — расстояния между поверхностями диэлектрической пластины и обкладками, причем d₂ + d₂ = d - d₁ (рис. 1.108).

Емкость С батареи из трех конденсаторов определяется из формулы

Задача 4

Ha рисунке 1.109 изображена батарея конденсаторов. Их емкости равны С₁ = C, C₂ = 2С, C₃ = ЗС, С₄ = 6С. Изменится ли емкость батареи, если между точками А и В включить конденсатор с емкостью C₅ = 8С?

Решение. Обозначим потенциалы на зажимах батареи φ₁ и φ₂, а в точках А и В соответственно φ₃ и φ₄.

Так как конденсаторы С1 и СЗ соединены последовательно, то их заряды одинаковы, т.е.

Разделив почленно равенство (1.28.1) на равенство (1.28.2) и учитывая, что, согласно условию задачи,

Отсюда найдем, что φ₃ = φ₄. т. е. точки А и В имеют одинаковые потенциалы. Поэтому если включить какой-либо конденсатор между точками А и В (рис. 1.110), то он не зарядится и, следовательно, не повлияет на емкость системы.

Схема, подобная схеме, изображенной на рисунке 1.110, называется мостовой. Конденсаторы С1 и С2, СЗ и С4 называются плечами моста. Обратите внимание, что если емкости плеч моста пропорциональны , то точки А и В имеют одинаковые потенциалы. Конденсатор С5 не заряжается, и его из схемы можно удалить (см. рис. 1.109).

Задача 5

Найдите емкость батареи конденсаторов, изображенной на рисунке 1.111. Емкость каждого конденсатора равна С.

Решение. Данная схема соединения конденсаторов эквивалентна схеме, изображенной на рисунке 1.112. В этом можно убедиться, проверив, что каждый из конденсаторов соединен с источником и с другими конденсаторами точно так же, как в исходной схеме.

Вследствие равенства емкостей всех конденсаторов разность потенциалов между точками А и В равна нулю. Поэтому конденсатор 4 можно исключить (см. задачу 4). В результате получится схема, изображенная на рисунке 1.113. Она состоит из трех параллельных ветвей, две из которых содержат по два последовательно включенных конденсатора.

Общая емкость системы

Задача 6

Два маленьких шарика радиусом г несут заряды q₁ и q₂, различные по модулю, но одинаковые по знаку. Шарики первоначально находятся на расстоянии l друг от друга. Один из шариков закреплен. Второй шарик, удаляясь под действием электростатических сил, приобретает максимальную кинетическую энергию W_k1. Если перед началом движения второго шарика оба шарика на некоторое время были соединены проводником, то второй шарик, удаляясь, приобретает максимальную кинетическую энергию W_k2 > W_k1. Определите количество теплоты, выделившееся в проводнике при соединении шариков, и выясните, за счет какой энергии выделяется эта теплота и увеличивается кинетическая энергия второго шарика.

Решение. Согласно закрну сохранения энергии в первом случае

где W_k01 и W_p01 + W_0c — начальные, a W_k1 и W_p1 + W_1c — конечные значения кинетической и потенциальной энергий системы двух шариков. Причем W_p01 и W_1c, — потенциальные энергии взаимодействия шариков, а W_0c и W_1c — их суммарные собственные энергии, одинаковые по модулю. Считая потенциальную энергию взаимодействия при бесконечно большом расстоянии между шариками равной нулю и учитывая, что W_k01 = 0, получим:

После соединения проводником заряды шариков становят-ся одинаковыми и равными

Нетрудно видеть, что действительно W_k2 > W_k1. Кроме того, в проводнике выделяется количество теплоты Q. Однако, разумеется, полная энергия должна сохраняться. Увеличение кинетической энергии и выделение теплоты во втором случае происходит за счет уменьшения собственной потенциальной энергии заряженных шариков при их соединении.

С учетом собственной энергии шариков конечную энергию в первом случае можно представить в виде

— собственная энергия шариков. Конечную энергию во втором случае запишем так:

Количество выделенной теплоты равно:

Упражнение 4

1. Пластины заряженного конденсатора попеременно заземляются. Будет ли при этом конденсатор разряжаться?

2. Плоский конденсатор, расстояние между обкладками которого d₁ = 10 мм, зарядили до разности потенциалов U₁ = 100 В, а затем отключили от сети. Определите разность потенциалов U₂ между обкладками конденсатора, если их раздвинули до расстояния d₂ = 20 мм.

3. Определите емкость конденсатора, площадь пластин которого равна S, а расстояние между пластинами d, если пластины погружены вертикально в жидкий диэлектрик до середины. Диэлектрическая проницаемость диэлектрика равна е.

4. В конденсатор емкостью C₀ внесли диэлектрическую пластинку с диэлектрической проницаемостью ε = 2. Пластинку расположили так, как указано на рисунке 1.114. Определите, во сколько раз изменилась емкость конденсатора при внесении в него пластинки. Площадь пластинки в 2 раза меньше площади обкладки конденсатора, а ее толщина в 2 раза меньше расстояния между обкладками.

5. Плоский конденсатор, пространство между пластинами которого заполнено керосином (ε = 2), расположен вертикально, заряжен и отключен от источника напряжения. Напряженность электрического поля при этом в керосине Е = 20 кВ/см. Из-за дефекта в корпусе конденсатора керосин начинает вытекать, а его место занимает воздух. Предельная напряженность электрического поля в воздухе, при которой наступает электрический пробой (разряд), Е_пр = 30 кВ/см. Какая доля δ керосина вытечет из конденсатора к моменту пробоя конденсатора?

6. Оцените приближенно электрическую емкость тела человека.

7. Найдите емкость металлического шара радиусом r, окруженного прилегающим концентрическим слоем диэлектрика с внешним радиусом R и диэлектрической проницаемостью ε.

8. К пластинам плоского конденсатора, находящимся на расстоянии d = 1 см друг от друга, приложена разность потенциалов U = 300 В. В пространство между пластинами помещается плоскопараллельная пластина из стекла толщиной d₁ = 0,3 см и плоскопараллельная пластина из парафина толщиной d₂ = 0,7 см. Найдите напряжения между поверхностями стеклянной и парафиновой пластин. Диэлектрические проницаемости стекла и парафина соответственно равны ε₁ = б и ε₂ = 2,6.

9. Определите емкость конденсатора с трехслойным диэлектриком, диэлектрические проницаемости слоев равны ε₁, ε₂, ε₁ (рис. 1.115). Толщина каждого диэлектрика (слоя) равна d. Площадь пластин S.

10. Четыре одинаковые металлические пластины расположены в воздухе на равных расстояниях d друг от друга (d мало по сравнению с размерами пластин). Площадь каждой из пластин равна S. Пластина 1 соединена проводником с пластиной 3, а от пластин 2 и 4 сделаны выводы (рис. 1.116). Определите емкость С такого конденсатора.

11. Определите емкость С батареи конденсаторов, схематически изображенной на рисунке 1.117. У каждого конденсатора указано значение его емкости, выраженное в микрофарадах.

12. Из проволоки сделан куб, в каждое ребро которого включено по одному конденсатору емкостью С (рис. 1.118). Найдите емкость получившейся батареи конденсаторов, если она включается в цепь проводниками, присоединенными к вершинам А и В куба.

13. Имеется N точек в пространстве. Между каждой парой точек включен конденсатор емкостью С. Найдите емкость образовавшейся батареи конденсаторов, если она включается в цепь выводами, присоединенными к двум произвольным точкам.

14. Плоский конденсатор емкостью С = 15 пФ зарядили до разности потенциалов U = 100 В, затем отключили от источника и погрузили полностью в жидкий диэлектрик (ε = 1,5). Определите изменение энергии конденсатора ΔW_p.

15. Три конденсатора емкостью С = 1 мкФ каждый соединены последовательно. Конденсаторы зарядили и отключили от источника. Заряд этой батареи q = 10 -4 Кл. Затем пространство между обкладками одного из конденсаторов заполнили диэлектриком с диэлектрической проницаемостью ε = 2. Найдите энергию, запасенную в электрическом поле этих конденсаторов, и напряжение на зажимах батареи после заполнения диэлектриком одного из конденсаторов.

16. Энергия заряженного плоского конденсатора, заполненного диэлектриком, равна W_p = 2 • 10 -5 Дж. После отключения конденсатора от источника напряжения диэлектрик из конденсатора вынули, совершив при этом работу А = 7 • 10 -5 Дж. Найдите диэлектрическую проницаемость диэлектрика.

17. Сделаем в пластинах плоского конденсатора два малых отверстия — одно напротив другого. Пусть через одно из отверстий в заряженный конденсатор влетает с небольшой начальной скоростью частица так, чтобы электрическое поле конденсатора ускоряло ее (рис. 1.119).

Пролетев через конденсатор, частица вылетает из другого отверстия, приобретая дополнительную энергию ΔW_p = qU, где q — заряд частицы, а U — разность потенциалов на пластинах конденсатора. Теперь с помощью магнитного поля направление движения частицы изменяется таким образом, чтобы она снова влетела через первое отверстие в конденсатор (см. рис. 1.119). (В главе 4 вы узнаете, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, не совершает работы.) При повторном пролете через конденсатор частица вновь приобретает дополнительную энергию ΔW_p, в следующем цикле — еще ΔW_p и т. д. Получается циклический ускоритель, который не нуждается в источнике энергии! Где ошибка в приведенных рассуждениях?

18. Два конденсатора емкостью С₁ и C₂ заряжены до разности потенциалов U₁ и U₂ (U₁ ≠ U₂). Докажите, что при параллельном соединении этих конденсаторов их общая энергия уменьшается. Объясните, почему происходит уменьшение энергии.

19. Две прямоугольные пластины длиной l и площадью S расположены параллельно друг другу на расстоянии d (плоский конденсатор). Пластины заряжены до разности потенциалов U. В пространство между пластинами втягивается диэлектрик с диэлектрической проницаемостью ε. Толщина диэлектрика равна d, его ширина равна ширине пластин, а длина больше l (рис. 1.120). Трение отсутствует. Найдите зависимость силы, действующей на диэлектрик со стороны поля, от расстояния х.

20. Решите задачу 19 при условии, что разность потенциалов между пластинами поддерживается постоянной и равной U.

Мы потратили довольно много времени на изучение электричества, а рассмотрели лишь простейший частный случай неподвижных заряженных тел — электростатику. Может быть, не стоило уделять электростатике такое больпюе внимание? Нет, стоило! Мы ввели важнейшие понятия, используемые во всей электродинамике: «электрический заряд», «электрическое поле», «потенциал» и «разность потенциалов», «электрическая емкость», «энергия электрического поля». На простом частном случае выяснить суть этих фундаментальных понятий не так трудно, как в общем случае движущихся зарядов.

Теперь перейдем к изучению электромагнитных процессов, наблюдаемых при движении заряженных частиц.

Читайте также: