Получите формулу энергии поля заряженного металлического шара

Обновлено: 02.05.2024

Рассмотрим сначала уединенный проводник, находящийся достаточно далеко от других тел. Если этому проводнику сообщить заряды после их перераспределения по объему проводника он приобретает потенциалы Отношение для данного уединенного проводника оказывается постоянным, зависящим только от его формы и размеров, и называется его электроемкостью. Это отношение сохраняется и при бесконечно малых изменениях заряда и потенциала, так что

Понятие электроемкости применимо только к проводникам, так как для них существует равновесное распределение зарядов по объему тела, при котором все точки проводника имеют один и тот же потенциал. Если же заряд сообщается изолятору, то он не растекается по нему и поэтому в различных местах изолятора потенциал может быть различен (в зависимости от расстояний до того места, где находится подведенный заряд).

Емкость уединенного шара радиуса находящегося в безграничном диэлектрике с проницаемостью легко рассчитать, так как потенциал на его поверхности (а следовательно, и в любой точке его объема)

При наличии вблизи данного проводника других тел — проводников или изоляторов — отношение (1.58) зависит также от формы, размеров и относительного расположения соседних тел. Если эти соседние тела — проводники, то в них происходит перераспределение свободных зарядов, электрическое поле которых накладывается на поле данного тела и изменяет его потенциал. Если же соседние тела — диэлектрики, то они поляризуются, вследствие чего на поле данного тела накладывается поле связанных зарядов диэлектрика; это опять-таки изменяет потенциал рассматриваемого проводника.

разности потенциалов между обкладками:

Допустим, что расстояние между обкладками настолько мало, что электрическое поле между ними можно считать однородным; напряженность этого поля, согласно формуле (1.36),

где площадь обкладок; поверхностная плотность зарядов на обкладках. Для однородного поля выполняется соотношение (1.45), поэтому

Подставив это выражение в формулу (1.60), получаем формулу Для расчета емкости плоского (двухпластинчатого) конденсатора:

У шарового конденсатора потенциалы на обкладках определяются зарядами которые имеются на этих обкладках, и их радиусами и

поэтому формула для расчета емкости такого конденсатора имеет вид

где величина зазора между обкладками. Если радиусы обкладок очень велики и мало, то можно положить (площадь обкладок) и тогда полученная формула будет совпадать с (1.61).

У цилиндрического конденсатора определяется емкость, приходящаяся на единицу длины. Выведем сначала формулу для разности потенциалов между обкладками; согласно формулам (1.32), (1.13) и (1.39), имеем:

(Интегрирование ведем вдоль перпендикуляра к оси конденсатора, т. е. вдоль направления силовой линии вектора очень длинного цилиндрического конденсатора вектор напряженности поля в зазоре перпендикулярен оси конденсатора: это условие не соблюдается на концах, но этим обстоятельством для достаточно длинных конденсаторов можно пренебречь.) Так как на единице длины каждой обкладки имеется заряд то «погонная» емкость цилиндрического конденсатора будет равна

Если величина зазора очень мала, то По этой формуле рассчитываетсямкость электрического кабеля, состоящего из внутреннего провода и наружной металлической брони, между которыми находится слой диэлектрика.

В электротехнике приходится рассчитывать емкость двухпроводной линии — системы из двух параллельных проводов (обычно круглого сечения). Обозначим

диусы сечений этих проводов через расстояние между осями проводов — через а и допустим, что . В этомслучае поле вокруг каждого провода можно с удовлетворительным приближением рассчитывать по формуле (1.34). Допустим, что на единице длины одного провода находится заряд а другого . В некоторой точке, расположенной на расстоянии х от оси первого провода, суммарная напряженность поля будет равна

Интегрируя вдоль перпендикуляра, соединяющего оси проводников, получим разность потенциалов между проводами:

Следовательно, погонная емкость двухпроводной линии будет равна

Так как было предположено, что расстояние между проводами значительно больше радиуса их сечений, то

В приведенных выше расчетных формулах для электроемкости при использовании системы следует положить а в Международной системе В частности, для плоского конденсатора:

Электроемкость выражается в фарадах В системе единицей электроемкости является сактиметр:

Так как заряда, потенциала, то см.

Рассмотрим параллельное (рис. II 1.26, а) и последовательное (рис. III.26, б) соединения конденсаторов. Если к точкам параллельно соединенных конденсаторов подвести равные и противоположные заряды то они распределятся между обкладками конденсаторов так, что Разность же потенциалов между обкладками всех конденсаторов будет одна и та же (так как они соединены вместе проводниками); обозначим через Емкостью такой системы конденсаторов называется отношение

Однако отношение емкость первого конденсатора, емкость второго и т. д. Следовательно,

Можно показать, что обычный многопластинчатый плоский конденсатор с числом пластин представляет собой параллельное соединение плоских двухпластинчатых конденсаторов, поэтому

Если к точкам последовательно соединенных конденсаторов подвести заряды то вследствие электростатической индукции на обкладках конденсаторов появятся равные и противоположные по знаку заряды При этом пластинки соседних конденсаторов, соединенные между собой проводником, имеют одинаковый потенциал.

Так как разность потенциалов на концах любой линии равна сумме разностей потенциалов на отдельных участках этой линии, то для линии проходящей через электрические поля соединенных конденсаторов, можно написать:

Емкостью этой системы конденсаторов по-прежнему называется отношение

Так как для первого конденсатора для второго то

Заметим интересную деталь: если между обкладками плоского конденсатора поместить несколько металлических пластинок, расположенных параллельно обкладкам (т. е. вдоль эквипотенциальных поверхностей), и если суммарный зазор между ними равен первоначальному зазору то емкость конденсатора не изменится. Действительно, такой конденсатор можно рассматривать как систему последовательно соединенных плоских конденсаторов, поэтому, применив формулу (1.64) и (1.67), получим

т. е. первоначальная емкость конденсатора не изменилась. В частности, емкость конденсатора не изменится, если вдоль эквипотенциальных поверхностей поместить металлические пластинки бесконечно малой толщины.

Если между обкладками плоского конденсатора имеются различные диэлектрики, как это показано на рис. II 1.26, в, а, то для расчета емкости такого конденсатора можно воспользоваться формулами (1.65) и (1.67). Конденсатор (рис. II 1.26, в) можно представить как систему из параллельно соединенных конденсаторов, имеющих одинаковые расстояния между пластинами, но различные и , и тогда

Конденсатор (рис. II 1.26, г) можно представить как систему последовательно соединенных плоских конденсаторов; так как введение или удаление бесконечно тонких металлических пластинок, параллельных обкладкам, не изменяет емкости конденсатора, то эти пластинки можно расположить вдоль границ между диэлектриками. Тогда, воспользовавшись формулами (1.61) и (1.67), получим

Если то эта формула перейдет в (1.61).

Для того чтобы сообщить проводнику некоторый заряд необходимо затратить определенную работу, так как каждая последующая порция подводимого заряда испытывает отталкивающее действие ранее поступивших на проводник одноименных зарядов. Допустим, что очередная порция заряда подводится из бесконечности, где потенциал к проводнику, имеющему уже потенциал Тогда элементарная работа, затрачиваемая на подведение заряда

Это выражение для работы можно видоизменить, если воспользоваться соотношением

Знак минус указывает, что для зарядки тела необходимо совершить некоторую внешнюю работу А. При разрядке электрическое поле заряженного тела само совершает работу, равную Таким образом, формула

выражает энергию заряженного проводника. Аналогичная формула получается и для заряженного конденсатора, причем означает разность потенциалов между клеммами конденсатора (или системы конденсаторов).

Энергию плоского конденсатора можно выразить через напряженность поля между обкладками. Подставим в формулу (1.68), тогда

Произведение выражает объем электрического поля между обкладками конденсатора, а отношение которое обозначим через есть энергия конденсатора, приходящаяся на единицу объема его электрического поля:

Полагая, что энергия заряженных тел есть энергия их электрического поля, величину можно назвать объемной плотностью энергии электрического поля.

Заметим, что постоянную принято выражать не в

Воспользуемся формулой для плотности энергии электрического поля и рассчитаем энергию, которая содержится в электрическом поле заряженного шара радиуса . В тонком слое, ограниченном сферами радиусов будет содержаться энергия Если заряд шара равен как напряженность поля на расстоянии от центра шара равна то

Эта формула показывает, что энергия электрического поля заряженного шара в основном сосредоточена вблизи его поверхности. Действительно, в шаровом слое, ограниченном поверхностью шара и сферой радиуса содержится столько же энергии, сколько имеется в остальном пространстве от до бесконечности:

Два заряженных шара при одинаковом заряде имеют в окружающем их электрическом поле различную энергию; чем меньше радиус шара, тем больше эта энергия. Для точечного заряда энергия электрического поля была бы бесконечно большой.

ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ

Пусть имеются два неподвижных точечных заряда (рис.16.1). Поле - электростатическое и потенциальное, силы консервативны. Работа, которую совершает поле заряда q₁ при переносе заряда q₂ из бесконечности в точку 2 в соответствии с (6.3) и (6.16) равна

Считая, что W_{p ¥} (r_{1 ¥}®¥ )=0, получаем

Это энергия взаимодействия двух точечных зарядов, которая в зависимости от знака зарядов, может быть как положительной, так и отрицательной. Можно говорить, что заряд q₂ в поле, созданном зарядом q₁ обладает потенциальной энергией W_p. Из симметрии формулы ясно, что можно рассуждать и наоборот.

Теперь добавим в систему третий заряд q₃ (рис.16.2). По аналогии

а энергия всей системы зарядов

Заметим, что в это выражение все величины входят симметрично, т.е. безразлично, в какой последовательности мы собирали систему. Эта энергия не зависит от процесса, а лишь от состояния системы. Потенциальная энергия - это функция состояния системы. Нулевое значение берется при бесконечном удалении зарядов друг от друга. Заметим также, что это энергия всей системы, энергия взаимодействия, поэтому бессмысленно говорить, что какая-то часть этой энергии принадлежит одному из зарядов. Здесь мы не учитываем собственную энергию каждого точечного заряда.

Это та энергия, которую нужно затратить, чтобы собрать из бесконечно малых порций заряда точечный заряд. Формально она бесконечна, так как необходимо уложить заряды в нулевой объем. Кроме того, эту энергию изменить весьма проблематично. Поэтому можно считать, что это постоянная величина. А мы помним, что потенциальную энергию определяют с точностью до постоянной, которую всегда можно отбросить, так как смысл имеет не сама энергия, а ее изменение.

Обобщив сказанное, можно записать потенциальную энергию взаимодействия системы из N точечных зарядов

Множитель 1/2 появляется в связи с тем, что при суммировании каждая пара зарядов входит в формулу два раза. Перепишем это выражение несколько по иному

где j _i - потенциал в точке, где находится заряд q_i, созданный всеми другими зарядами.

Напомним, что энергия одного точечного заряда в поле, созданном всеми другими зарядами (рис.16.2) вычисляется в соответствии с формулами (6.16)-(6.18) как

2. Энергия заряженного тела.

Если распределение зарядов в пространстве непрерывное, то

Эту формулу уже можно трактовать и по-другому. При конечных размерах тела потенциал в любой точке пространства конечен в отличии от точечного заряда. Поэтому эту формулу можно рассматривать и как учитывающую собственную энергию заряда, то есть энергию, которую нужно было затратить, чтобы собрать этот заряд из бесконечно малых частей.

Заметим, что полная энергия (16.8) всегда положительна. При переходе к точечным зарядам она становится бесконечной положительной величиной. Если от этой бесконечной величины отнять бесконечную собственную энергию точечных зарядов, то останется конечная энергия взаимодействия точечных зарядов друг с другом (16.6), которая может быть как положительной, так и отрицательной.

Формула (16.7) соответствует духу теории дальнодействия, так как выражает энергию через потенциалы и заряды тел.

3. Энергия заряженной сферы.

Для примера рассчитаем энергию сферы с зарядом Q и радиусом R. Сначала запишем ее объемную плотность заряда как r =A d (r-R), где d - дельта-функция Дирака, а константу А найдем из очевидного соотношения

где dV=4 p r 2 dr. Очевидно, что - то есть поверхностная плотность заряда. Потенциал, который создает сфера, нам известен (7.17). Тогда энергия сферы в соответствии с (16.8)

Хотя потенциал сферы внутри и снаружи описывается разными формулами, но при вычислении необходимо только его значение на поверхности сферы, а там он одинаков.

4. Энергия конденсатора.

Известно, что если взять заряженный конденсатор и замкнуть его обкладки через сопротивление, то по цепи потечет ток, проводник нагреется, выделится какое-то количество теплоты. Следовательно, заряженный конденсатор обладал запасом энергии.

Перекидывая ключ на схеме (рис.16.3)(попробуйте это сделать движением мыши), можно периодически заряжать конденсатор от источника и разряжать его через резистор. Лампочка при этом будет на короткое время вспыхивать. Найдем выражение для энергии плоского конденсатора, используя (16.6). Нас очень выручит то, что поле между обкладками этого конденсатора однородно. Тогда

Оказывается, что это выражение справедливо для любого конденсатора. Кроме того, учтем, что часто используют понятие напряжения U, как модуля разности (или изменения) потенциалов. В электростатике это справедливо. Более подробно мы разберем понятие напряжения в лекции №18.

Учитывая вышесказанное и (15.3), энергию конденсатора можно записать как

Все три формы записи эквивалентны и применяются при решении задач в зависимости от того, какая из величин остается постоянной.

5. Энергия электрического поля.

Мы выяснили, что система точечных зарядов и конденсатор обладают энергией. Можно предположить, что это энергия самих зарядов, в том числе и расположенных на обкладках конденсатора. Однако можно говорить, что это энергия электрического поля, созданного системой зарядов или поля внутри конденсатора. Какая из этих точек зрения более правильная неясно. Ответ может дать только опыт, а в электростатике такой эксперимент невозможен, так как нет поля без зарядов, и зарядов без поля. Поэтому этот волнующий вопрос мы оставим без внимания до тех пор, пока не начнем изучать переменные поля.

Здесь выразим энергию конденсатора через характеристики поля, зная формулу емкости плоского конденсатора (15.6), связь между напряженностью и потенциалом (7.8), и очевидное выражение для объема V=Sd

Таким образом, энергия равна

Естественно, это справедливо, если нет сторонних потерь и диэлектрическая проницаемость постоянна. Однако нетрудно догадаться, как выглядит это выражение в произвольном случае для бесконечно малого объема.

Часто говорят об энергии единицы объема или о плотности энергии электростатического поля

Формула (16.30) соответствует духу теории близкодействия, так как выражает энергию через характеристики поля. Сравните с (16.8). Эти формулы эквивалентны.

rem: Если вы считаете, что усвоили данный материал, то попробуйте поразмышлять о следующем. Энергия конденсатора и поля в нем согласно (16.26) и (16.30) положительна, а энергия разноименно заряженных пластин по (16.5) отрицательна. Как вы объясните это противоречие?

6. Энергия заряженной сферы(еще раз).

Вновь вернемся к задаче о заряженной сфере. Добавим вокруг нее среду с диэлектрической проницаемостью e . Рассчитаем еще двумя способами ее энергию. Емкость ее известна (15.10), тогда по (16.26)

Теперь рассчитаем энергию поля, созданного этой сферой, не забыв о том, что внутри поля нет.

Как и ожидалось, результаты (16.24), (16.32) и (16.33) совпадают.

rem: Заметим, что потенциальная энергия подчиняется принципу минимума: в любой системе проводников при фиксированных значениях потенциалов заряд распределяется таким образом, чтобы энергия, запасенная во всем поле была минимальна.

7. Сила взаимодействия пластин конденсатора.

Ранее отмечалось, что для любого потенциального поля выполняется следующее соотношение между силой и энергией

Тогда несложно рассчитать силу взаимодействия между пластинами плоского конденсатора.

Через характеристики поля:

Следовательно, сила, приходящаяся на единицу площади пластин конденсатора, численно равна плотности энергии. Как и следовало ожидать это сила притяжения, так как пластины заряжены разноименно.

Через энергию конденсатора (16.26) расчет еще проще

Эта формула в точности совпадает с (12.10).

Заметим, что сила стремится уменьшить область пространства, заполненного электрическим полем, то есть уменьшить потенциальную энергию в соответствии с принципом минимума потенциальной энергии.

8. Классический радиус электрона.

Будем считать, что электрон - это маленький шарик с зарядом q=е, радиусом R и диэлектрической проницаемостью e ₁. Вокруг него среда с диэлектрической проницаемостью e ₂.

Снаружи шара все аналогично заряженной сфере, так как поля шара и сферы снаружи одинаковы. Тогда энергия поля снаружи равна

Внутри равномерно заряженного шара поле тоже известно (5.14), поэтому

Интеграл несложный. Мы легко получаем энергию поля внутри шара

Очевидно, что полная энергия заряженного шара

Согласно знаменитому соотношению Эйнштейна между массой и энергией

W=mc 2

где m- масса электрона, с- скорость света в вакууме. Приравнивая, получаем

На коэффициент в скобках не обращают внимания, так как непонятно, что такое диэлектрическая проницаемость среды внутри электрона. Ясно, что эта величина находится в диапазоне от 0,5 до 0,6, поэтому ее для оценки считают равной единице, и определяют классический радиус электрона по формуле

Расчет показывает, что эта величина равна

R_е=2,8179380 × 10 -15 м.

Вспомним, что радиус самого маленького атома водорода - первый боровский радиус R_b=0,529 × 10 -10 м , и убедимся, что атом в, основном, пуст, и напоминает солнечную систему в миниатюре.

9. Точечный заряд и бесконечная плоскость.

Вычислим энергию, которой обладает точечный заряд вблизи заземленной проводящей плоскости (см. лк.№10 п.1). Сила, действующая на заряд известна. Вычислим работу, совершаемую этой силой, при перемещении заряда в бесконечность. При бесконечном расстоянии энергия - 0.

теперь найдем ту же самую величину как энергию взаимодействия двух точечных зарядов: самого заряда и его зеркального отображения по формуле (16.2).

Результат получился в 2 раза больше?! Дело в том, что за плоскостью на самом деле поля нет, поэтому от полученного выражения нужно оставить только половину, что как раз и совпадает с (16.48).

10. Конденсатор с частичным заполнением-1.

В качестве дополнительной тренировки рассчитаем силу, действующую на единице поверхности диэлектрика, если заряженный конденсатор заполнен им не полностью, а частично. Конденсатор отключен от источника питания.

Сначала рассмотрим следующую конфигурацию (рис.16.6). Данный конденсатор можно рассматривать как два конденсатора, соединенных последовательно. Тогда их емкости соответственно

и , а общая емкость

Тогда в соответствии с (16.34)

Если e ₁< e ₂, то F_x. Если e ₁> e ₂, то F_x>0. Очевидно, что диэлектрик втягивается в область с меньшей диэлектрической проницаемостью. Направление силы легко было определить, как силу, действующую со стороны поля на поляризационный заряд. И, наконец, если конденсатор заполнится полностью диэлектриком с большей диэлектрической проницаемостью, то его энергия станет меньше в соответствии с принципом минимума.

Выразим формулу (16.54) через характеристики поля, учитывая, что Q= s S=DS. Заметим, что индукции по обе стороны от границы одинаковы. Тогда

Следовательно, сила, приходящаяся на единицу площади пластин конденсатора, численно равна разности плотности энергий

Сравните с (16.38) и вспомните, что снаружи конденсатора поля нет. Заметим только, что (16.38) - это сила, действующая на заряженную пластину (обкладку), а (16.57) - сила, действующая на поверхность диэлектрика. Они отличаются знаками, но по модулю равны, ведь третий закон Ньютона должен выполняться и здесь.

Эту же формулу можно получить быстрее, используя (16.30) и (16.31).

где V₁=Sx, V₂=S(d-x) - объемы областей, заполненных каждым диэлектриком. При смещении границы плотности энергии не меняются. После дифференцирования вновь получаем формулу (16.57).

11. Конденсатор с частичным заполнением-2.

Пусть теперь диэлектрик заполняет конденсатор по-другому (рис.16.7). Сторона пластины равна а. Очевидно, что такую систему можно рассмотреть как два параллельно соединенных конденсатора. Далее все делаем по аналогии с п.10 и получаем следующее выражение для силы

Опять видим, что сила направлена в сторону диэлектрика с меньшей диэлектрической проницаемостью. Учтем, что при этом распределение зарядов на пластинах конденсатора меняется. Однако напряженности поля справа и слева от границы равны.

Через характеристики поля сила, действующая на единицу поверхности, выражается следующим образом

Формулы (16.57) и (16.60) очень похожи.

Можно сделать общий вывод:

Lex: Сила, действующая на границу диэлектрика, пропорциональна разности плотностей энергии электростатического поля и направлена в сторону диэлектрика с меньшей диэлектрической проницаемостью.

Теперь мы легко можем рассчитать, на какую высоту поднимется жидкий диэлектрик между двумя заряженными пластинами (лк. №12 п.7 рис.12.11). Остановит подъем гидростатическое давление. Сверху над диэлектриком - вакуум. Тогда

отсюда высота подъема

Попробуйте решить ту же задачу, если конденсатор подключен к источнику питания. Результат должен быть аналогичен (16.60). Если ошибетесь со знаком, то посмотрите разъяснения Фейнмана (т.5 стр 158 и 213).

Слободянюк А.И. Физика 10/9.13

Вернемся к обсуждению вопроса об энергии взаимодействия электрических зарядов. Ранее мы показали, что потенциальная энергия электростатического взаимодействия двух точечных зарядов q₁ и q₂, находящихся на расстоянии r друг от друга (рис. 212), рассчитывается по формуле

Придадим этой формуле несколько иной вид

здесь \(~\varphi_1 = \frac \frac\) - потенциал поля, создаваемого вторым зарядом, в точке, где находится первый заряд. Аналогично можно записать

где \(~\varphi_2 = \frac \frac\) - потенциал поля, создаваемого первым зарядом, в точке, где находится второй заряд. Теперь, перепишем выражение (1), в симметричной форме, легко допускающей обобщение

\(~U(r) = \frac (q_1 \varphi_1 + q_2 \varphi_2)\) . (2)

В этой формуле мы выписали два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но мы подчеркивали, что энергия взаимодействия, не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды – из-за этого и появляется в формуле множитель 1/2.

Если система состоит из нескольких зарядов q₁, q₂, …, q_N , то полная энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов. Используя симметричное выражение (2), суммирование по парам зарядов (двойную сумму), можно заменить на суммирование по самим зарядам, то есть записать

В этой формуле φ_k - потенциал поля в точке, где находится заряд q_k, причем поля, создаваемого всеми зарядами, кроме самого заряда q_k (как говорят, исключая самовоздействие заряда на самого себя).

Использование понятия энергии взаимодействия требует чрезвычайной точности и внимательности. Произвол в выборе нулевого уровня энергии, с одной стороны, предоставляет определенную свободу, а, с другой, требует четкого понимания о какой именно энергии идет речь. Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Если же требуется рассчитать работу поля при изменении положения зарядов, то выбор нулевого уровня не принципиален – эта работа не зависит от нулевого уровня потенциала.

Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим примеры расчета энергии электростатического взаимодействия.

Три точечных заряда.

Пусть три одинаковых точечных заряда, величины которых равны между собой q₁ = q₂ = q₃ = q, расположены в вершинах правильного треугольника со стороной a (рис.213). Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен

\(~\varphi_1 = \varphi_2 = \varphi_3 = 2 \frac\) .

В соответствии с формулой (3) энергия взаимодействия зарядов равна

\(~U_0 = \frac (q_1 \varphi_1 + q_2 \varphi_2 + q_3 \varphi_3) = 3 \frac\) . (4)

Такую работу совершит электрическое поле, при удалении всех зарядов на бесконечное расстояние друг от друга.

Если заряды сместятся, так что окажутся в вершинах правильного треугольника со стороной a₁ , то их энергия окажется равной

При таком смещении работа электрического поля будет равна уменьшению энергии системы

Обратите внимание, при \(~a_1 \to \infty\) эта работа становится в точности равной начальной энергии U₀.

Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся (рис. 215), то энергия системы станет равной

При этом поле совершит работу

Если теперь удалить еще один заряд, то энергия системы станет равной нулю, при этом поле совершит работу A₂ = U₁. В итоге начальная энергия полностью расходуется на совершение полной работы U₀ = A₁ + A₂ .

Задание для самостоятельной работы.

Проанализируйте изменение энергии и совершенные работы в рассмотренной системе, если один из зарядов отрицательный.

Энергия взаимодействия двух равномерно заряженных параллельных пластин.

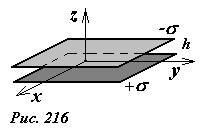
Найдем энергию взаимодействия двух равных по модулю зарядов противоположного знака, равномерно распределенными по двум параллельным пластинам. Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой -σ. Расстояние между пластинами h будем считать значительно меньшим размеров пластин, площадь каждой пластины обозначим S. Краевыми эффектами пренебрежем.

Для расчета энергии взаимодействия воспользуемся формулой U = qφ’, где φ’ - потенциал поля создаваемого всеми зарядами, кроме заряда q.

Напряженность поля между пластинами была вычислена нами ранее, она равна

Для «упрощения» расчетов положим потенциал отрицательно заряженной пластины равным нулю, тогда потенциал другой пластины будет равен

\(~\varphi = -\vec E \cdot \Delta \vec r = Eh = \frac\) . (6)

Здесь \(~\Delta \vec r\) - вектор перемещения от отрицательной пластины к положительной. Данная формула определяет потенциал поля, создаваемого зарядами на обеих пластинах.

Теперь необходимо найти потенциал поля φ’, создаваемого только одной пластиной. Напряженность поля E’, создаваемого одной пластиной в два раза меньше напряженности поля между пластинами \(~E' = \frac = \frac\) , поэтому искомый потенциал будет равен \(~\varphi' = E'h = \frac\) . Таким образом, энергия взаимодействия зарядов оказывается равной

здесь σS - заряд положительно заряженной пластины.

Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует. Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу, увеличивая энергию системы.

Энергию рассматриваемой системы можно найти, рассчитывая работу внешних сил, по разнесению пластин. На одну из пластин со стороны другой действует сила электрического притяжения \(~F = q E' = (\sigma S) \frac = \frac S\) , причем эта сила не зависит от расстояния между пластинами. Для того, чтобы раздвинуть пластины на расстояние h, необходимо приложить внешнюю силу, равную по модулю силе электрического притяжения (рис. 218). При этом эта сила совершит работу (равную увеличению энергии системы)

Таким образом, мы получаем ту же формулу для энергии систему зарядов. Используя соотношение между напряженностью поля между пластинами и поверхностной плотностью заряда σ = ε₀E, выразим энергию взаимодействия через напряженность поля

В процессе разнесения пластин создается электрическое поле во все большем объеме между пластинами, поэтому можно утверждать, что совершенная работа увеличивает энергию электрического поля, или работа расходуется на создание поля. Так при смещении пластины на расстояние Δz, объем занятый полем увеличивается на SΔz, если расстояние между пластинами увеличилось от нуля до некоторого значения h, то поле создается в объеме Sh. Таким образом, найденная энергия взаимодействия зарядов (7) есть энергия электрического поля - энергия «размазанная» по той области пространства, где создано поле. Косвенным подтверждением сделанного заключения, является тот факт, что энергия взаимодействия пропорциональна объему части пространства V = Sh, занятого полем и выражается через характеристику поля (его напряженность) – в формуле (8) нет характеристик зарядов. Электрическое поле, уже благодаря своему существованию обладает энергией. В качестве энергетической характеристики поля следует рассматривать энергию, содержащуюся в единице объема, то есть объемную плотность энергии\[~w = \frac\] . Из выражения (8) следует, что объемная плотность энергии электрического поля определяется формулой

Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке» требует предельного перехода: плотностью энергии электрического поля называется отношение энергии поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю

Энергия поля равномерно заряженной сферы.

Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R. Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле отсутствует. Так напряженность поля в точке, находящейся на расстоянии r от центра сферы равна

в частности непосредственно у поверхности сферы напряженность поля равна

Обратим внимание, что произведение \(~S = 4 \pi R^2\) есть площадь сферы, поэтому отношение \(~\frac = \sigma\) является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе \(~E_0 = \frac\). Потенциал поверхности сферы также был вычислен нами ранее

Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N равных малых частей (рис.220), величины которых равны \(~\delta Q_k = \frac\) (k = 1,2…N). Рассмотрим один из этих малых зарядов. В точке его расположения потенциал поля, создаваемого всеми остальными (N-1) зарядами равен \(~\varphi_k = \frac\). С использованием симметричной формулы \(~U = \frac \sum_ \) , выражение для энергии взаимодействия приобретает вид

данная сумма содержит N одинаковых слагаемых, поэтому равна

Так как число частей N, на которые разбивается сфера, может быть сделано сколь угодно большим, поэтому в пределе \(~N \to \infty\) слагаемое \(~\frac\) исчезает, поэтому окончательное выражение для энергии взаимодействия зарядов сферы имеет вид

Заметим, что полученное выражение имеет вид \(~U = \frac Q \varphi_0\). Если сразу заявить, что уменьшение заряда на малую величину \(~\delta Q\) пренебрежимо мало изменяет потенциал сферы, то результат (4) получается прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.

Приведем еще один вывод этой же формулы. Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда \(~\delta Q_k = \frac\) (k = 1,2…N), которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то перенесение первой «порции» заряда не требует совершения никакой работы. После того как сфера приобрела некоторый электрический заряд, перенесение следующей порции заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов сферы. Если на сферу перенесено (k-1) порций заряда, то ее потенциал равен \(~\varphi_ = \frac\) . Поэтому для того, что бы перенести на сферу следующую порцию заряда необходимо совершить работу

Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.

Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии

Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при бесконечном уменьшении порций переносимых зарядов (\(~N \to \infty\)) мы опять приходим к формуле (14).

В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы собрать их обратно.

Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR, а ее заряд при этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом уменьшится. В пространстве вне сферы увеличенного радиуса электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами – исчезло (рис. 221). Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя \(~\Delta V = 4 \pi R^2 \Delta R\) . Пренебрегая изменением напряженности поля в пределах тонкого слоя, энергию, заключенную в нем запишем в виде

\(~\Delta U = w \Delta V = 4 \pi R^2 \Delta R w\) , (16)

где w - плотность энергии поля. С другой стороны эта энергия равна изменению энергии взаимодействия зарядов при увеличении радиуса сферы

На последнем шаге, мы пренебрегли малым изменением радиуса ΔR. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности \(~Q = 4 \pi \varepsilon_0 R^2 E\) :

Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой \(~w = \frac\).

Слободянюк А.И. Физика 10/10.3

§10. Проводники и диэлектрики в электростатическом поле

10.3 Применение электростатических свойств проводников.

Приведем некоторые примеры использования рассмотренных свойств поведения проводников в электрическом поле.

Электростатическая защита.

Иногда возникает необходимость изолировать некоторые тела, приборы от воздействия внешних электрических полей. Для такой изоляции их помещают внутрь металлического корпуса. Мы показали, что при помещении проводника во внешнее электрическое поле, индуцированные заряды возникают только на поверхности проводника, а поле внутри проводника оказывается равным нулю.

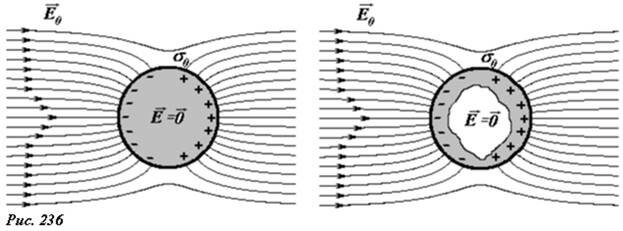
Пусть, например, металлический шар помещен в однородное электрическое поле напряженностью \(~\vec E_0\) (рис. 236). Под действием этого поля на поверхности шара возникнут индуцированные заряды, поверхностная плотность которых σ₀, будет различна в различных точках поверхности шара. Эти заряды приведут к изменению электрического поля: внутри шара напряженность поля станет равной нулю, снаружи – силовые линии поля будут перпендикулярны поверхности шара. Если теперь внутри шара вырезать произвольную полость, то от этой «операции» распределение поля и индуцированных зарядов не изменится, так как изъята та часть шара, где нет ни зарядов, ни поля. Аналогичные рассуждения можно распространить на произвольную полость внутри проводящего тела произвольной формы, находящегося в произвольном электростатическом поле – в любом случае поле внутри полости будет отсутствовать. Говорят, что проводящая оболочка экранирует внешнее электрическое поле.

Более того, можно показать, что аналогичного эффекта достигается даже в том случае, если сплошную проводящую оболочку заменить на металлическую сетку с мелкими ячейками. В этом случае электрическое поле проникает за сетку на глубину порядка размеров ячейки сетки.

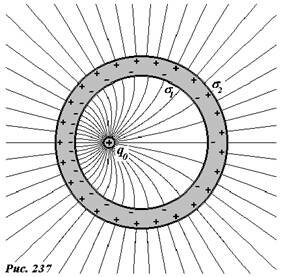
Подчеркнем, что сплошная металлическая оболочка экранирует электрическое поле, находящееся снаружи от оболочки, но не те, которые находятся внутри нее. Пусть точечный заряд +q₀ находится внутри металлической сферической оболочки (рис. 237). Этот заряд создает электрическое поле, которое индуцирует электрические заряды, как на внутренней, так и на внешней поверхностях оболочки. Рассмотрим, как в этом случае изменится распределение электрического поля.

На внутренней поверхности распределятся отрицательные заряды с некоторой поверхностной плотностью σ₁. Внутри металла напряженность поля равна нулю, поэтому отрицательные индуцированные заряды σ₁ полностью экранируют поля заряда q₀ . Используя теорему Гаусса, легко показать, что суммарный заряд, индуцированный на внутренней поверхности, равен -q₀. Суммарный заряд оболочки остается равным нулю, следовательно, на ее внешней поверхности индуцируется положительный заряд равный +q₀. На поверхностное распределение этого заряда σ₂, заряды внутренней поверхности и заряд полости не действуют, поэтому они распределятся по поверхности оболочки равномерно, и вне оболочки будут создавать электрическое поле эквивалентное полю точечного заряда +q₀, помещенного в центр сферической оболочки. Подчеркнем такое распределение поля вне оболочки не зависит от положения заряда внутри полости – смещение этого заряда приведет к изменению поля внутри полости, изменению распределения зарядов на внутренней поверхности, но не изменяет поля вне оболочки.

Чтобы «убрать» поле снаружи от оболочки ей необходимо сообщить дополнительный отрицательный заряд, такого эффекта можно добиться, заземлив оболочку.

Как распределяются заряды между двумя связанными проводящими телами?

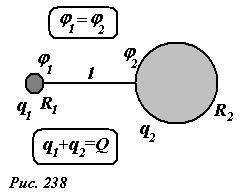
С точки зрения здравого смысла на теле больших размеров должен накапливаться больший электрический заряд. Чтобы обосновать это утверждение, рассмотрим два проводящих шара, радиусы которых обозначим R₁, R₂, находящиеся на большом расстоянии l друг от друга (l >> R₁, R₂), и соединенных проводником (рис. 238). Если этой системе сообщить электрический заряд Q, то заряды шаров q₁, q₂ распределятся так, чтобы их потенциалы были равны; суммарный же заряд системы, конечно, останется равным сообщенному заряду q₁ + q₂ = Q. Так как расстояние между шарами значительно больше их радиусов, то при расчете потенциала каждого шара можно пренебречь их взаимным влиянием и воспользоваться формулой для потенциала уединенного шара

Приравнивая эти потенциалы, получим, что заряды шаров пропорциональны их радиусам

Качественно аналогичный вывод справедлив и для проводящих тел произвольной формы. Если одно из тел значительно больше другого, то практически весь заряд окажется на большем теле. Действительно, из формул (1) следует, что при R₂ >> R₁

\(~q_1 \approx 0 ; q_2 \approx Q\) . (2)

Именно это обстоятельство используется для того, чтобы разрядить небольшое заряженное тело – его необходимо соединить с телом больших размеров. Так если к заряженному электроскопу прикоснуться рукой, то заряд перераспределится между электроскопом и телом человека, но так как размер последнего значительно больше размеров электроскопа, то можно считать, что весь заряд «сбежит» на человека. Часто в качестве тела больших размеров используют весь земной шар. Приборы, на которых не должен собираться электрический заряд «заземляют», для чего подключают их к массивному проводнику, закопанному в землю. В этом случае можно считать, что соотношения (2) выполняются точно. На схемах для указания того, что тело или прибор заземлены, используется специальное обозначение - .

Уместно привести следующую аналогию. Если небольшое тело находится в тепловом контакте с окружающей средой, то с течением времени его температура станет равной температуре окружающей среды, независимо от того, было тело первоначально нагрето или охлаждено. То есть окружающая среда может получить любое количество теплоты, или отдать любое количество теплоты, а при этом ее температура не изменяется. Такая модель окружающей среды называется термостатом. Заземление в электростатике играет такую же роль, как окружающая среда (термостат) в теории тепловых явлений.

Если рассмотренную в предыдущем разделе сферическую оболочку заземлить, то положительные заряды на внешней поверхности «исчезнут – уйдут в землю», поэтому поле вне оболочки также исчезнет (рис. 239). Можно рассуждать и в обратном порядке: если внутрь полости заземленной оболочки поместить электрический заряд, то его поле индуцирует заряды противоположного знака на внутренней поверхности, эти заряды «прибегут из заземления».

Заметим, что поле внутри заземленной полости полностью определяется ее формой и распределением зарядов внутри нее и не зависит от формы всего тела и заряда последнего.

Генератор Ван-дер-Граафа.

Как мы показали, в условиях равновесия электрический заряд распределяется по внешней поверхности проводника – это позволяет в некоторых случаях накапливать на проводниках значительные электрические заряды.

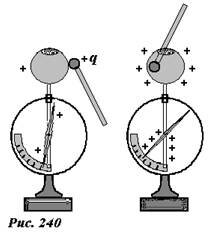
Можно провести следующий эксперимент. На изолирующей ручке расположен небольшой металлический шарик (рис. 240). Если этому шарику сообщить небольшой электрический заряд q₀ (например, с помощью стеклянной палочки) и прикоснуться шариком к поверхности сферической насадки электроскопа, то только часть этого заряда перейдет на электроскоп. Если затем опять зарядить шарик до прежнего значения заряда q₀ и опять прикоснуться к внешней поверхности насадки, то меньшая часть заряда шарика перейдет на электроскоп. Таким способом можно сообщить электроскопу только конечный заряд, сколько бы раз мы не подзаряжали шарик. Действительно, когда потенциалы уединенного шарика и электроскопа сравняются, то перераспределение зарядов прекратится. Приближенно максимальный заряд электроскопа Q_max при таком способе зарядки можно оценить из условия равенства потенциалов, поэтому \(~Q_ \approx q_0 \frac\) , где R - радиус насадки электроскопа, r - радиус шарика. Если же зарядку электроскопа проводить с помощью такого же шарика, но прикасаясь к внутренней поверхности насадки, то электроскопу можно сообщить гораздо больший заряд. Действительно, если прикоснуться шариком к внутренней поверхности, то весь его заряд перейдет на внешнюю поверхность насадки, независимо от того, какой заряд на ней находится. В этом случае максимальный заряд электроскопа будет определяться внешними причинами – при очень большом заряде насадке начнется утечка зарядов через окружающую среду, т.е. через воздух.

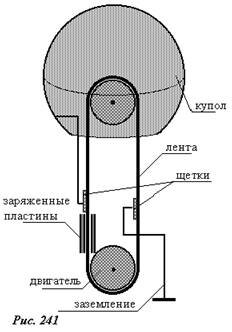
По этому принципу работают устройства, позволяющие накапливать очень большие заряды (соответственно создающие большие разности потенциалов). Одним из первых таких устройств (заметим, использующихся до настоящего времени) является электростатический генератор Ван-дер-Граафа, принципиальная схема которого показана на рисунке 241. В генераторе Ван-дер-Граафа резиновая лента приводится в движение с небольшой скоростью электродвигателем. При движении лента проходит между электрически заряженными пластинами. Возникшие на ленте индуцированные заряды снимаются с внешней поверхности ленты с помощью контактной щетки и подаются на внутреннюю поверхность металлическом купола генератора, создавая достаточно сильные электростатические поля (высокие напряжения) в окружающем купол пространстве. Заряды с внутренней стороны ленты отводятся через шину заземления. Максимальный электрический заряд купола (и его потенциал) ограничиваются только утечкой заряда с купола через воздух. Такие генераторы используются для создания высокой разности потенциалов в линейных ускорителях частиц. Диаметр купола генератора может составлять несколько метров, а создаваемая разность потенциалов несколько миллионов вольт.

Получите формулу энергии поля заряженного металлического шара

Одно из самых интересных и полезных открытий в механике — это закон сохранения энергии. Зная формулы для кинетической и потенциальной энергий механической системы, мы способны обнаруживать связь между состояниями системы в два разных момента времени, не вникая в подробности того, что происходит между этими моментами. Мы хотим определить теперь энергию электростатических систем. В электричестве сохранение энергии окажется столь же полезным для обнаружения многих любопытных фактов.

Закон, по которому меняется энергия при электростатическом взаимодействии, очень прост; на самом деле мы его уже обсуждали. Пусть имеются заряды и , разделенные промежутком . У этой системы есть какая-то энергия, потому что понадобилась какая-то работа, чтобы сблизить заряды. Мы подсчитывали работу, производимую при сближении двух зарядов с большого расстояния; она равна

Мы знаем из принципа наложения, что если зарядов много, то общая сила, действующая на любой из зарядов, равна сумме сил, действующих со стороны всех прочих зарядов. Отсюда следует, что полная энергия системы нескольких зарядов есть сумма членов, выражающих взаимодействие каждой пары зарядов по отдельности. Если и — какие-то два из зарядов, а расстояние между ними (фиг. 8.1), то энергия именно этой пары равна

Фигура 8.1. Электростатическая энергия системы частиц есть сумма электростатических энергий каждой пары

Полная электростатическая энергия есть сумма энергий всевозможных пар зарядов:

Если распределение задается плотностью заряда , то сумму в (8.3) нужно, конечно, заменить интегралом.

Мы расскажем здесь об энергии с двух точек зрения. Первая — применение понятия энергии к электростатическим задачам; вторая — разные способы оценки величины энергии. Порой легче бывает подсчитать выполненную в каком-то случае работу, чем оценить величину суммы в (8.3) или величину соответствующего интеграла. Для образца подсчитаем энергию, необходимую для того, чтобы собрать из зарядов однородно заряженный шар. Энергия здесь есть не что иное, как работа, которая затрачивается на собирание зарядов из бесконечности.

Представьте, что мы сооружаем шар, наслаивая последовательно друг на друга сферические слои бесконечно малой толщины. На каждой стадии процесса мы собираем небольшое количество электричества и размещаем его тонким слоем от до . Мы продолжаем процесс этот до тех пор, пока не доберемся до заданного радиуса (фиг. 8.2). Если — это заряд шара в тот момент, когда шар доведен до радиуса , то работа, требуемая для доставки на шар заряда , равна

Фигура 8.2. Энергию однородно заряженного шара можно рассчитать, вообразив, что его слепили, последовательно наслаивая друг на друга сферические слои.

Если плотность заряда внутри шара есть , то заряд равен

Уравнение (8.4) превращается в

Полная энергия, требуемая на то, чтобы накопить полный шар зарядов, равна интегралу по от до , т.е.

а если мы желаем выразить результат через полный заряд шара, то

Энергия пропорциональна квадрату полного заряда и обратно пропорциональна радиусу. Можно представить (8.7) и так: среднее значение по всем парам точек внутри шара равно .

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Читайте также: