Теплоемкость электронного газа в металлах
Обновлено: 04.10.2024
Перейдем теперь к рассмотрению равновесных свойств электронной подсистемы в полупроводниках и металлах. Как отмечалось, приближение самосогласованного поля позволяет задачу об электронной подсистеме свести к задаче об идеальном электронном газе.
Начнем мы с рассмотрения электронов проводимости .Как мы знаем, в отсутствие внешних полей одноэлектронный базис мы можем сформировать из блоховских состояний. Эти состояния задаются двумя квантовыми числами - квазиволновым вектором , определяющим координатную часть волновой функции, и спиновым квантовым числом , определяющим спиновую компоненту волновой функции. Поскольку в состоянии термодинамиеского равновесия с подавляющей вероятностью реализуются микросостояния, в которых подавляющая часть электронов находится вблизи дна зоны проводимости, то в наших расчетах мы можем рассматривать только такие одноэлектронные состояния. Для простоты будем рассматривать случай невырожденной зоны с изотропным параболическим законом дисперсии.
где - эффективная масса у дна зоны проводимости. Энергию мы отсчитываем от дна зоны.
Найдем плотность одночастичных стационарных состояний. По определению она есть
В рассматриваемом случае энергия одночастичного стационарного состояния вырождена по спиновому квантовому числу. Поэтому выражение под знаком суммы не зависит от спинового квантового числа , и вся сумма разбивается на две независимые суммы - по и
У электрона спиновое квантовое число может принимать только два значения . Поэтому
и таким образом,
Пользуя квазинепрерывный характер спектра квазиволнового вектора, заменяем сумму на интеграл
Подынтегральное выражение не зависит от направления волнового вектора . Поэтому интеграл разумно вычислять в сферической системе координат. Тогда интегрирование по углам дает полный телесный угол, и мы получаем
Перейдя к новой переменной интегрирования, находим
Воспользовавшись основным свойством дельта-функции Дирака, получаем
Таким образом, для среднего числа частиц и внутренней энергии имеем
Рассмотрим вначале электроны проводимости металла. В металле в качестве свободных носителей заряда выступают только электроны в зоне проводимости. Остальные электроны прочно связаны со своими ядрами и при обычных условиях не возбуждаются. Поэтому число электронов в зоне проводимости мы можем рассматривать как заданную постоянную величину, и определять химический потенциал из уравнения (11).
Начнем изучение термодинамических свойств нашего электронного газ с рассмотрения простейшего случая .
Прежде всего, установим, как в этом случае выглядит распределение Ферми-Дирака.
В случае, когда газ находится при температуре , среднее число частиц в одночастичном стационарном состоянии с волновым вектором и спиновым числом - оно же вероятность заполнения этого одночастичного стационарного состояния - имеет вид
Для того, чтобы получить распределение Ферми-Дирака при абсолютном нуле температуры, мы должны в выражении (13) перейти к пределу .
Прежде всего, определим знак химического потенциала. В принципе, возможны три варианта – химический потенциал является отрицательным, равным нулю или положительным. Давайте посмотрим, что будет происходить в каждом из этих случаев.
Пусть химический потенциал является отрицательным. Поскольку все уровни энергии , то для любого числитель аргумента экспоненты , и, соответственно, . Но тогда мы получаем, что при абсолютном нуле температуры вероятность заполнения всех одночастичных состояний равна нулю. Это явное противоречие. Таким образом, мы приходим к выводу, что химический потенциал нашего электронного газа в принципе не может быть отрицательным.
Пусть теперь химический потенциал . Тогда при отлична от нуля вероятность заполнения только двух состояний с =0. Однако принцип Паули позволяет в этих двух состояниях находиться только двум электронам, и мы вновь получаем явное противоречие.
Таким образом, мы приходим к выводу, что химический электронного газа в металле может быть только положительным.
Тогда устремив в выражении (78) , получаем следующее выражение для распределения Ферми-Дирака при абсолютном нуле температуры
Если теперь вспомнить, что согласно принципу запрета Паули в каждом одночастичном состоянии не может находиться более одного электрона, то легко видеть, что при абсолютном нуле температуры реализуются только микросостояния газа с наименьшей возможной энергией. То есть отлична от нуля только вероятность основного микросостояния. Вероятность же всех возбужденных состояний равна нулю. В основном микросостоянии электроны заполняют в соответствии с принципом Паули N низших по энергии одночпастичных стационарных состояний. Наибольшая энергия занятого одночастичного состояния в основном микросостоянии ферми-газа называется энергией Ферми. Таким образом, при абсолютном нуле температуры химический потенциал электронного газа в металле совпадает с его энергией Ферми.
Подставляя (14) в уравнение (11), получаем
Отсюда энергия Ферми
- волновой вектор Ферми, - концентрация газа.
Внутренняя энергия при Т=0
В соответствии с общим термодинамическим соотношением свободная энергия
соответственно, при абсолютном нуле
Тогда давление при Т=0
При конечной температуре становится отличной от нуля также и вероятность возбужденных микросостояний. Как легко видеть непосредственно из распределения Ферми-Дирака (78), при конечной температуре вероятность заполнения одночастичного состояния с энергией, превышающей энергию Ферми, заметно отлична от нуля только тогда, когда энергия этого состояния отстоит от энергии Ферми на величину, меньшую, либо порядка : ~ . Поэтому с подавляющей вероятностью реализуются микросостояния газа, в которых подавляющая часть электронов заселяет одночастичные состояния с энергией ~ . В этих микросостояниях доля электронов, заселяющих одночастичные состояния с энергией, большей , определяется отношением .
Поэтому для достаточно низких температур, когда с подавляющей вероятностью реализуются микросостояния, в которых подавляющая часть электронов заселяет одночастичные состояния с энергией, не превышающей энергию Ферми. Такой электронный газ называется вырожденным.
Параметр, определяющий степень вырождения, есть . Чем меньше это отношение, тем сильнее вырожден газ. Максимальное вырождение газа имеет место при абсолютном нуле температуры.
Соответственно, условие вырождения газа есть
Используя выражение (82) для энергии Ферми, условие вырождения можно записать как
Отсюда видно, что чем больше концентрация, тем в большей области температур электронный газ можно считать вырожденным. Поскольку в металлах концентрация электронов достаточно велика, то газ электронов проводимости в металлах является сильно вырожденным даже при комнатных температурах, а во многих случаях и вплоть до температуры плавления.
Таким образом, при вычислении электронной теплоемкости металла мы можем считать электронный газ вырожденным. Найдем химический потенциал и теплоемкость вырожденного электронного газа.
Тогда уравнение для химического потенциала и выражение для внутренней энергии можно записать в виде
Таким образом, наша задача свелась к вычислению интеграла
где n-целое положительное число. Поскольку мы рассматриваем вырожденный газ, то при вычислении этого интеграла нужно воспользоваться тем, что .
Выполнив обезразмеривающую замену переменной , получаем
Точкой разбиваем область интегрирования на две части
В первом интеграле делаем замену , и после несложных преобразований находим
Мы рассматриваем вырожденный электронный газ. Поэтому у нас .В знаменателе подынтегрального выражения присутствует экспонента. Поэтому подынтегральная функция быстро стремится к нулю с ростом х. Основной вклад в этот интеграл дают x этот интеграл практически не будет отличаться от своего значения с бесконечно большим пределом. Поэтому в случае вырожденного электронного газа верхний предел второго интеграла можно с большой точностью заменить на .
.Поскольку основной вклад в интеграл дают x , то функции под знаком интеграла можно разложить в ряд Тейлора в окрестности нуля. Ошибка будет очень мала. Вклад области интегрирования, в которой это разложение справедливо, очень мал. Ограничимся в разложении первым неисчезающим членом.
Соответственно, уравнение для химического потенциала принимает вид
Поскольку , то будем решать уравнение (105) методом последовательных приближений.
В нулевой приближении
В первом приближении
Ограничимся этой точностью.
Проведя разложение (107) по малому параметру с точностью до линейного члена, находим
В результате получаем зависимость хим. потенциала вырожденного электронного газа от температуры
Теплоемкость электронного газа
Проблема теплоемкости электронов проводимости на раннем этапе развития теории металлов оказалась непреодолимо трудной. Согласно классической статистической механике на каждую степень свободы частицы должна приходиться энергия, равная . На свободную частицу приходится теплоемкость, равная . В металлах ионы образуют решетку, погруженную в электронный газ свободных электронов, концентрация которых примерно такая же, как и число атомов. Поэтому теплоемкость металлов должна складываться из теплоемкости решетки и теплоемкости электронного газа :
Если бы электронный газ был обычным классическим (невырожденным) газом, то каждый электрон обладал бы энергией , а энергия электронного газа, заключенного в одном моле металла, была бы равна ; его теплоемкость - . Таким образом общая теплоемкость металла в области больших температур должна быть равна, согласно (2.26), .
В действительности металлы и диэлектрики в области высоких температур, в которой выполняется закон Дюлонга и Пти, установленный еще в 1819 г., обладают теплоемкостью ~ . Получается так, что электронный газ практически не вносит заметного вклада в общую теплоемкость. Этот результат совершенно непонятный с классической точки зрения нашел свое объяснение в квантовой теории.
Действительно, обратившись к функции плотности состояний , можно качественно объяснить теплоемкость электронного газа (рис. ).
Когда мы нагреваем образец от абсолютного нуля, не каждый электрон в нем приобретает энергию ~ , как следовало бы из классической теории газов. Испытывают тепловое возбуждение и приобретают энергию ~ лишь электроны, находящиеся в состояниях с энергией в интервале вблизи уровня Ферми.
Если - полное число электронов, то тепловое возбуждение при повышении температуры от 0 до может испытать только часть электронов порядка отношения , потому что приблизительно такая их доля обладает энергиями в энергетическом интервале в верхней части энергетического распределения.
Каждый из электронов обладает избыточной тепловой энергией порядка , а полная энергия теплового возбуждения электронов составляет величину порядка
Электронную теплоемкость получим, взяв производную по температуре от полной энергии теплового возбуждения
Таким образом электронная теплоемкость ~ ; при комнатной температуре много меньше значения , которое дает классическая теория, примерно в 100 раз.
Получим более точное выражение для электронной теплоемкости, справедливое для области низких температур, удовлетворяющее условию . Полное изменение энергии системы электронов (рис. ) представим в виде двух частей:
Здесь - функция Ферми-Дирака, - число состояний на единичный энергетический интервал. Число частиц умножим на , в результате получим:
Теперь продифференцируем (2.28) и (2.29) по :
Вычтем (2.31) из (2.30); тогда для электронной теплоемкости получим:
При низких температурах ( , для которых и ведется рассмотрение, производная велика только при энергиях близких к , и поэтому вместо функции можно взять ее значение при и вынести ее из под знака интеграла; в результате получим:
В приближении первого порядка по температуре в выражении для функции распределения Ферми - Дирака химический потенциал можно заменить постоянной величиной . Тогда
вводя обозначение можно переписать (2.33)
Так как в подинтегральном выражении пренебрежимо мало, то можно нижний предел в интеграле заменить на - . Получающийся определенный интеграл – табличный:
Теперь для получим:
Для свободного электронного газа , отсюда для получим:
Этот результат находится в согласии с качественным результатом (2.27). Таким образом, сравнивая и , получим
где - число молей. Так электронный газ в металлах является вырожденным, термическому возбуждению даже в области высоких температур подвергается лишь незначительная доля свободных электронов (~ 1%); остальные электроны энергию не поглощают. Иначе обстоит дело в области низких температур, близких к абсолютному нулю. В этой области теплоемкость решетки с понижением температуры падает ~ и вблизи абсолютного нуля может оказаться столь малой, что основное значение может приобрести , которая с понижением температуры падает значительно медленнее ( ~ ). На рис. приведена температурная зависимость теплоемкости сплава (20%V+80% Сr).
8.3. Теплоёмкость электронного газа в металлах
В металлах теплоёмкость складывается из теплоёмкости ионной решётки (см. параграф 8.2.) и теплоёмкости свободных электронов - электронного газа., т. е. С = Cреш + Сэл . Если бы электронный газ был невырожденный (классический), то каждый электрон обладал бы средней кинетической энергией (3/2)kT и средняя энергия электронного газа в одном моле металла была бы равна (3/2)kTNA = (3/2)RT. Полная внутренняя энергия моля металла в этом случае была бы U = 3RT + (3/2)RT = (9/2)RT, а молярная теплоёмкость металла С = dU/dT = (9/2)R, т. е. в полтора раза больше теплоёмкости диэлектриков. Однако в действительности теплоёмкость металлов не отличается существенно от теплоёмкости неметаллических кристаллов.
Это противоречие устраняется квантовой теорией.
Средняя энергия теплового движения, равная kT, составляет при комнатной температуре 1/40 эВ. Такая энергия может возбудить только малую часть электронов, находящихся на самых верхних энергетических уровнях, примыкающих к уровню Ферми. Энергия Ферми EF для хорошо проводящих металлов составляет 6 эВ [см. (7.4) и комментарий этой формулы]. Действительно, расчёт показывает, что молярная теплоёмкость электронного газа

,
что примерно в 150 раз меньше теплоёмкости твёрдого тела С = 3R при Т = 300 К.
Относительный вклад теплоёмкости электронного газа в теплоёмкость металла будет увеличиваться с уменьшением Т, когда теплоёмкость С, пропорциональная Сэл , которая пропорциональна Т.
Таким образом, квантовая теория объяснила и теплоёмкость металлов.
Лекции 9,10. Электрические свойства кристаллов
9.1. Классическая электронная теория электропроводности металлов
Опыты, проведенные Рикке в 1901 г., Мандельштамом и Папалекси в 1913 г., Толменом и Стюартом в 1916 г. показали, что носителями тока в металлах являются электроны. Ток в металлах можно вызвать крайне малой разностью потенциалов. Это даёт основание считать, что электроны перемещаются по металлу практически свободно. Появление этих свободных электронов объясняется тем, что при образовании кристаллической решётки от атомов металлов легко отрываются слабее всего связанные валентные электроны. Можно показать, что концентрация их достигает электронов в . При такой высокой концентрации электронов средняя сила, действующая на электрон со стороны всех остальных электронов и ионов, равна нулю и, следовательно, электроны можно считать свободными частицами и их взаимодействие с ионами можно рассматривать как ряд последовательных соударений.
В этом приближении система электронов может анализироваться как система одноатомных молекул идеального газа. Исходя из этого, Друде и позднее Лоренц распространили результаты кинетической теории газов (см лекции 1,2) на свободные электроны - на так называемый электронный газ и получили законы Ома, Джоуля-Ленца в дифференциальной форме.
В позапрошлом семестре изучались эти законы [см. конспект лекций, ч. II, формулы (16), (38) в лекциях 6,7].
Плотность тока проводимости равна произведению удельной электрической проводимости проводника на напряжённость электрического поля в проводнике, т.е.

- закон Ома в дифференциальной форме. (1)
Удельная тепловая мощность тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряжённости электрического поля в проводнике, т. е.

- закон Джоуля-Ленца в дифференциальной форме, (2)
где в (1) и (2) - удельная электропроводность ( = 1/).
Друде и Лоренц показали, что для металлических проводников

, (3)
где n - концентрация свободных электронов, e и m - заряд и масса электрона, -средняя длина свободного пробега электрона, v - средняя скорость теплового движения электрона. Согласно формуле (30) в лекции 1,2 v и при Т = 300 К, (масса электрона ), .
Скорость же направленного движения (скорость дрейфа электрона), возникающего благодаря электрическому полю . Для , (заряд электрона ), vдр = = 0,78 мм/с, т. е. много меньше скорости теплового движения электрона.
Итак, классическая теория объяснила законы Ома, Джоуля-Ленца, Видемана-Франца. Вместе с тем она имеет ряд недостатков.
Строгий анализ с использованием квантовой теории показал, что не все валентные электроны свободно движутся по решётке с тепловыми скоростями, а лишь малая их часть. Подавляющее число валентных электронов в электропроводимости (как и в теплоёмкости) не участвуют. Это приводит к расхождениям между классической теорией и практикой. Например, из (3) следует, что , а на практике в большом диапазоне изменения температур 1/Т.


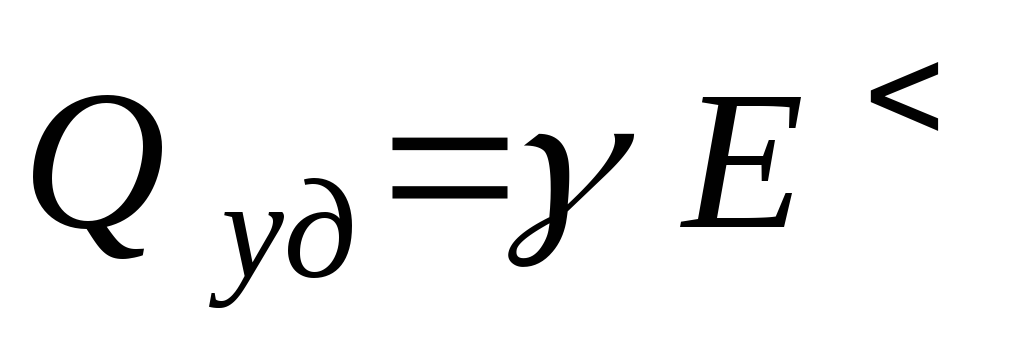

Относительный вклад теплоёмкости электронного газа в теплоёмкость металла будет увеличиваться с уменьшением Т, когда теплоёмкость С, пропорциональная [см. (9)], уменьшается и она будет сравнима или даже будет меньше Сэл , которая пропорциональна Т.
- закон Ома в дифференциальной форме. (1)
Читайте также:
- Из чего состоит металлическая дверь в квартиру
- Почему простое вещество свинец проявляет металлические свойства
- Веществом при диссоциации которого в качестве катионов образуются только ионы металла
- Под барабан стиральной машины попал металлический предмет как вытащить
- Термическая обработка закалка металлов
