Зависимость сопротивления металлов и сплавов от температуры
Обновлено: 26.07.2024
К основным свойствам проводниковых материалов относятся:
- Удельная проводимость или обратная ей величина – удельное сопротивление;
- Температурный коэффициент удельного сопротивления;
- Удельная теплопроводность;
- Контактная разность потенциалов и термоэлектродвижущая сила;
- Предел прочности при растяжении и относительное удлинение при разрыве.
Удельное сопротивление проводников. Величину, обратную удельной проводимости g называют удельным сопротивлением r и для проводника с постоянным поперечным сечением определяют по формуле:
Единицей удельного сопротивления в СИ является Ом×м, однако в практике чаще пользуются внесистемной единицей мкОм×м.
Следует отметить, что в отличие от диэлектриков диапазон удельных сопротивлений металлических проводников достаточно мал – от 0,016мкОм×м. для серебра и примерно до 10 мкОм×м. для железо-хромо-кобальто-алюминиевых сплавов, т.е. занимает всего три порядка.
Температурная зависимость удельного сопротивления металлических проводников. Как было показано ранее в идеально чистых металлах единственной причиной, которая ограничивает длину свободного пробега, являются тепловые колебания узлов кристаллической решетки (фононы). Удельное сопротивление металла, обусловленное этим фактором, обозначим как ρТ.. С ростом температуры возрастают амплитуды фононов и связанные с этим флюктуации периодического поля решетки. Это повышает рассеивание электронов, уменьшает длину свободного пробега и вызывает возрастание удельного сопротивления. Для упрощенной одномерной модели решетки длина свободного пробега электронов определяется как:
где λсв - длина свободного пробега;
Δa - амплитуда фононов;
N - концентрация атомов в металле.
Потенциальная энергия атома, отклоненного на Δa от узла решетки:
где Купр - коэффициент упругости связи.
Согласно классической статистике средняя энергия одномерного гармоничного осциллятора равняется КТ. Тогда:
½ · Kупр (Δa) 2 = КТ (4.6)
где К - постоянная Больцмана.
Тогда из (4.5), (4.6) получим:
Если подставить (4.7) в (4.2) получим:
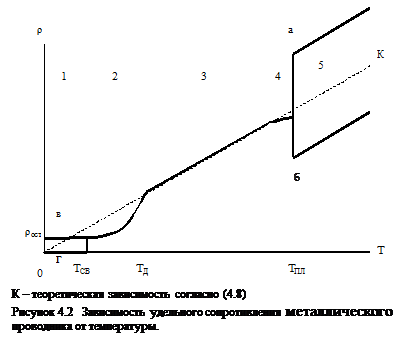
То есть с ростом температуры удельное сопротивление чистых металлов должно возрастать линейно. В действительности эта зависимость является более сложной (рисунок 4.2)
На участке 3 при комнатных температурах зависимость ρ = ¦(Т) линейна, как это видно из (4.8). То есть с ростом температуры возрастает амплитуда тепловых колебаний узлов кристаллической решетки, что уменьшает длину свободного пробега электронов.
На участке 4 вблизи температуры плавления имеет некоторая нелинейность, что объясняется другими механизмами рассеивания электронов.
При переходе металла из твердого состояния в жидкое (температура плавления Тпл) может иметь место как резкое возрастание удельного сопротивления (а), так и его уменьшение (б). Это связано с изменением структуры кристаллической решетки. Если при плавлении объем металла возрастает, что имеет место для большинства металлов, то расстояние между атомами тоже возрастает, металлическая связь уменьшается, а амплитуда фононов возрастает, что уменьшает длину свободного пробега электронов, следовательно, сопротивление металла возрастает. Для некоторых металлов (висмут, галлий) при плавлении объем металла уменьшается, что усиливает связи между атомами, амплитуда фононов уменьшается и удельное сопротивление тоже уменьшается.
На участке 5 металлы находятся в жидком состоянии и сохраняют кристаллическую решетку, поэтому зависимость удельного сопротивления от температуры поясняется аналогично участку 3.
На участке 2, ниже температуры Дебая (ТД) изменяется частота тепловых колебаний узлов кристаллической решетки, поэтому зависимость ρ = ¦(Т) нелинейна и подчиняется закону:
ρ = A·T n (4.9)
где n - изменяется от 1 до 5.
На участке 1 некоторые металлы имеют конечное сопротивление (rост) даже при температуре Т=0 К. Это объясняется наличием в металле статических дефектов решетки, прежде всего примесей. Это позволяет оценивать чистоту металлов на основании отношения:
где ρ300K , ρ4K - соответственно удельное сопротивление металла при 300 К и 4,2 К (температура кипения жидкого гелия). Чем меньше это отношение, тем чище металл.
У некоторых металлов при температуре ниже Тсв наблюдается резкое уменьшение удельного сопротивления до нуля. Такое явление называют сверхпроводимостью.
Таким образом, согласно (4.9) металлические проводники в обычных условиях имеют линейную зависимость удельного сопротивления от температуры.
Влияние примесей на удельное сопротивление металлических проводников.Как уже говорилось, причинами рассеяния электронов в металлах являются не только тепловые колебания узлов кристаллической решетки, но и наличие статических дефектов, которые, прежде всего связанные с примесями. Рассеивание на статических дефектах не зависит от температуры. Поэтому при абсолютном нуле сопротивление реальных металлов остается конечным. Из этого следует правило Маттиссена об аддитивности удельного сопротивления:
где ρпр - полное сопротивление металла с примесью;
ρт - сопротивление, обусловленное рассеянием электронов на фононах;
ρост - остаточное сопротивление, обусловленное рассеиванием электронов на статических дефектах решетки.
Наибольший вклад в остаточное сопротивление вносит рассеяние на примесных атомах, которые практически всегда имеются в металлах. Поэтому длина свободного пробега электронов в металлах с примесью состоит из:
где lТ, lД - длина свободного пробега электронов, ограниченная фононами и примесями, соответственно.
Длина пробега lД:
где Nd - концентрация атомов примеси;
Sd – эффективная плоскость рассеивания электронов атомами примеси.
Тогда удельное сопротивление проводника с примесью:
То есть наличие примесь увеличивает удельное сопротивление металла, но его зависимости от температуры остается линейной (рис. 4.3)
Dρост = а +b(DZ) 2 (4.14)
где Dρост - изменение остаточного сопротивления при изменении примеси;
DZ - разность валентностей собственного атома и атома примеси;
а, b - константы.
Таким образом, на сопротивление металлов меньшее влияние оказывают примесные атомы металла, а большее – атомы металлоидов.
В технике очень широко используют металлические сплавы, имеющие значительную концентрацию атомов примеси, со структурой неупорядоченного твердого раствора. Статическое распределение атомов разного вида в узлах кристаллической решетки вызывает значительные флюктуации периодического поля кристалла, рассеивающего электроны. Но в неупорядоченных твердых растворах, преимущественно с добавкой примеси, изменяется только период решетки. Поэтому действителен закон Нордгейма:
де С - константа;
xА, xВ - атомные доли компонентов в сплаве.
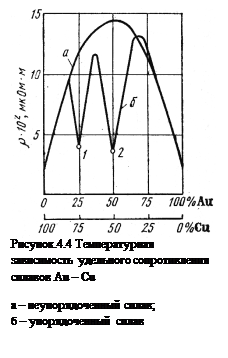
То есть в бинарных твердых растворах А-В остаточное сопротивление возрастает, как при добавлении атомов металла В к металлу А, так и при добавленные атомов металла А к металлу В (рис. 4.4). Остаточное сопротивление достигает максимума при xА = xВ = 0,5.
Закон Нордгейма описывает изменение остаточного сопротивления для непрерывных неупорядоченных твердых растворов. Если сплав отжечь, то он может стать упорядоченным и, если при этом возникают интерметаллические соединения, которые имеют собственную кристаллическую решетку, то зависимость остаточного сопротивления разделяется на части, соответственно числу интерметаллических соединений. Таким образом, удельное сопротивление металлических сплавов всегда выше сопротивления чистых металлов. Это свойство используется для получения высокоомных проводниковых материалов.
Изменение удельного сопротивления при упругих деформациях объясняется изменением амплитуды колебания узлов кристаллической решетки металла. Увеличение амплитуды колебания узлов решетки металла приводит к уменьшению длины свободного пробега носителей заряда и удельное сопротивление возрастает. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может вновь снижено до первоначальных значений.
Температурный коэффициент удельного сопротивления.В диапазоне температуры, где зависимость r от t близка к линейной (рис. 4.2, участок 3) допустима линейно-кусочная аппроксимация этой зависимости, и величина удельного сопротивления в конце диапазона температуры t может быть подсчитана по формуле
где r0—удельное сопротивление в начале диапазона.
Величину ar из выражения (4.) называют средним температурным коэффициентом удельного сопротивления в данном диапазоне температуры:
Дифференциальное выражение для ar имеет вид
Значения ar чистых металлов в твердом состоянии близки друг к другу, и поэтому приближенно можно считать ar » 0,004 , К -1 .
Исключение составляют элементы, относящиеся к ферромагнетикам — железо, никель, кобальт, гадолиний, а также натрий, калий, хром и др., однако и для них ar отличается от приведенной величины только в 1,5—2 раза.
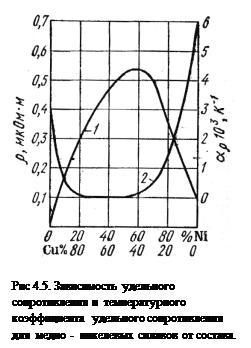
Наличие примесей уменьшает значение αρ. У некоторых сплавов αρ. даже может приобретать небольшие отрицательные значения (рис.4.5). Это объясняют тем, что при более сложных составе и структурax по сравнению с чистыми металлами сплавы нельзя рассматривать как классические металлы, т. е. изменение проводимости их обусловливается не только изменением подвижности носителей заряда но в некоторых случаях и частичным возрастанием концентрации носителей при повышении температуры. Сплав, у которого уменьшение подвижности с увеличением температуры компенсируется возрастанием концентрации носителей заряда, имеет нулевой температурный коэффициент удельного сопротивления.
Это явление используется для изготовления термостабильных сплавов, например, константана, манганина ). Константан - сплав с 60% Ni и 40% Сu имеет большое сопротивление (~0,5 мкОм×м) и очень малый температурный коэффициент (меньше 10 -6 К -1 ), отсюда и его название.
Удельная теплопроводность металлов. Высокая теплопроводность металлов легко объясняется посредством передачи тепловой энергии атомов нагретого участка металла атомам холодного участка за счет переноса этой энергии коллективизированными электронами. Так как механизм электропроводности и теплопроводности в металлах обусловлен одними и теми же факторами: движением электронного газа и его плотностью, очевидно, что металлы с высокой электропроводностью являются также хорошими проводниками тепла, а диэлектрики обладают не только низкой электропроводностью, но и низкой теплопроводностью. Так, медь имеет удельную теплопроводность 406 Вт/К×м, серебро 453 Вт/К×м, алюминий 218 Вт/К×м, что значительно выше чем у диэлектриков. Удельная теплопроводность и электропроводность металлов связаны законом Видемана-Франца:
где lТ - удельная теплопроводность.
σ - удельная электропроводность.
L0 - число Лоренца.
Поскольку на участке комнатных температур удельная электропроводность падает пропорционально температуре, то согласно (4.19), удельная теплопроводность металлов не должна зависеть от температуры. Это следствие из закона Видемана-Франца выполняется для большинства металлов. Это свойство применяют в технике, при использовании металлов как радиаторов для охлаждения мощных полупроводниковых приборов.
Для этой цели необходимо использовать металлы с большим значением удельной теплопроводности. Чаще всего, это сплавы на основе алюминия (силумин), которые имеют хорошие тепловые, механические и антикоррозийные свойства. Медь нельзя использовать вследствие её плохой коррозионной стойкости, а серебро - вследствие высокой стоимости.
Контактные явления и термоэлектродвижущая сила (термо-э.д.с.)
При соприкосновении двух разных металлов, между ними возникает контактная разность потенциалов. Согласно квантовой теории причиной этого является различная энергия Ферми соприкасающихся металлов. Пусть в изолированном состоянии электронный газ в металлах А и В имеет энергию Ферми WF A и WF B , отсчитываемую от дна зоны проводимости (рис.4.6).
Термодинамическая работа выхода электронов из металла равняется, соответственно, cА и cВ. Поскольку кинетическая энергия электронов, которые находятся на уровне Ферми в разных металлах различна, то при контакте материалов возникает значительный переход электронов из металла В с большим значением энергии Ферми в металл, где эта энергия меньше. Например, из металла В в металл А. Вследствие этого металл В заряжается положительно, а металл А - отрицательно. Между ними возникает разность потенциалов, которая блокирует дальнейший переход носителей заряда. Равновесие наступит, если:
где UK - контактная разность потенциалов.
контактная разность потенциалов достигает несколько вольт.
Термоэлемент, который построен из двух различных металлических проводников с замкнутой цепью, называют термопарой (рис.4.7).
Вольтметр в такой цепи будет показывать разность потенциалов, которую называют термоэлектродвижущей силой (термо-э.д.с.). Термо-э.д.с. равняется:
где aT — относительная удельная термо-э.д.с.
Значение aT зависит от природы материалов и температуры и включает в себя три составляющих. Первая обусловлена температурной зависимостью контактной разности потенциалов, поскольку с ростом температуры уровень Ферми в металлах незначительно, но смещается.
Вторая составляющая обусловлена диффузией носителей заряда от горячих спаев к холодным. Поскольку существует градиент температуры от контакта к контакту, то возникает диффузия электронов от горячего контакта к холодному, что дает некоторый вклад в возникающую разность потенциалов.
Третья составляющая возникает вследствие захвата электронов квантами тепловой энергии. Их поток тоже передвигается к холодному контакту. Значение aT приблизительно равняется нескольким мкВ/К.
Термопары часто используют для измерения температуры. Если температуру холодного контакта поддерживать 0 О С, то вольтметр будет показывать напряжение пропорциональное температуре горячего контакта. Достоинством термопар является высокая линейность, возможность измерения температуры в широком интервале температур, независимость значения термо-э.д.с. от длины проводников.
Вследствие того, что значение aT зависит от состава материала и незначительно от температуры, термопары градуируют, используя точки плавления металлов: свинца, олова, серебра и других.
Наиболее распространенными термопарами являются:
· Хромель- копель (типа ХК). Она позволяет измерять температуры до 600 О С и имеет при этой температуре термо-э.д.с. приблизительно 50 мВ.
· Хромель-алюмель (типа ХА). Она используется к температурам 1000 О С и имеет при этой температуре термо-э.д.с. приблизительно 40 мВ.
· Медь-константан. Ее используют при низких температурах до 350 О С. При этой температуре термо-э.д.с. достигает 15 мВ.
· Платинородий-платина (типа ПП или ППР). Ее применяют до температуры 71600 О С. Термо-э.д.с. у этой термопары невелика (приблизительно 14 мВ при 1600 О С). Но она позволяет обеспечить наиболее точные и стабильные измерения температуры.
Однако явление термо-э.д.с. имеет и отрицательные стороны. В реальных условиях исключить градиенты температур практически невозможно. Поэтому, если контактируют различные металлы, то возможно возникновение паразитной термо-э.д.с. Для устранения этого в цепях (прежде всего электроизмерительных устройств), надо подбирать контактирующие металлы с малыми значениями термо-э.д.с. Такой парой, например, является медь-манганин.
Зависимость электрического сопротивления от температуры
При проектировании электрических схем, инженеры сталкиваются с тем, что проводники обладают определенным сопротивлением, на которое оказывают влияния температурные колебания. Статья даст подробное описание, что такое зависимость сопротивления от температуры и как температура влияет на проводимость различных веществ — металлов, газов и жидкостей. Дополнительно будет приведена формула расчета такой зависимости.

Сопротивление
Сопротивлением называется способность проводника пропускать через себя электрический ток. Единицей измерения данной физической величины является Ом. На принципиальных схемах эта величина обозначается буквой «R». На величину сопротивления любого проводника электрическому току влияет его структура. Двигаясь внутри структуры, свободные электроны сталкиваются с атомами и электронами, которые замедляют их движение. Чем их концентрация больше, тем выше будет само электрическое сопротивление.

О способности проводников проводит электрический ток судят по величине его удельного сопротивления. Удельное сопротивление проводника — это сопротивление протеканию тока через проводник из любого вещества с площадью поперечного сечения 1 м² и длиной один метр. Обозначается в физике данная величина буквой «ρ». Данный параметр является табличной величиной и измеряется в системе СИ как Ом×м (может также измеряться в Ом×см и Ом×мм²/м).

Коэффициент сопротивления
Во время работы электрических цепей прослеживается прямая зависимость сопротивления металлов от температуры. Это явление называют коэффициентом температурного сопротивления. Оно определяет соотношение сопротивления к температурным изменениям. Объясняется это явление следующим образом: с повышением температуры структура проводника получает долю тепловой энергии, вследствие чего эта энергия увеличивает скорость движения атомов. В результате повышается вероятность их столкновения со свободными электронами. Чем чаще происходят эти столкновения, тем ниже будет проводимость.
Можно провести простой опыт: в электрическую схему из аккумулятора и омметра подключим кусок медной проволоки. При таком подключении схема будет иметь строго определенное значение сопротивления. Далее надо будет нагреть медную проволоку. В момент нагрева можно заметить, что сопротивление всей схемы растет, а после остывания проводника оно наоборот уменьшается. На основании такого опыта довольно просто прослеживается температурная зависимость сопротивления проводника.

Температурный коэффициент отображает увеличение сопротивления при изменении температуры вещества на 1 градус. Для максимально чистого металла это значение равняется 0.004 °С -1 . То есть, при увеличении температуры на 10 градусов, электрическая проводимость в металлах изменится на 4 % в большую сторону. Данная величина обозначается буквой «α». При расчете сопротивления через удельное сопротивление используется такая формула:

В данной зависимости:
- «R» — сопротивление, Ом;
- «l» — длина проводника, м;
- «s» — поперечное сечение проводника, м²;
- «ρ» — значение удельного сопротивления, Ом×м.
Зависимость проводимости металлического проводника от температуры можно проследить с помощью таких выражений:

Для металлов все предельно просто — изменение температуры приводит к увеличению его сопротивления. Ниже будет дано описание этой зависимости для газов, которые по своей природе являются диэлектриками.
Для закрепления материала, решим следующую задачу:
Имеется стальной проводник, диаметр которого равен один миллиметр, а длина его составляет 100 метров. Определите сопротивление такого проводника из стали, если величина удельного сопротивления стального проводника составляет 12×10 -8 Ом×м.
Определяем сопротивление проводника по формуле:
где S является площадью поперечного сечения. Определить площадь можно с помощью формулы:
S= π×r 2 = π×d 2 /2 2 =3.14×(1×10 -3 ) 2 /4=3.14×10 -6 /4=0.785×10 -6 м 2
После этого можно определить сопротивление:
R=12×10 -8 ×100/(0.785×10 -6 )=15.287 Ом
Газы не являются проводниками, но их проводимость так же зависит от температуры. Происходит это за счет так называемого эффекта ионизации. Ионизация в газах происходит за счет насыщения их жидкостью или иными веществами, которые способны проводить электрический ток. Проследить то, как увеличивается сопротивление при повышении температуры газа можно на таком опыте.

К схеме с амперметром и аккумулятором добавим 2 металлические пластины, которые не соприкасаются друг с другом. Такая электрическая цепь является разомкнутой. Между пластинами поместим зажженную горелку. При нагреве происходит смещение стрелки амперметра в сторону увеличения. То есть такую цепь можно считать замкнутой. На основании этого можно сделать вывод, что с ростом температуры воздух ионизируется, происходит снижение его сопротивления и увеличение проводимости заряженных электронов. Данный эффект называют пробоем изоляционного слоя газа, зависящий от степени их ионизации и величины протекающего напряжения. Подобное явление знакомо каждому из нас — это грозовой разряд.
Жидкости
В жидкостях прослеживается обратная зависимость. С увеличением температуры, сопротивление жидкого проводника уменьшается. Для электролита свойственно правило отрицательного значения температурного коэффициента — а˂0. Удельное сопротивление электролита рассчитывается следующим образом:
При этом увеличившееся значение температуры электролита сопровождается уменьшением сопротивления и ростом его проводимости.
Сверхпроводимость
Снижение температуры металлических проводников сильно увеличивает их проводимость. Это связано с тем, что в структуре вещества замедляется движение атомов и электронов, благодаря чему снижается вероятность их столкновения со свободными электронами. При температуре абсолютного 0 (–273 градуса Цельсия) возникает явление падения до нуля сопротивления проводника. Зависимость сопротивления проводника от температуры при абсолютном 0 — сверхпроводимость.
Температура, при которой обычный проводник становится сверхпроводником, называется критической. Она будет разной для различных чистых металлов и сплавов. Все будет зависеть от их структуры, химического состава и структуры кристаллов. Например, серое олово с алмазной структурой является полупроводником. Но белое олово при своей тетрагональной кристаллической ячейке, мягкости и плавкости, переходит в состояние сверхпроводника при температуре 3.70 К. Также при критической температуре прослеживается целый ряд других способностей:
- Повышение частоты переменного тока вызывает рост сопротивления, значение гармоник с периодом световой волны.
- Способность удерживать величину силы тока ранее приложенного, а затем отключенного источника.

Металл или сплав может перейти в состояние сверхпроводника и при нагревании. Такое явление называют высокотемпературной проводимостью. Ответ на вопрос, почему от высокой температуры сопротивление металлов снижается, может довольно просто объяснить их кристаллическая структура. В момент нагрева до критических значений, электроны перестают хаотично перемещаться внутри структуры вещества. Они выстраиваются в цепочку. Такое построение не мешает движению свободных электронов, а значит падает общее сопротивление. Переход в состояние высокотемпературной проводимости начинается с порога 1000К и этот показатель выше, чем точка кипения азота.
Применение
Свойство проводников изменять сопротивление при определённой температуре используют для создания различных элементов электрических схем и измерительных приборов. О них будет рассказано далее в данной статье.
Резистор
Сопротивление устройств старого типа сильно зависело от их нагрева. При нагревании проводимость резистора пропорционально изменялась в меньшую сторону. Для электрических цепей требуется идеальный резистор, который обладает наивысшим коэффициентом проводимости. Для снижения нагрева при производстве данных устройств теперь используется материал, имеющий малую зависимость сопротивления от температуры нагрева. Это позволило применять резисторы с малым сопротивлением для цепей с большим напряжением.

Терморезистор
Существует отдельная группа резисторов, которые применяют для измерения температуры. Особенностью такого устройства является то, что он может снижать свою проводимость при нагреве. При этом он отключает цепь при достижении определенного порогового значения.

Термометр сопротивления
Это прибор был разработан для измерения температуры среды. Он состоит из тонкой платиновой проволоки, защитного чехла и корпуса. Прибор имеет стабильную реакцию на перепады температуры. Измеряемой величиной в данном устройстве служит сопротивление этой проволоки из платины. Чем выше будет температура, тем сопротивление соответственно будет больше. Понижение сопротивления так же фиксируется, так как в этот момент меняются проводимость и сопротивление. Для измерения температуры термометром сопротивления, в настоящее время применяются проволочные индикаторы из разнообразных металлов. В зависимости от свойств используемого металла, погрешность устройства может составлять не более 0.1 %. Благодаря этому достигается очень высокая точность измерения температуры.

Самый известный нам газовый проводник — это люминесцентная лампа. Газ нагревается за счет увеличения напряжения между анодом и катодом лампы.

Известным жидкостным проводником является щелочной аккумулятор. При понижении температуры нарушается структура жидкости и изменяется ее сопротивление.

Нагрев провоцирует движение атомов и электронов, увеличивая сопротивление и зарядный ток устройства.
Заключение
В данной статье мы рассмотрели, как зависит сопротивление от температуры. Металлы, газы и жидкости имеют свойства изменять свою проводимость и сопротивление при температурных перепадах. Это свойство изменения электрического сопротивления используются для измерения температуры среды. Наибольшая точность измерений температуры в настоящее время достигается за счет применения современных материалов, даже в бытовой технике.
Физика. 10 класс
§ 34. Электрический ток в металлах. Сверхпроводимость
Типичными представителями класса проводников являются металлы. Какова природа электрического тока в металлах?
Природа электрического тока в металлах. В металлических проводниках носители электрического заряда — свободные электроны. Под действием внешнего электрического поля свободные электроны упорядоченно движутся, создавая электрический ток ( рис. 194 ).
Электронная проводимость металлов была впервые экспериментально подтверждена немецким физиком К. Рикке ( 1845–1915 ) в 1901 г. Суть опыта Рикке заключалась в следующем: по проводнику, состоявшему из трёх отполированных и плотно прижатых друг к другу цилиндров — двух медных и одного алюминиевого ( рис. 195 ), в течение года проходил ток одного и того же направления. За этот промежуток времени через проводник прошёл заряд более 3,5 МКл. После завершения опыта взвешивание показало, что массы цилиндров остались неизменными. Это явилось экспериментальным доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются одинаковыми для всех металлов, т. е. электронами.
В 1916 г. американский физик Р. Толмен ( 1881—1948 ) и шотландский физик Т. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением свободных электронов.
В этих опытах катушку с большим числом витков тонкой проволоки подключали к гальванометру и приводили в быстрое вращение вокруг своей оси ( рис. 195.1 ). При резком торможении катушки в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда. По направлению отклонения стрелки гальванометра было установлено, что электрический ток создают отрицательно заряженные частицы. При этом экспериментально полученное отношение заряда каждой из этих частиц к её массе (удельный заряд) близко к удельному заряду электрона, полученному из других опытов. Так было экспериментально доказано, что носителями свободных зарядов в металлах являются электроны.
Вещества, обладающие электронной проводимостью, называют проводниками первого рода.
В соответствии с классической электронной теорией проводимости металлов, созданной немецким физиком П. Друде ( 1863–1906 ) в 1900 г., металлический проводник можно рассматривать как физическую систему, состоящую из свободных электронов и положительно заряженных ионов, колеблющихся около положений равновесия ( рис. 196 ).
Появление свободных электронов при образовании металлического кристалла из нейтральных атомов можно упрощённо объяснить следующим образом. Электроны, находящиеся на внешних оболочках атомов, слабо связаны со своими ядрами. При образовании кристалла атомы сближаются на расстояние r 0,1 нм , и электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов. В результате этого их взаимодействие с собственными ядрами значительно ослабевает, вследствие чего они теряют с ними связь и могут двигаться по всему кристаллу в любом направлении как свободные частицы. Атомы превращаются при этом в положительно заряженные ионы. В пространстве между ионами беспорядочно движутся подобно частицам идеального газа свободные электроны. Поэтому для описания движения электронов используют модель «электронный газ» — совокупность свободных электронов в кристаллической решётке металла. На рисунке 196.1 пунктирной линией изображена траектория движения одного из электронов.
В этой модели электроны, упорядоченное движение которых является током проводимости, рассматривают как материальные точки, модуль потенциальной энергии взаимодействия которых пренебрежимо мал по сравнению с их кинетической энергией. Считают, что движение электронов под действием электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими, т. е. при столкновениях электроны полностью передают ионам кинетическую энергию своего упорядоченного движения. В промежутках между столкновениями свободные электроны совершают беспорядочное тепловое движение и в то же время движутся упорядоченно и равноускоренно под воздействием электрического поля.
Интересно знать
Модель электронного газа позволяет теоретически объяснить природу сопротивления и обосновать закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов. Проанализируем упорядоченное движение электронов проводимости.
Пусть электрон движется с ускорением в направлении, противоположном направлению напряжённости электрического поля ( рис. 196.2 ): где m0 — масса электрона, e — элементарный электрический заряд (модуль заряда электрона).
Тогда модуль средней скорости его направленного движения: , где — усреднённый промежуток времени между двумя последовательными столкновениями электрона с ионами кристаллической решётки.
Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля где l — длина проводника, U — напряжение между его концами. Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника .
Сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:
где q — модуль заряда электронов проводимости, находящихся в проводнике, — усреднённое время прохождения этих электронов по проводнику, N — количество электронов проводимости в проводнике, n — концентрация этих электронов, V = Sl — объём проводника. Следовательно, сила тока пропорциональна напряжению между концами проводника I U.
Конспект по теме "Зависимость сопротивления от температуры"
ВСПОМНИМ: Величина, характеризующая противодействие электрическому току в проводнике, которое обусловлено внутренним строением проводника и хаотическим движением его частиц, называется электрическим сопротивлением проводника.
Аналогично тому, как трение в механике препятствует движению, сопротивление проводника создает противодействие направленному движению зарядов и определяет превращение электрической энергии во внутреннюю энергию проводника. Причина сопротивления: столкновение свободно движущихся зарядов с ионами кристаллической решетки.
В СИ единицей электрического сопротивления проводников служит ом [Ом]. Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Электрическое сопротивление проводника зависит от размеров и формы проводника и от материала, из которого изготовлен проводник.
S – площадь поперечного сечения проводника
l – длина проводника
ρ – удельное сопротивление проводника.
Сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения.
Величину ρ, характеризующую зависимость сопротивления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением проводника. Оно численно равно сопротивлению проводника длиной 1 м и площадью сечения 1 мм 2 , изготовленного из данного вещества. Единица удельного сопротивления в СИ [1 Ом*м = 1 Ом*мм 2 /м]
Сопротивление проводника зависит и от его состояния, а именно от температуры.
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решетки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1 0 температуры, называется температурным коэффициентом сопротивления и обозначается буквой α (альфа). Если при температуре t0 сопротивление проводника равно R0, а при температуре t равно R, то температурный коэффициент сопротивления:
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200° С).
Из формулы для температурного коэффициента сопротивления определим R^
R= α + = ( α +1)
Зная, как зависит сопротивление металлического проводника от температуры, можно, измерив сопротивление проводника, определить его температуру. Этот факт положен в основу работы так называемых термометров сопротивления. Датчик размещают в среде, температуру которой надо измерить. Сопротивление провода измеряется специальным прибором, и по известному сопротивлению определяют температуру среды. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи. Шкалу данного прибора градуируют в единицах температур.
При нагревании размеры проводника меняются мало, а в основном меняется удельное сопротивление.
Удельное сопротивление проводника зависит от температуры:

где ρ0 - удельное сопротивление при 0 градусов,
t - температура,
α - температурный коэффициент сопротивления
( т.е. относительное изменение удельного сопротивления проводника при нагревании его на один градус)
Для металлов и сплавов
Обычно для чистых металлов принимается
Таким образом, для металлических проводников с ростом температуры
увеличивается удельное сопротивление, увеличивается сопротивление проводника и уменьшается электрический ток в цепи.
Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока более чем в 10 раз.
У некоторых сплавов, например, у сплава меди с никелем (константан), температурный коэффициент сопротивления очень мал: α ≈ 10 -5 K -1 . Удельное сопротивление константана велико: ρ ≈ 10 -6 Ом∙м. Такие сплавы используют для изготовления эталонных сопротивлений и добавочных сопротивлений к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Вывод. Удельное сопротивление (соответственно и сопротивление) металлов растет линейно с увеличением температуры.

Сверхпроводимость металлов и сплавов . У многих металлов и сплавов при температурах, близких с T=0 К, наблюдается резкое уменьшение удельного сопротивления – это явление называется сверхпроводимостью металлов. Оно было обнаружено голландским физиком Х.Камерлингом – Онессом в 1911 году у ртути (Ткр=4,2К). Разработали квантовую теорию сверхпроводимости Д.Бардин, л.Купер, Д.Шриффер и Н.Н.Боголюбов
Реакция на примеси . Введение примеси в сверхпроводник уменьшает резкость перехода в сверхпроводящее состояние. В нормальных металлах ток исчезает примерно через 10-12 с. В сверхпроводнике ток, может циркулировать годами (теоретически 105 лет!).
Применение сверхпроводимости . 1.Сооружаются мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле без затрат электроэнергии на длительном интервале времени, т.к. выделения теплоты не происходит. 2.Сверхпроводящие магниты используются в ускорителях элементарных частиц, магнитогидродинамических генераторах, преобразующих энергию струи раскаленного ионизированного газа, движущегося в магнитном поле, в электрическую энергию. 3.Высокотемпературная сверхпроводимость в недалеком будущем приведет к технической революции в радиоэлектронике, радиотехнике. 4. Если удастся создать сверхпроводники при комнатной температуре, то генераторы и электродвигатели станут исключительно компактны и передавать электроэнергию будет возможно на большие расстояния без потерь.
1. Определить сопротивление железной проволоки, нагретой до 200°С, если сопротивление ее при 0° было 100 Ом. Температурный коэффициент железа 0,0066:
2. Определить сопротивление медного провода двухпроводной линии передачи при + 20°С и +40 °С, если сечение провода S =
= 120 мм , а длина линии l = 10 км.
По справочным таблицам находим удельное сопротивление меди при + 20 °С и температурный коэффициент сопротивления :
3. = 0,0175 Ом • мм /м; = 0,004 град .
+Определим сопротивление провода при Т1 = +20 °С по формуле R = , учитывая длину прямого и обратного проводов линии:
Зависимость сопротивление от температуры

Зависимость электрического сопротивления от температуры.
Температурный коэффициент характеризует зависимость электрических свойств вещества проводника от температуры.
Единицей измерения температурного(термического) коэффициента сопротивления в СИ является К-1.


В 1911 году нидерландский физик Х. Камерлинг-Оннес обнаружил интересное явление. Ученый охлаждал различные металлы и измерял их сопротивление.Выяснилось что при некоторой критической температуре сопротивление скачком падало почти до 0. Для ртути он получил критическую температуру равную 4,12 К (-269). Это явление сверхпроводимости.
Сверхпроводимостью называется явление резкого уменьшения сопротивления чистых металлов и ряда сплавов почти до нулевого значения при температурах, близких к абсолютному нулю. Материалы, обнаруживающие это явление, называются сверхпроводниками.
Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбуждённый в сверхпроводящем кольце ток может идти неограниченно долго без изменения.

Задача 1. Сопротивление медного провода при 0°С равно 4 Ом. Найдите его сопротивление при 50 °С, если температурный коэффициент сопротивления меди α = 4,3 • 10-3К-1

Задача 2. Сопротивление проводника при 20 °С равно 25 Ом, а при 35 °С — 25,17 Ом Найдите температурный коэффициент сопротивления.

Выбранный для просмотра документ Зависимость сопротивления от температуры.docx
Тема: Зависимость электрического сопротивления от температуры. Сверхпроводимость
Цели урока:
Образовательные: сформировать понятия: температурный коэффициент сопротивления, сверхпроводимость; создать условия для формирования у обучающихся представления об электрическом сопротивлении, научить решать задачи на применение формулы зависимости сопротивления проводника от температуры;
Воспитательные: Воспитание мотивов учения, положительного отношения к знаниям; воспитание эстетических взглядов в процессе учебной деятельности учащихся, в том числе самостоятельно применять знания в повседневной жизни.
Развивающие: учить делать заключения по аналогии о закономерностях различных физических явлений; формировать умения применять общий закон (закон Ома) для участка цепи в частных ситуациях.
1. Организационный момент(1-2мин)
2. Фронтальный опрос. (5 мин)
- Сформулируйте закон Ома для участка цепи.
- Что называют сопротивлением?
- Что принято за единицу сопротивления?
- От чего и как зависит сопротивление проводника?
- Что называется удельным сопротивлением проводника?
- Каковы единицы удельного сопротивления проводника?
- Что называют сила тока?
- Что называют электрическим напряжением?
3. Самостоятельная работа по домашнему заданию(10мин)
Привести в соответствие строки в 1 и 2 графе
1) Электрическое сопротивление проводника
А) сопротивление проводника из данного вещества длиной 1м, площадью поперечного сечения 1м 2
2) Какие вещества имеют большое уд.сопротивление
Б) Удельное сопротивление проводника рассчитывается по формуле
3)
В) прибор для измерения сопротивления
4) Единица измерения сопротивления
Г) прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника
5)
Д)
6) Единица измерения удельного сопротивления
Е) Сопротивление проводника рассчитывается по формуле
Ж) фарфор, эбонит
8) Причина электрического сопротивления
З)
9) Удельным сопротивлением проводника называется
И) столкновения электронов и ионов
10)
К) Сопротивление проводника рассчитывается по формуле через закон Ома
1 – Г, 2 – Ж, 3 – Е, 4 – З, 5 – Б, 6 – Д, 7 – В, 8 – И, 9 – А, 10 – К.
4. Изучение нового материала. Видео. (20 мин)
Тема сегодняшнего урока «Зависимость электрического сопротивления от температуры. Сверхпроводимость»
Открываем учебники записываем тему урока.
Сопротивление проводника R зависит от его размеров и материала. Также сопротивление проводника зависит от его температуры. Давайте посмотрим видео с опытом со спиралеобразной проволокой.
Как вы заметили, что ток в цепи уменьшается по мере нагревания спирали. Сделаем вывод: сопротивление железной проволоки при нагревании увеличивается.
У всех металлов сопротивление при нагревании увеличивается, другое дело чистый это металл или сплав. Имеются специальные сплавы, сопротивление которых почти не меняется при повышении температуры. К таким сплавам относятся константан и манганин.
Почему же возрастает сопротивление при нагревании как вы думаете?
Дело в том, что при повышении температуры проводника усиливаются колебания ионов в узлах кристаллической решетки. В результате этого электроны чаще сталкиваются с ионами и это мешает протеканию тока.
Зависимость электрического сопротивления от температуры.


Температурный коэффициент характеризует зависимость электрических свойств вещества проводника от температуры.
Единицей измерения температурного(термического) коэффициента сопротивления в СИ является К -1 .
Графически это можно представить так:


Зависимость сопротивления проводника от температуры используется в устройстве термометров сопротивления. Один из точных термометров является платиновый.
В 1911 году нидерландский физик Х. Камерлинг-Оннес обнаружил интересное явление. Ученый охлаждал различные металлы и измерял их сопротивление.Выяснилось что при некоторой критической температуре сопротивление скачком падало почти до 0. Для ртути он получил критическую температуру равную 4,12 К (-269Сверхпроводимостью называется явление резкого уменьшения сопротивления чистых металлов и ряда сплавов почти до нулевого значения при температурах, близких к абсолютному нулю. Материалы, обнаруживающие это явление, называются сверхпроводниками.
Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбуждённый в сверхпроводящем кольце ток может идти неограниченно долго без изменения.
Читайте также:
