Определить удлинение стержня ав стальной стержень длиной 3м нагружен силой 240 кн
Обновлено: 18.05.2024
Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна то после нагружения она станет равной (рис. 1.6). Величину называют абсолютным удлинением стержня.
Будем считать, что абсолютное удлинение и деформации связаны только с напряжениями, возникающими в стержне. В действительности имеются и другие факторы, влияющие на деформации. Так, деформации зависят от температуры и времени действия нагрузки. Неупругие деформации зависят от “истории” нагружения, т.е. от порядка возрастания и убывания внешних сил. Пока, однако, этих вопросов мы касаться не будем.
Если стержень нагружен только силой Р, то напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях; деформация по оси стержня остается одной и той же, равной своему среднему значению по длине
Эта величина называется относительным удлинением стержня.
Если стержень нагружен сосредоточенной силой Р и распределенными силами (наиболее общий случай), то относительное удлинение не будет постоянным по длине стержня. Получим выражение для относительного удлинения стержня, рассматривая элемент стержня между плоскостями и
до и после нагружения (см. рис. 1.6). Если обозначить перемещение плоскости АА элемента стержня через и, то плоскость будет иметь перемещение, равное и где - дополнительное перемещение из-за растяжения элемента стержня. Тогда относительное удлинение элемента будет равно
Заметим, что вследствие равномерного распределения напряжений по сечению удлинения для всех элементарных отрезков (см. рис. 1.6), взятых на участке оказываются одинаковыми. Следовательно, если концы отрезков до нагружения образуют плоскость, то и после нагружения стержня они образуют плоскость, но смещенную вдоль оси стержня. Это положение может быть взято в основу толкования механизма растяжения и сжатия и трактуется как гипотеза плоских сечений (гипотеза Бернулли). Если эту гипотезу принять как основную, то тогда из нее, уже как следствие, вытекает высказанное ранее предположение о равномерности распределения напряжений в поперечном сечении.
В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода. Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и а, т.е. в мегапаскалях. Вместе с тем, поскольку модуль упругости может иметь довольно большие числовые значения, его предпочтительнее измерять не в мега-, а в гигапаскалях:
Для наиболее часто применяемых материалов модуль упругости Е имеет следующие значения,
Закон Гука представляет собой простейшую и очевидную аппроксимацию наблюдаемой в опытах зависимости удлинения от напряжения. Естественно, что точность этой аппроксимации определяется в первую очередь тем, сколь широкий диапазон изменения напряжения имеется в виду. Всегда можно подобрать достаточно малый интервал напряжений, чтобы в его пределах функцию можно было бы с заданной точностью рассматривать как линейную. И конечно, для разных материалов это выглядит по-разному. Для некоторых материалов, таких как, например, сталь, закон Гука соблюдается с высокой степенью точности в широких пределах изменения напряжений. Для отожженной меди, для чугуна этот интервал изменения напряжений существенно меньше. В тех случаях, когда закон Гука явно не соблюдается, деформацию задают в виде некоторой нелинейной функции от напряжения с таким расчетом, чтобы эта функция отвечала кривой, полученной при испытании материала.
Вернемся к выражению (1.4) и заменим в нем а на на Тогда получим
В результате получаем систему, состоящую из двух уравнений: первого уравнения системы (полагая ) и уравнения (1.5), которая позволяет определить напряженно-деформированное состояние прямолинейного стержня, нагруженного осевыми силами:
Из первого уравнения системы (1.6) находим осевое усилие а из второго - Получаемые выражения для и и будут содержать две произвольные постоянные, определяемые из двух краевых условий: при
Абсолютное удлинение стержня переменного сечения на длине будет равно
В том случае, когда стержень нагружен только по концам, нормальная сила не зависит от Если, кроме того, стержень имеет постоянные размеры поперечного сечения то из выражения (1.5) получаем
При решении многих практических задач возникает необходимость наряду с удлинениями, обусловленными напряжением учитывать также удлинения, связанные с температурным воздействием. В этом случае пользуются способом
наложения и деформацию с рассматривают как сумму силовой и чисто температурной деформации:
где а - коэффициент температурного расширения материала.
Для однородного стержня, нагруженного по концам и равномерно нагретого, получаем
Таким образом, силовая и температурная деформации рассматриваются как независимые. Основанием этому служит экспериментально установленный факт, что модуль упругости Е при умеренном нагреве слабо меняется с температурой, точно так же как и а практически не зависит от . Для стали это имеет место до температуры порядка . При более высоких температурах необходимо учитывать зависимость Е от
Рассмотрим примеры определения напряжений и перемещений в некоторых простейших случаях растяжения и сжатия.
Пример 1.1. Требуется выявить закон изменения нормальных сил, напряжений и перемещений по длине ступенчатого стержня, нагруженного на конце силой Р (рис. 1.7, а), определить числовые значения наибольшего напряжения и наибольшего перемещения, если Материал - сталь, Поскольку сила Р велкка, собственный вес стержня можно не учитывать.
Из условий равновесия любой отсеченной части стержня вытекает, что нормальная сила в каждом сечении стержня равна внешней силе Р. Построим график изменения силы вдоль оси стержня. Графики подобного рода называются в сопротивлении материалов эпюрами. Они дают наглядное представление о законах изменения различных исследуемых величин. В данном случае эпюра нормальной силы представлена на рис. 1.7, б прямоугольником, поскольку На рисунке эпюра заштрихована линиями, которые проведены параллельно откладываемым на графике значениям . В данном случае значение силы откладывают вверх, поэтому штриховка проведена вертикально.
Для того чтобы получить эпюру напряжений а, надо ординаты эпюры изменить обратно пропорционально величине (рис. 1.7, в). Большее значение а равно
Определим перемещение и каждого сечения стержня по направлению силы Р. Перемещение сечения равно удлинению отрезка длиной . Следовательно, согласно формуле (1.6), . Таким образом, на участке изменения от нуля до I перемещение и пропорционально z (рис. 1.7, а). На втором участке стержня перемещение Зависимость и от также будет линейной. Наибольшее перемещение имеет торцевое сечение стержня: мм.
Пример 1.2. Построить эпюры нормальных сил, напряжений и перемещений для свободно подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 1.8, о). Длина стержня площадь поперечного сечения плотность материала у.
Нормальная сила в сечении z равна весу нижележащей части стержня: Следовательно, нормальная сила пропорциональна г. Эпюру в данном случае штрихуют горизонтальными линиями, поскольку
значения откладывают в горизонтальном налравденхн (рис. 1.8, в). Наг пряжение в сечении равно (см. рис. 1.8, в).
Перемещение и в сечении z равно удлинению верхнего участка стержня. Согласно формуле (1.5),
Таким образом, закон изменения и изображается квадратичной функцией 2. Наибольшее перемещение «шах имеет нижнее торцевое сечение (рис. 1.8, г):
Пример 1.3. Колонна (рис. 1.9, а) нагружена силой Р и силами собственного веса. Требуется подобрать такой закон изменения площади поперечного сечения чтобы напряжения во всех сечениях были одинаковы и равны Построить эпюры нормальных сил, напряжений и перемещений.
На расстоянии от торца нормальная сжимающая сила равна
По условию задачи
Дифференцируя обе части этого равенства по z, получим или После интегрирования находим
При следовательно, и тогда искомый закон изменения площади принимает вид
Построение эпюр удобнее всего начинать с эпюры напряжения которое вдоль оси колонны по условию не меняется (рис. 1.9, б). Поскольку напряжение постоянно, то постоянным будет и относительное удлинение е. Поэтому перемещение и возрастает пропорционально расстоянию от основания колонны (рис 1.9, в).
Нормальная сила в сечении z равна Эпюра показана на рис. 1.9, г.
Рассмотренная задача относится к числу часто встречающихся в сопротивлении материалов задач на отыскание условий равнопрочности. Если напряжение в некотором теле (в данном случае в колонне) будет постоянно для всех точек объема, такую конструкцию называют равнопрочной. В подобных конструкциях материал используется наиболее эффективно.
Пример 1.4. Кронштейн нагружен на конце силой Р (рис. 1.10, а). Требуете подобрать поперечное сечение стержней АВ и с таким расчетом, чтобы возникающие в них напряжения имели одинаковую заданную величину а. При этом угол а должен быть выбран из условия минимального веса конструкции при заданном вылете кронштейна
Из условий равновесия узла В (рис. 1.10, б) находим нормальные силы в стержнях: .
Далее определяем площади поперечного сечения стержней по величине заданного напряжения и:
Вес конструкции кронштейна пропорционален объему: Подставляя длины и площади стержней, находим
Задача 8 – Расчет сжатых стержней на устойчивость
Задание. Стальной стержень длиной l сжимается силой F. Требуется:
1) найти размеры поперечного сечения при допускаемом напряжении на сжатие [σ] = 160 МПа (расчет производить последовательными приближениями, предварительно задавшись коэффициентом φ = 0,5);
2) найти значение критической силы и коэффициент запаса устойчивости.
Данные взять из таблицы 8.
Таблица 6 –Исходные данные к задаче 8
Пример 8. Рассмотрим стальной стержень, представленный на рисунке 31.

Рисунок 31 – Расчетная схема стержня
Данные для расчета F = 400 кН; м.
Площадь стержня определим, исходя из условия устойчивости
где – коэффициент уменьшения основного допускаемого напряжения для сжатых стержней.
Расчет приведем последовательными приближениями.
а) Определим площадь поперечного сечения стержня:
б) Выразим площадь поперечного сечения заданной формы через размер d (рисунок 31а):
Отсюда определим размер d:
в) Выразим минимальный радиус инерции через размер сечения d:
где Jmin – минимальный момент инерции поперечного сечения
стержня относительно одной из главных центральных
г) Найдем гибкость стержня:
где коэффициент, учитывающий характер закрепления
концов стержня (коэффициент приведенной длины).
По найденной гибкости стержня определим табличное значение коэффициента [2, 3]:
д) Определим расчетное напряжение в стержне при и :
Недонапряжение стержня составит
Недогрузка стержня велика, поэтому необходимо сделать перерасчет.
2. Выполним второе приближение, приняв
а) Снова определим площадь поперечного сечения стержня:
б) Найдем размер d:
в) Рассчитаем радиус инерции:
г) Определим гибкость:
д) Проверим расчетное напряжение в стержне:
3. Сделаем третье приближение, приняв .
а) Определим площадь:
б) Тогда, размер равен:
в) Следовательно, радиус инерции
г) Затем найдем гибкость стержня:
Табличное значение коэффициента определим в этом случае методом интерполирования.
д) Проверим расчетное напряжение
Недонапряжение стержня равно
Отклонение напряжения от номинальной величины допускается в инженерных расчетах в пределах 4 – 5 %. Следовательно, третье приближение является окончательным. Необходимый размер сечения Площадь поперечного сечения .
4. Определим величину критической силы.
Поскольку гибкость данного стержня по нашим расчетам меньше предельной гибкости для стали Ст. 3 ( , то для определения критического напряжения следует использовать формулу Ясинского:
где а и в – эмпирические коэффициенты, зависящие от свойств
Следовательно, критическая сила
Найдем коэффициент запаса устойчивости


Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
© cyberpedia.su 2017-2020 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
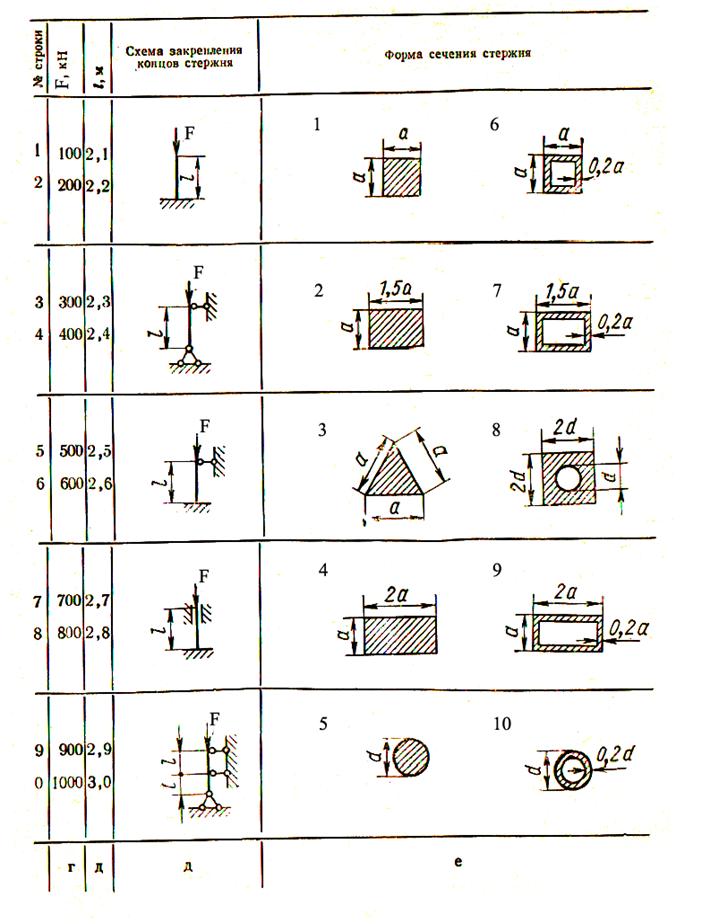
Диаграмма растяжения низкоуглеродистой стали
Особые точки диаграммы растяжения обозначены точками 1,2,3,4,5.
1) Точка 1 соответствует пределу пропорциональности: удлинение
2) Точка 2 соответствует пределу упругости материала, материал теряет упругие свойства – способность вернуться к исходным размерам.
3) Точка 3 является концом участка, на котором образец сильно деформируется без увеличения нагрузки. Это явление называется текучестью.
4) Точка 4 соответствует максимальной нагрузке, в этот момент на образце образуется шейка – резкое уменьшение площади поперечного сечения.
Расчетная формула при растяжении и сжатии
В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы или разрушение деталей конструкции.
Предельным напряжением называютПредельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких - предел прочности. Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных.
Отношение предельного напряжения к напряжению, возникающему в процессе работы делали, называют коэффициентом запаса прочности и обозначают буквой S: .
Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Сечение, для которого коэффициент запаса прочности наименьший, называется опасным.
Минимально необходимый коэффициент запаса прочности называют допускаемым и обозначают [S]. Отношение предельною напряжения к допускаемому коэффициенту запаса прочности называют допускаемым напряжением и обозначают [
Условие прочности детали конструкции заключается в том, что наибольшее возникающее в ней напряжение (рабочее) не должно превышать допускаемого: Расчетная формула при растяжении и сжатии имеет види читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле , не должно превышать допускаемое.
При расчете конструкций па прочность встречаются три вида задач, различающихся формой использования расчетной формулы:
1. проектный расчет, при котором определяются размеры опасного сечения по формуле 2. проверочный расчет, при котором определяется рабочее напряжение и сравнивается с допускаемым по формуле . Проверочный расчет выполняем по формуле:Если брус не догружен на 15 % и перегружен на 5 %, то условие прочности выполняется.
3. определение допускаемой нагрузки ведется по формулеПрактическое задание:
Вариант 1
1. Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса
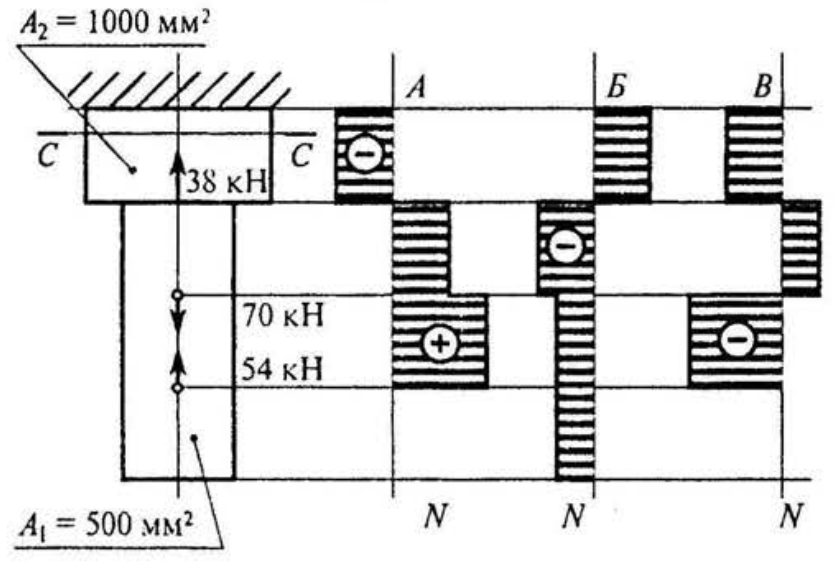
2. Для бруса из вопроса 1 определить наибольшую продольную силу, возникшую в поперечном сечении.
3. Определить нормальное напряжение в сечении С - С бруса из вопроса 1.
4. Чему равен коэффициент запаса прочности в сечении С - С бруса, если механические характеристики материала: σT =220 МПа; σB =400 МПа. Использовать результаты, полученные при ответе на вопрос 3.
5. Определить удлинение стержня АВ. Стальной стержень длиной 3 м нагружен силой 240 кН; форма поперечного сечения стержня -швеллер № 10; модуль упругости материала 2·10 5 МПа.
Вариант 2
1. Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса.
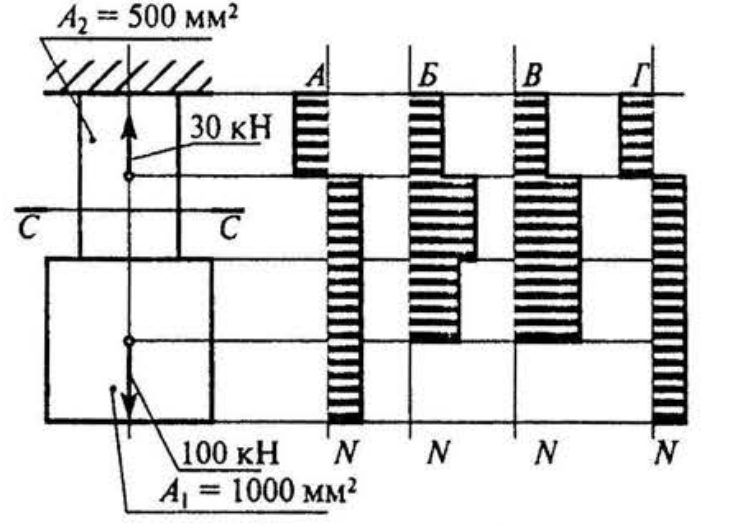
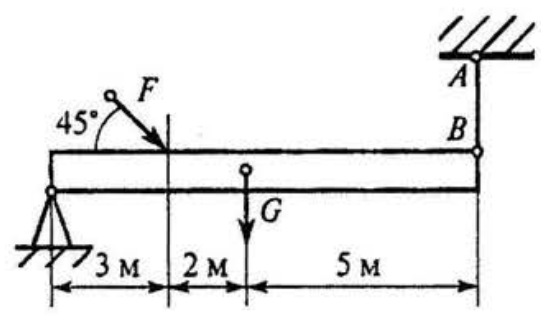
4. Обеспечена ли прочность бруса в сечении С - С бруса (вопрос 3), если известны механические характеристики материала: σT = 560 МПа; σB = 870 МПа; а допускаемый коэффициент запаса прочности [s] = 2.
5. Однородная жесткая плита весом G =20 кН нагружена силой F = 10 кН. Длина стержня АВ =4 м; материал - сталь Е = 2·10 5 МПа; форма поперечного сечения - двутавр №10. Определить удлинение стержня АВ.
Вариант 3
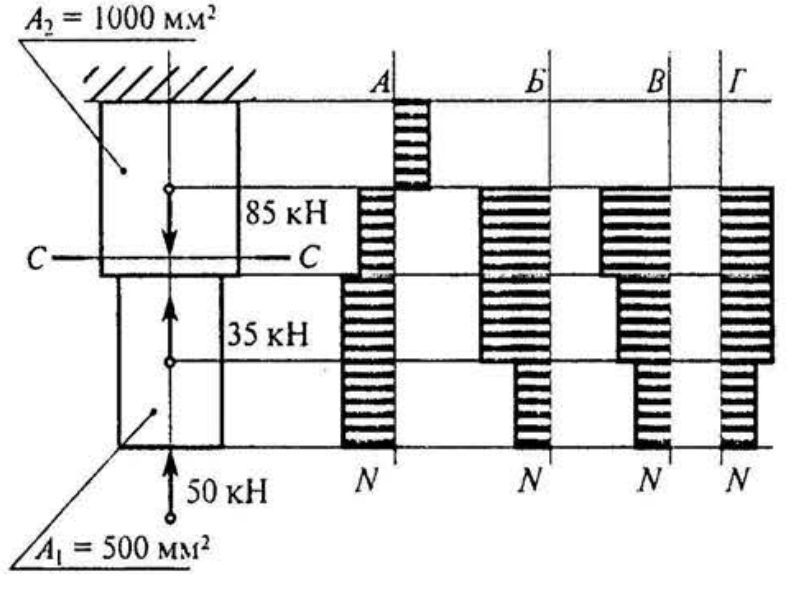
4. Чему равен коэффициент запаса прочности в сечении С - С бруса, если механические характеристики материала: σT =280 МПа; σB =560 МПа. Использовать результаты, полученные при ответе на вопрос 3.
5. Стальной стержень длиной 4 м нагружен силой 360 кН; форма поперечного сечения стержня - швеллер № 8; модуль упругости материала Е= 2·10 5 МПа. Определить удлинение стержня АВ.
Вариант 4
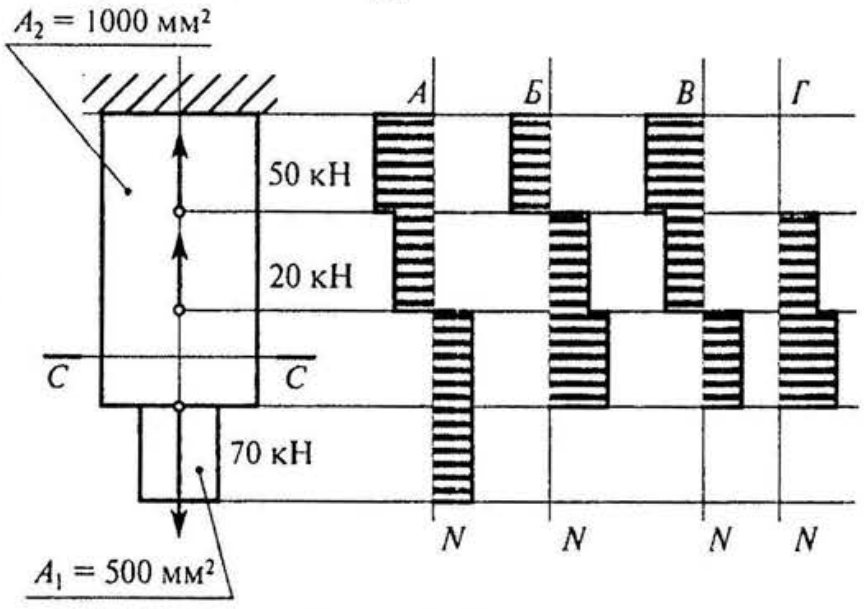
3. Определить нормальное напряжение в сечении С - С 100 МПа бруса из вопроса 1.
4. Обеспечена ли прочность бруса в сечении С-С (вопрос 3), если известны механические характеристики материала: σT =280 МПа; σB =560 МПа.; допускаемый коэффициент запаса прочности [s] =4. Схема бруса представлена на рисунке к вопросу 1.
5. Однородная жесткая плита весом G = 4 кН нагружена силой F =2 кН. Длина стержня АВ =6 м; материал- сталь Е= 2·10 5 МПа; форма поперечного сечения - швеллер № 6,5. Определить удлинение стержня АВ

ПРАКТИЧЕСКАЯ РАБОТА № 11
по дисциплине техническая механика
Тема: Построение эпюр сжатия и растяжения.
Цель занятия: Научится строить эпюры продольных сил и нормальных напряжений
Место проведения: учебная аудитория
Форма организации занятия: Практическое занятие
Литература для самоподготовки:Олофинская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий
Теоретические сведения:

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Определение усилий в стержнях скрепленных шарнирно
Пример решения задачи по определению усилий в двух стержнях, скрепленных шарнирно между собой и с вертикальной опорной стеной, в точке соединения которых подвешен груз.
Задача
Груз Q=1000Н удерживается с помощью двух невесомых стержней, шарнирно скрепленных между собой в точке A и в шарнирах B и C с вертикальной стеной (α=60°, β=30°).
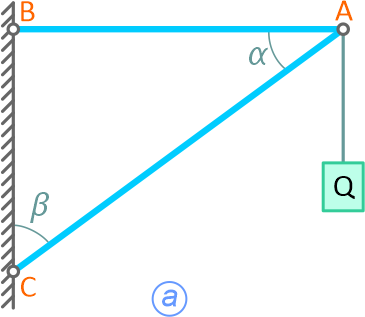
Определить усилия в стержнях AB и BC (рисунок 2.1,а).
Решение
Короткое видео про реакции в разных типах связей:
В данном случае следует рассмотреть равновесие точки A, т.к. все силы приложены в этой точке.
Нить с грузом натянута силой Q. В равновесии точку A удерживают два невесомых стержня. Их реакции всегда направлены вдоль стержней.
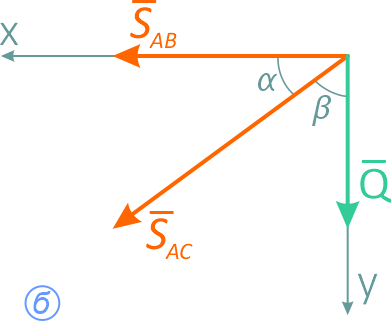
Реакции принято направлять от узла (точки A), т.е. предполагается, что стержни работают на растяжение (рисунок 2.1, б). В случае отрицательного ответа при решении уравнений стержень работает на сжатие.
При равновесии системы сил выполняется равенство
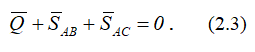
Это векторное равенство можно построить. Откладываем в масштабе известную силу Q, к концу вектора прибавляем SAB, т.к. его величина и направление неизвестны, проводим через конец вектора Q горизонтальную линию (параллельно SAB, рисунок 2.1, б).
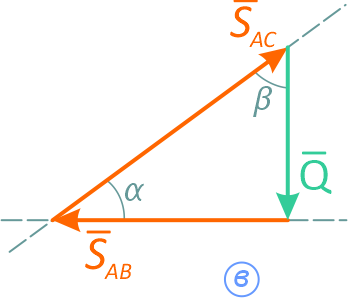
Замыкающий вектор SAC должен пройти через начало вектора Q под углом β к вертикали. Результатом построения является замкнутый треугольник (рисунок 2.1, в). Величины усилий в стержнях можно получить, умножая замеренные значения векторов сил на масштаб или воспользовавшись теоремой синусов:
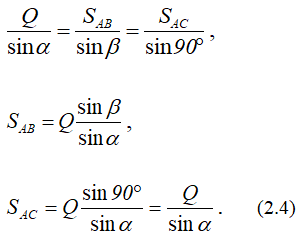
Направление силы SAC в силовом треугольнике говорит о том, что этот стержень работает на сжатие.
Задача может быть решена и аналитически. Для этого выбираем систему координат xAy (рисунок 2.1, б) и проецируем на ее оси векторное равенство (2.3):
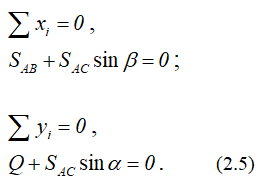
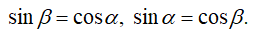
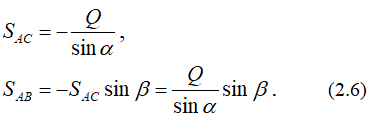
То есть и в этом решении по знакам в ответах получаем, что стержень AC работает на сжатие, а стержень AB – на растяжение.


Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Читайте также:
