От чего зависит коэффициент продольного изгиба при расчете центрально сжатого стального стержня

Обновлено: 01.05.2024

Условием устойчивости сжатого стержня является неравенство:

Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:

1) от длины стержня, от размеров и даже от формы поперечных сечений,

2) от способа закрепления концов стержня,

3) от материала стержня.

Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.

Поэтому

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности: В этом случае

гдеσт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатиеσвс).

С учетом сказанного условие устойчивости сжатого стержня принимает вид:

Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня

μ – коэффициент приведенной длины (зависит от способов закрепления концов стержня), ℓ - геометрическая длина стержня,

i– радиус инерции поперечного сечения

Коэффициентφ изменяется в диапазоне0≤φ≤1, зависит ,как уже говорилось, как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆λ=10.

При вычислении значений φ для стержней, имеющих значения гибкости не кратные числу 10, применяется правило линейной интерполяции.

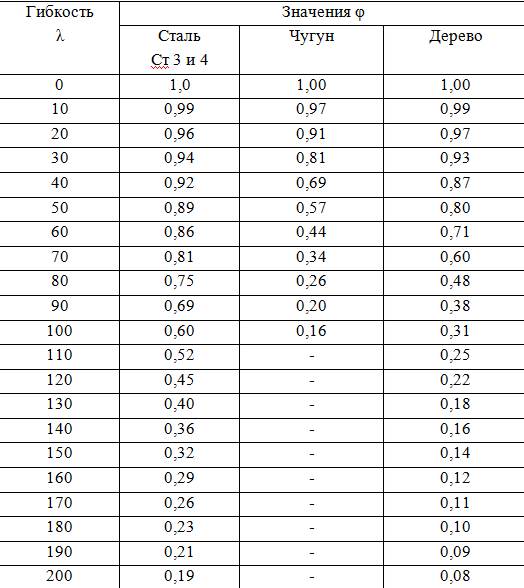
Значения коэффициента φ в зависимости от гибкости λ для материалов

На основании условия устойчивости решаются три вида задач:

Проверка устойчивости.
Подбор сечения.
Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ[σ]А.

Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:

Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции , от которой зависит значение коэффициента продольного изгибаφ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:

1 попытка: задаемся φ1 из средней зоны таблицы, находим , затем гибкость и сравниваем со значением φ1 . Если

2 попытка: принимаем , определяем размеры сечения, вычисляем , по таблице определяем , то:

3 попытка: принимаем , определяем размеры сечения, вычисляем , по таблице определяем

Процесс приближений продолжается до тех пор, пока разница не окажется менее 5%.

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Устойчивость сжатых стержней

Продольный изгиб

При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.

Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение.

Рассмотрим известные виды равновесия.

Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы, стремящиеся удалить её от начального положения.

Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.

При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.

При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.

Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.

Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.

Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.

Критическая сила. Критическое напряжение

Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.

При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаны Эйлером.

В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:

Критическое напряжение вычисляется следующим образом

, где гибкость стержня ,

а радиус инерции сечения.

Введем понятие предельной гибкости.

Величина λ_пред зависит только от вида материала:

Если у стали 3 Е=2∙10 11 Па, а σ_пц=200МПа, то предельная гибкость

Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80

Таким образом, для стержней большой гибкости λ≥λ_пред критическая сила определяется по формуле Эйлера.

В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ₀≤λ≤λ_пр, (стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.

где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа, b=1,14МПа.

При значениях гибкости стержня 0≤λ≤λ₀ (стержни малой гибкости) потеря устойчивости не наблюдается.

Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.

Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:

В этом случае ,

где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).

Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня , где:

i – радиус инерции поперечного сечения относительно той из главных центральных осей сечения, вокруг которой будет происходить поворот поперечных сечений после достижения нагрузкой критического значения.

Коэффициент φ изменяется в диапазоне 0≤φ≤1, зависит ,как уже говорилось, как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆λ=10.

Проверка устойчивости.
Подбор сечения.
Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ[σ]А.

Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции , который в свою очередь включен в формулу гибкости , от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:

1 попытка: задаемся φ1 из средней зоны таблицы, находим , определяем размеры сечения, вычисляем , затем гибкость , по таблице определяем и сравниваем со значением φ1 . Если , то:

2 попытка: принимаем , находим , определяем размеры сечения, вычисляем , затем гибкость , по таблице определяем , и если , то:

3 попытка: принимаем , находим , определяем размеры сечения, вычисляем , затем гибкость , по таблице определяем , и т.д.

Расчет сжатых стержней на устойчивость

До сих пор мы рассматривали методы определения напряжений и перемещений, возникающих в стержнях и соответственно, занимались оценкой их прочности и жесткости. Однако оказывается, что соблюдение условий прочности и жесткости еще не гарантирует способности конструкций выполнять, предназначенные им функции в эксплуатационных режимах. Наряду с выполнением условий прочности и жесткости, необходимо обеспечить и устойчивость конструкций.

При неизменной схеме нагружения, под устойчивостью понимается свойство способности системы сохранять свое первоначальное равновесное состояние. Если рассматриваемая система таким свойством не обладает, то она называется неустойчивой, а ее равновесное состояние - неустойчивым состоянием.

При неизменной схеме нагружения, в процессе роста интенсивности нагрузок, явление перехода системы от одного равновесного состояния к другому равновесному состоянию, называется потерей устойчивости системы. Значения внешних сил, при которых происходит потеря устойчивости, называются критическими.

В некоторых случаях при потере устойчивости, система, переходя в новое устойчивое равновесное состояние, продолжает выполнять свои функции. Однако в подавляющем большинстве случаев, потеря устойчивости системы сопровождается возникновением больших перемещений, пластических деформаций или ее полным разрушением. Поэтому сохранение исходного (расчетного) равновесного состояния системы является важной задачей и одной из основных проблем сопротивления материалов.

Основная задача теории устойчивости заключается в определении критического значения внешних сил и ограничение их величин таким образом, чтобы исключить возможность потери устойчивости заданной системы в эксплуатационных режимах.

Пусть вертикальный стержень закреплен нижним концом, а на свободном верхнем конце центрально приложена продольная сила Р (рис. 7.1). На начальном этапе нагружения равновесное состояние системы определяется как простое продольное сжатие, так как на данном этапе нагружения в поперечных сечениях стержня, за исключением продольной силы, остальные силовые факторы равны нулю. При дальнейшем росте внешней силы Р, обнаруживается, что при некотором ее значении P = P_KP , стержень изогнется. Так как явление изгиба тесно связано с действием изгибающих моментов, возникающих в поперечных сечениях стержня, можем утверждать, что при P = P_KP происходила смена формы равновесного состояния системы. Если на начальном этапе нагружения P < P_KP , равновесное состояние вертикального стержня определялось как простое сжатие, то при P > P_KP сжатие сопровождается изгибом. Это означает, что при P = P_KP происходила потеря устойчивости системы.

Заметим, что в данном случае, смена формы равновесного состояния сопровождается и сменой формы деформирования: в докритическом - прямолинейная форма деформирования, в закритическом - криволинейная, а в критическом - смешанная форма.

Заметим также, что для гибких стержней потеря устойчивости может наступить при напряжениях, значительно меньших предела прочности материалов. Поэтому расчет стержней должен выполняться при условии, что сжимающие напряжения не превышают критического значения с точки зрения потери их устойчивости:

где Р_KP - значение сжимающей силы, при котором стержень переходит из прямолинейного состояния равновесия к криволинейному; F - площадь сечения стержня.

Изучение устойчивости стержней начнем с простейшей задачи о стержне с двумя шарнирно опертыми концами при действии центрально сжимающей силы Р (рис. 7.2).

Впервые эта задача была поставлена и решена Л.Эйлером в середине ХVIII века и носит его имя.

Рассмотрим условия, при которых происходит переход от центрально сжатого состояния к изогнутому, т.е. становится возможной криволинейная форма оси стержня при центрально приложенной сжимающей силе Р. Предполагая, что изгиб стержня будет происходить в плоскости минимальной жесткости, записывая дифференциальное уравнение упругой линии балки и ограничиваясь рассмотрением только малых перемещений, имеем:

где I_x - минимальный момент инерции сечения.

Для определения выражения изгибающего момента M_x (z), действующего в поперечном сечении стержня, расположенном на расстоянии z от начала системы координат, применяя метод сечений к системе, изображенной на рис. 7.2 и рассматривая равновесие отсеченной части системы, расположенной левее от заданного сечения, получим:

При положительном прогибе в выбранной системе координат знак “минус” означает, что момент является отрицательным

Введем следующее обозначение:

Тогда уравнение (7.2) преобразуется к виду:

Решение (7.5) записывается в виде:

Постоянные С₁ и С₂ определяются из граничных условий задачи:

y (0) = 0; y (l) = 0.

Из первого условия вытекает, что С₂ = 0, а из второго получается, что либо С₁ = 0 (что нам неинтересно, т.к. в этом случае y (z) º 0), либо

sin kl = 0. (7.7)

Из (7.7) следует, что kl = pn, где n - произвольное целое число. Учитывая (7.4), получаем:

Это означает, что для того, чтобы центрально сжатый стержень принял криволинейную форму, необходимо, чтобы сжимающая сила была равна какому-либо значению из множества Р_n по (7.8). Наименьшее из этих значений называется критической силой Р_KP и будет иметь место при n = 1:

Эта сила носит название первой критической эйлеровой силы.

Следовательно, согласно (7.6) при Р = Р_KP выражение прогибов можно записать в следующем виде:

Из (7.10) видно, что прогибаться стержень будет по синусоиде. Графики функций прогибов y (z) при различных n изображены на рис. 7.3.

Из (7.9) видно, что критическая с точки зрения устойчивости сила зависит от жесткости стержня и его длины, но никак не зависит от прочностных свойств материала стержня, т.е. два стержня одинаковой длины с идентичными граничными условиями их закрепления, изготовленных из различных материалов, но имеющих одинаковую изгибную жесткость, теряют устойчивость при одном и том же значении сжимающей силы. В этом заключается значительная разница между проверкой прочности стержня на сжатие и растяжение и проверкой на устойчивость.

При изменении условий закрепления концов стержня необходимо решение дифференциального уравнения его изгиба, но уже в виде:

Анализ этих решений говорит о том, что все они могут быть представлены в следующем виде:

где m - коэффициент приведения длины. Он показывает, во сколько раз следует изменить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась бы критической силе стержня длиной l в рассматриваемых условиях закрепления. На рис. 7.4 показано несколько видов закрепления стержня и указаны соответствующие значения коэффициента m.

7.2. Границы применимости решения Эйлера.
Формула Ясинского

Как показали опыты, решение Эйлера подтверждалось не во всех случаях. Причина состоит в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень работает в пределах упругих деформаций по закону Гука. Следовательно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности. В связи с этим найдем границы применимости решения Эйлера:

где - радиус инерции сечения. Если стержень имеет одинаковые опорные закрепления в двух взаимно перпендикулярных плоскостях инерции, то при определении значения критической силы и критического напряжения, необходимо брать наименьшее значение момента инерции и, соответственно, радиуса инерции поперечного сечения.

Введем понятие гибкости стержня:

Тогда (7.13) принимает вид:

Из (7.14) следует, что напряжение s_КР возрастает по мере уменьшения гибкости стержня. Заметим, что стержень, имеющий неодинаковые опорные закрепления в главных плоскостях и, следовательно, неодинаковые приведенные длины, теряет устойчивость в той главной плоскости, в которой гибкость стержня имеет наибольшее значение.

Формула Эйлера неприемлема, если напряжения s_КР > s_П, где s_П - предел пропорциональности. Приравнивая (7.14) к пределу пропорциональности, получим предельное значение гибкости:

Если l > l_ПРЕД , то формулу Эйлера можно применять. В противном случае ею пользоваться нельзя. Для стали Ст.3 l_ПРЕД = 100.

В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится нелинейной. В связи с этим, в этих случаях пользуются эмпирическими зависимостями. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:

где a, b - постоянные, зависящие от материала, так для стали Ст.3 a = 3,1×10 5 кН/м 2 , b = 11,4×10 2 кН/м 2 .

Как правило, основная проблема при расчете сжатых стержней состоит в том, чтобы сжимающие напряжения s не превышали бы критических значений по устойчивости s_КР , т.е.

При продольном изгибе центрально сжатый стержень теряет несущую способность, когда напряжения в его поперечных сечениях достигают критических значений. Поэтому необходимо ввести в расчет коэффициент запаса устойчивости n по отношению к критическим напряжениям, с помощью которого и определяется допускаемое напряжение при расчете на устойчивость:

При расчете же стержней на растяжение применяют условие s < R, где R - расчетное сопротивление на растяжение.

Для унификации расчетов на растяжение и сжатие введем соотношение правых частей двух последних неравенств:

откуда . И тогда (7.17) можно записать так: s < jR.

Величина j носит название коэффициента уменьшения расчетного сопротивления при расчете на сжатие и является функцией от гибкости стержня l (табл. 5).

Таким образом, окончательно формула для расчета стержней на устойчивость принимает следующий вид:

Несмотря на простоту выражения (7.19) расчет сжатых стержней производится, как правило, в несколько этапов. Это связано с тем, что величина j зависит от формы и размеров сечения, поэтому не может быть назначена заранее. В связи с этим, подбор сечения осуществляют итеративно, постепенно приближаясь к тому, чтобы разница между напряжением сжатия s и расчетным сопротивлением на растяжение R не превышала бы 3-5%.

Расчет на устойчивость по аналитическим зависимостям

Расчетом на устойчивость определяют величину сжимающей критической нагрузки P_кр, при которой прямолинейный сжатый стержень оказывается в опасном (критическом) состоянии безразличного равновесия, т.е. переходит к новой криволинейной форме равновесия. Отношение критической нагрузки к действующей величине P называется коэффициентом запаса устойчивости n_у.

Запас устойчивости n_у, из-за возможной эксцентричности приложения нагрузки, искривления стержня и неоднородности, всегда принимается несколько больше коэффициента запаса статической прочности n_σ. Рекомендуемые величины коэффициента запаса устойчивости для стальных стоек находятся в пределах n_у =1,5÷3.

Расчет на устойчивость можно проводить как по аналитическим зависимостям, так и по коэффициентам снижения основного допускаемого напряжения.

Различают три вида расчетов на устойчивость по аналитическим зависимостям: проверочный расчет, определение допускаемой нагрузки и проектировочный расчет.

1) Проверочный расчет. Цель этого расчета в оценке устойчивости рассчитываемого элемента при действии на него заданной внешней нагрузки.

Расчет проводим в несколько этапов.

а). Вычисляем гибкость стержня λ и предельное значение гибкости λ_пред по формулам:

μ - коэффициент приведения длины, учитывающий характер закрепления концов стержня;

l – длина стержня;

I_min- минимальный главный центральный момент инерции сечения;

σ_пц – предел пропорциональности материала стержня;

E – модуль упругости материала стержня.

б). Определяем критическую нагрузку Р_кр.

В зависимости от гибкости сжатые стержни условно делим на три группы:

- стержни большой гибкости (λ≥ λ_пред), для которых критическую нагрузку Р_кр определяем по формуле Эйлера:

- стержни средней гибкости (λ₀≤λ≥ λ_пред), для которых расчет на устойчивость проводим по формуле Ясинского:

где σ_кр – критические сжимающие напряжения;

F – площадь поперечного сечения стержня;

σ_тс – предел текучести материала стержня на сжатие.

Либо расчет проводим по формуле Кармана:

где I₁, I₂ - моменты инерции площадей зон догрузки и разгрузки относительно нейтральной оси.

I – момент инерции всего сечения относительно главной центральной оси;

E_пр - приведенный модуль или модуль Кармана;

E_к- касательный модуль упругости;

Е- модуль упругости.

- стержни малой гибкости (λ₀≤λ), для которых расчет на устойчивость не проводим, а проверяем их прочность на сжатие.

в). Определяем коэффициент запаса устойчивости и сравниваем полученное значение запаса устойчивости с требуемым значением.

2) Определение допускаемой нагрузки. В этом расчете определяем максимально допустимое значение сжимающей силы, при которой будет обеспечен требуемый запас устойчивости n_у. Также как и в проверочном расчете определяем значение критической нагрузки Р_кр. Затем по найденному значению критической нагрузки Р_кр и заданному значению запаса устойчивости n_у определяем допустимую величину сжимающей нагрузки .

3) Проектировочный расчет. Расчет заключается в определении требуемых размеров стержня, при которых он будет обладать требуемым запасом устойчивости.

Поскольку размеры сечения неизвестны и, следовательно, гибкость стержня не может быть определена, то расчет вначале ведем по формуле Эйлера, предполагая, что гибкость стержня не меньше предельной. В этом случае условие устойчивости имеет вид:

Учитывая, что , определяем потребный минимальный момент инерции сечения:

Задаемся формой и размерами сечения и вычисляем радиус инерции i, гибкость стержня λ и предельное значение гибкости λ_пред по формулам:

Если при выбранных размерах λ₀≤λ≥ λ_пред, то расчет на устойчивость повторяем. В этом случае потребную площадь поперечного сечения определяем по формуле:

Критические напряжения σ_кр определяем либо по формуле Ясинского:

либо по формуле Кармана:

Определить запас устойчивости продольно нагруженной стойки (рис. 11.28а) при двух вариантах ее изготовления из двух швеллеров №5 и двух полос (рис. 11.28б, в). При расчете принять P=200 кН. Материал стойки- сталь с механическими характеристиками σ_пц=220 МПа, σ_т=280 МПа, Е=2×10 5 МПа.

I. Рассмотрим первое расположение швеллеров, приведенное на рисунке 10.28б.

1. По ГОСТ 8240-72 для швеллера №5 находим:

F_шв = 6,16×10 -4 м 2 ,

I_{z шв} = 22,8×10 -8 м 4 , i_{z шв} = 1,92 10 -2 м,

I_{y1 шв} = 5,61×10 -8 м 4 , i_{y шв} = 0,954 10 -2 м.

2. Вычислим моменты инерции сечения, показанного на рис. 10.28б, относительно осей z и y.

3. Определим гибкость стержня.

Минимальным оказался момент инерции относительно оси y, следовательно:

, где μ = 2 для жесткой заделки стержня с одной стороны.

Определим предельное значение гибкости:

4. Так как λλ_пред, формула Эйлера неприменима, поэтому критическую силу вычисляем по зависимости Ясинского:

P_кр = σ_кр×F = 223,8 ×10 6 ×20,72×10 -4 = 463,7 кН, где

5. Определим коэффициент запаса устойчивости:

, что меньше требуемого запаса устойчивости на %

II. Рассмотрим второе расположение швеллеров, приведенном на рисунке 10.28в.

1. Очевидно, что момент инерции сечения относительно оси z не изменится I_z = 112×10 -8 м 4

В этом случае стойка практически равноустойчива во всех направлениях I_z ≈ I_y.

2. Определим гибкость стержня.

Минимальным оказался момент инерции относительно оси y, следовательно:

, где μ = 2, так как стержень жестко заделан с одной стороны.

3. Так как λλ_пред, критическую силу вычислим по эмпирической зависимости Ясинского:

P_кр = σ_кр×F = 235,5 ×10 6 ×20,72×10 -4 = 487 кН, где

4. Определим коэффициент запаса устойчивости:

, что меньше требуемого запаса устойчивости на

Определить напряжение и проверить прочность тяги 6-7 двойного управления рулем высоты при действии на каждую штурвальную колонку (рис. 10.29) расчетной нагрузки Р р =1,8 кН в двух направлениях, если H=0,8 м, r=0,08 м, l_6-7=1,2 м. Тяга выполнена трубчатого сечения D×d=45×40 мм из алюминиевого сплава с характеристиками σ_в=440 МПа, Е=7×10 4 МПа, σ_пц=350 МПа.

1. Определим усилия в стержнях.

При изменении направления усилия на штурвальную колонку усилия в тягах только изменят знак.

2. Определим геометрические характеристики сечения тяг.

Для кольцевого сечения:

осевой момент инерции-

3. Определим напряжение в тяге 6-7:

4. Проверим прочность тяги 6-7 на растяжение:

а) запишем условие прочности:

б) определим коэффициент избытка прочности:

5.Проверим прочность тяги 6-7 на сжатие:

а) Определим гибкость стержня.

, где μ = 1, так как стержень шарнирно оперт с обоих краев.

б) Определим предельное значение гибкости:

Так как λ>λ_пред , то критическую силу определим по формуле Эйлера:

в) Определим коэффициент запаса устойчивости:

3.2 Расчет на устойчивость по коэффициентам уменьшения основного допускаемого напряжения

В случае стержней с большой гибкостью опасным состоянием следует считать момент возникновения в сжатом стержне напряжения равного σ_кр. В этом случае условие устойчивости можно записать:

где [σ]_у- допускаемое напряжение на устойчивость, определяемое по формуле:

где n_у- коэффициент запаса устойчивости.

Введем обозначение . Соответственно, допускаемое напряжение на устойчивость:

где φ - коэффициент снижения допускаемого напряжения на сжатие;

[σ]_с – допускаемое напряжение на осевое сжатие стержня.

Коэффициент φ определяет степень снижения допускаемого напряжения при подольном изгибе. Поскольку коэффициент зависит от критического напряжения, то очевидно, что он зависит от гибкости стержня и механических характеристик материала. Следовательно, расчет на устойчивость сжатых стержней можно выполнять по форме как расчет на осевое сжатие, введя пониженное допускаемое напряжение [σ]_у.

Условие устойчивости можно записать:

Значения коэффициентов φ для продольного изгиба центрально сжатых стержней из сталей приведены в таблице 10.3.

Гибкость, λ	Коэффициенты φ для сталей с допускаемым напряжением на сжатие [σ]_с, МПа
0,988	0,987
0,967	0,962
0,939	0,931
0,906	0,894
0,869	0,852
0,827	0,805
0,782	0,754
0,734	0,686
0,665	0,612
0,599	0,542
0,537	0,478
0,479	0,419
0,425	0,364
0,376	0,315
0,328	0,276
0,290	0,244
0,259	0,218
0,233	0,196
0,210	0,177
0,191	0,161
0,174	0,147
0,16	0,135

Подчеркнем, что хотя расчет по форме это расчет на сжатие, но по существу это расчет на устойчивость, обеспечивающий работу стержня с коэффициентом запаса устойчивости. Раличают два вида расчета на устойчивость: проверочный и пректировочный.

1) Проверочный расчет.

Если задана сжимающая сила, а также геометрические характеристики стержня то проверка прочности на устойчивость каких либо затруднений не вызывает. Прежде всего, определяем наименьший осевой момент инерции I_min , площадь сечения F и мининимальный радиус инерции:

а также гибкость:

Затем, зная гибкость, находим по таблице коэффициентφ и проверяем условие устойчивости:

2) Проектировочный расчет.

Более сложной задачей оказывается подбор сечения при заданной длине и сжимающей силе. Дело в том, что коэффициент φ зависит от гибкости стержня λ, а гибкость неизвестна, поскольку неизвестно сечениеение. В таком случае расчет выполняют методом последовательных приближений. Исходим из условия устойчивости:

Из неравенства определяем потребную площадь сечения:

Кроме искомой площади в последнем соотношении неизвестным является также коэффициент φ. Поэтому при подборе сечения приходится пользоваться методом последовательных приближеня величину коэффициента φ. Обычно на первом шаге принимаем φ₁=0,5‑0,6. При принятом φ₁определяем F и подбираем конфигурацию сечения, для которого определяем I_min, i_min, и λ. Определяем новое значение φ₁´. Если φ₁´ зачительно оличается от φ₁, то расчет поворяют при . В результате второй итерации определяют φ₂´. Если требуется третья итерация расчет повторяют при . Обычно на практике удается обойтись двумя-тремя итерациями.

В стержне фермы возникает сжимающая сила P = 352 кН. Поперечное сечение стержня состоит из двух равнополочных уголков, расположенных тавром и соединенных между собой таким образом, что их совместная работа, как единого стержня, обеспечена. Материал стержня сталь Ст.3 (E=2,1×10 5 МПа, [σ]_с=160 МПа, [σ]_пц=220 МПа), длина стержня l =5,31 м, концы стержня считать закрепленными шарнирно.

Подобрать размеры поперечного сечения стержня. Определить коэффициент запаса устойчивости стержня при принятых размерах поперечного сечения.

Расчет ведем по коэффициентам продольного изгиба:

1. Первое приближение. Примем φ₁ =0,6.

Требуемая площадь сечения одного уголка:

F₁ = F/2 = 1,84×10 -3 м 2

По ГОСТ 8509-72 уголок 100×100×10 имеет F₁ = 1,92×10 -3 м 2 . Минимальный радиус инерции сечения i_min= i_x = 3,05×10 -2 м (очевидно, что для принятого сечения I_x < I_y).

, здесь μ=1, так как стержень шарнирно оперт.

По таблице 10.3 определим φ:

Значение значительно отличается от предварительно принятого φ.

2. Второе приближение.

Уголок 125×125×12-по ГОСТ 8509-72 имеет F=2,89×10 -3 м 2 , i_min= i_x = 3,82×10 -2 м

Определим гибкость стержня:

По таблице 10.3 - φ₂≈0,376.

Определим действующее напряжение сжатия:

Определим допускаемое напряжение по условиям устойчивости:

Следовательно, стержень будет перегружен на 1,16%. Такая перегрузка нежелательна, поэтому рассмотрим еще один вариант. Примем уголок с меньшей площадью сечения, но с большим радиусом инерции, что приведет к уменьшению гибкости, а, следовательно, к повышению φ и [σ]у.

3. Третье приближение.

Примем уголок 140×140×9 с F=2,47×10 -3 м 2 , i_min= i_x = 4,34×10 -2 м;

По таблице 10.3 - φ₂≈0,468

Стержень будет недогружен на 5 %.

4. Определим коэффициент запаса устойчивости при принятых размерах сечения.

Так как λ≥λ_пред, то для определения критических напряжений применим формулу Эйлера:

Определим запас устойчивости:

Конструкция цилиндрического гермофюзеляжа самолета, представляющая собой тонкостенную оболочку подкрепленную продольным (стрингера) и поперечным (шпангоуты) набором, изготовлена из алюминиевого сплава Д-16 с пределом текучести σ_тр= 26 кг/мм 2 и μ=0,3. Определить коэффициент запаса по условиям текучести n_т для пяти критериям текучести при следующих условиях нагружения:

а) эксплуатационный изгибающий момент вызывает продольные растягивающие нормальные напряжения в верхних точках фюзеляжа равными σ_x=20 кг/мм 2 ;

б) одновременно с эксплуатационным изгибающим моментом в гермофюзеляжа создается избыточное давление Δp = 0,6 кг/cм 2 , которое вызывает в обшивке продольные σ_x= 4 кг/мм 2 и кольцевые напряжения σ_t= 8 кг/мм 2 ;

в) дополнительно к условиям нагружения приведенным в п. б) на фюзеляж при выполнении маневра действует крутящий момент, который вызывает касательные напряжения в обшивке τ_xt= 8 кг/мм 2 .

В данном случае реализовывается одноосное напряженное состояние (рис. 9.6), для которого для всех критериев текучести эквивалентные напряжения равны:

Следовательно, коэффициент запаса по условиям текучести:

При заданном случае нагружения на внутренней поверхности обшивки гермофюзеляжа реализовывается трехосное напряженное состояние (рис. 9.8).

В продольном направлении действует сумма напряжений от изгибающего момента и от избыточного давления σ_x =20+4 = 24 кг/мм 2 . На внутреннюю поверхность обшивки действует избыточное давление Δp = 0,6 кг/cм 2 , которое вызывает в поверхностных слоях в радиальном направлении нормальное напряжение сжатия σ_r = - 0,006 кг/мм 2

Действующие напряжения являются главными напряжениями: σ₁ = σ_x = 24 кг/мм 2 , σ₂=σ_t= 8 кг/мм 2 , σ₃ = σ_r=0,006 кг/мм 2 .

1. По критерию максимальных главных напряжений:

σ_экв = σ_x

2. По критерию максимальной главной деформации:

3. По критерию суммарной энергии деформации:

4. По критерию максимальных касательных напряжений:

5. По критерию энергии деформации сдвига:

При заданном случае нагружения на внутренней поверхности обшивки гермофюзеляжа реализовывается трехосное напряженное состояние (рис. 9.9).

Дополнительно к напряжениям предыдущего нагружения, приведенному в п. б), действует касательное напряжение τ_xt= 8 кг/мм 2 .

Читайте также: