Расчет внецентренно сжатых стальных элементов
Обновлено: 19.04.2024
Предельные состояния внецентренно растянутых и жестких внецентренно сжатых элементов определяются несущей способностью по прочности или развитием пластических деформаций, а гибких внецентренно сжатых — потерей устойчивости.
Расчет на прочность. Предельные состояния по прочности внецентренно растянутых (растянуто-изогнутых) и внецентренно сжатых (сжато-изогнутых) элементов конструкций при динамических воздействиях, а также элементов конструкций, выполненных из сталей высокой прочности с расчетным сопротивлением R>580 МПа, определяются достижением наибольшими фибровыми напряжениями расчетного сопротивления. Их расчет выполняется по упругой стадии работы материала по формуле
Для внецентренно сжатых и внецентренно растянутых элементов из пластичных сталей с пределом текучести до 580 МПа при действии статических нагрузок предельное состояние по прочности определяется с учетом развития пластических деформаций.
Развитие пластических деформаций при наличии момента и продольной силы так же, как ив изгибаемых элементах, приводит к образованию шарнира пластичности, но при этом положение нейтральной оси в процессе развития пластических деформаций смещается. При увеличении момента и продольной силы на одной из сторон стержня фибровые напряжения достигают предела текучести и затем останавливаются в своем развитии.
Напряжения в прочих фибрах (угол наклонной части эпюры напряжений) продолжают расти, пока, наконец, напряжения на другой стороне стержня не достигнут предела текучести, после чего пластичность распространяется на все фибры сечения, Очевидно, что разность площадей эпюр напряжений, умноженная на , равна предельной продольной силе
где и —площади частей сечения.
Площадь определяет одну составляющую пары изгибающего момента; такая же площадь на другой стороне сечения должна определять вторую составляющую этой пары. Отсюда предельный момент
где е — расстояние между центрами площадей .
Таким образом, в пластической стадии напряжения от продольной силы и момента можно условно разделить. Напряжения от продольной силы занимают среднюю часть — сечения =A— 2A2, а напряжения от момента — края на площадях А2.
При развитии шарнира пластичности соотношение предельных продольных сил, отвечающих наличию момента и его отсутствию определяется отношением , а соотношение предельных моментов, отвечающих наличию продольной силы и ее отсутствию , определяется отношением .
Для прямоугольного сечения связь между этими отношениями выражается параболой
Для двутавровых сечений эта зависимость ближе к линейной и может быть выражена
где а — коэффициент, определяемый характером распределения материала по сечению двутавра.
Аналогичный подход может быть использован и при работе стержня на совместное действие двух моментов Мх и Му и нормальной силы.
Образование шарнира -пластичности приводит к неограниченному росту перемещений. Для обеспечения эксплуатационной пригодности конструкций проверяют прочность элементов при совместном действии изгиба и осевой силы, как и изгибаемых элементов (см. п. 4 настоящего параграфа), по критерию ограниченных пластических деформаций
Коэффициенты п, сх и учитывают степень развития пластических деформаций и зависят от формы сечения. Численные значения этих коэффициентов при ε=3 для некоторых типов сечения приведены в прил. 5.
Проверка устойчивости внецентренно сжатых (сжато-изгибаемых) элементов. При приложении сжимающей силы с эксцентриситетом стержень работает как внецентренно сжатый. При одновременном приложении продольной осевой силы и поперечной нагрузки, вызывающей изгиб, стержень будет сжато-изгибаемым. Хотя в том и в другом случае по сечению развиваются напряжения одинакового вида, вызванные продольной силой и моментом, работа стержня в этих случаях несколько отличается главным образом в предельном состоянии при малых гибкостях. Однако в целях упрощения практических методов расчета (в небольшой запас) сжато-изгибаемые стержни при рассмотрении критического состояния потери устойчивости приравниваются к внецентренно сжатым, имеющим эксцентриситет .
Напомним, что даже при осевом приложении нагрузки всегда имеются случайные эксцентриситеты, и поэтому исследованная выше работа центрально сжатых стержней (п. 5 данного параграфа) является по существу работой сжатых стержней с малыми эксцентриситетами. Работа же внецентренно сжатых стержней с большими или малыми эксцентрицитетами не имеет принципиальных отличий; только большие значения эксцентрицитетов и моментов сказываются на работе внецентренно сжатых стоек более ярко, процесс же потери устойчивости остается тождественным.
При внецентренном сжатии с самого начала приложения нагрузки помимо продольной деформации возникает изгиб стержня. Поэтому расчет таких стержней следует проводить по деформированной схеме.
При определении критической (предельной) силы Nu принимаются следующие основные предпосылки:
перемещения считаются достаточно малыми, что позволяет использовать приближенное выражение для кривизны изогнутой оси
относительные деформации в поперечном сечении е следуют гипотезе плоских сечений
связь между нормальными напряжениями а и относительными деформациями для материала устанавливается зависимостью
в процессе возрастания нагрузки и в момент потери устойчивости влияние разгрузки не учитывается, т. е. рассматривается нелинейно упругий материал как в условиях догрузки, так и разгрузки.
Для определения предельной нагрузки Nu применим метод бесконечно малых возмущений в окрестностях состояний равновесия стержня. Для этого рассмотрим некоторое исходное состояние равновесия в точке А. Условия равновесия внешних и внутренних сил и изгибающих моментов в сечениях стержня имеют вид
;
Наряду с этим рассмотрим другое состояние равновесия в точке А1 отличающееся от исходного на бесконечно малую величину перемещения . При этом деформации и напряжения в сечениях получают приращения, равные соответственно и . Условия равновесия внешних и внутренних сил и моментов для нового равновесного состояния в точке получат следующий вид:
;
Вычитая почленно из уравнений уравнения с точностью до бесконечно малых второго порядка, получим условия равновесия для бесконечно малых приращений:
Полученные зависимости справедливы для любой точки кривой состоянии равновесия ОМВ.
Практический интерес представляет решение этих уравнений для точки М максимума кривой ОМВ. В бесконечно малой окрестности точки М сжимающая сила постоянна, в связи с чем имеем . При этом из уравнений получаем:
Из диаграммы работы материала имеем
где Et — касательный, модуль для диаграммы работы материала стержня.
С учетом находим
Подставляя из предыдущей формулы в условия равновесия с учетом, получим:
Определяя из первого уравнения системы величину и подставляя ее во второе уравнение этой системы, получим дифференциальное уравнение для определения Nu в следующем виде:
,
где —момент инерции приведенного с учетом касательного модуля сечения относительно его собственной центральной оси.
При решении практических задач форма изогнутой оси обычно принимается по полуволне синусоиды
В этом случае условия равновесия достаточно рассмотреть только в наиболее напряженном (срединном) сечении стержня. При этом из решения уравнения с учетом находим
Для определения приведенной жесткости стержня необходимо знать эпюру напряжений в наиболее нагруженном сечении стержня. Зависимость можно записать в виде
где Еs — секущий модуль.
Тогда, рассматривая систему получим дифференциальное уравнение изгиба внецентренно сжатого стержня
Таким образом, значения предельных параметров в точке М определяются в результате совместного решения двух уравнений и для срединного сечения стержня.
В соответствии с изложенным разработана методика расчета на устойчивость внецентренно сжатых и сжато-изогнутых элементов, установленная в нормах на проектирование стальных конструкций.
Проверка устойчивости элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии (изгибная форма потери устойчивости), производится по формуле
где — коэффициент снижения расчетных напряжений при внецентренном сжатии определяется в зависимости от условной гибкости и приведенного эксцентрицитета , определяемого по формуле
где η— коэффициент влияния формы сечения; m=eA/Wc—относительный эксцентрицитет (отношение эксцентрицитета к радиусу ядра сечения);Wc — момент сопротивления для наиболее сжатого волокна; e=M/N — эксцентрицитет приложения нормальной силы; М — расчетный момент, принимаемый в зависимости от условий закрепления стержня по концам и вида эпюры моментов.
Коэффициент влияния формы сечения учитывает степень ослабления сечения при потере устойчивости пластическими деформациями. При сжатии двутаврового сечения с эксцентрицитетом в плоскости стенки текучесть быстро распространяется по толщине полки и сечение превращается в тавровое. Резкое ослабление сечения в этом случае учитывается коэффициентом η>1. В случае незначительного ослабления сечения пластическими деформациями коэффициент ту ηвц получаются меньше, чем для сплошностенчатых стержней.
Если сжимающая сила приложена не в центре изгиба, то стержень не только изгибается, но и закручивается и теряет устойчивость по изгибно-крутильной форме. Переход части сечения в пластическую стадию работы смещает центр изгиба и также способствует закручиванию стержня. Эта форма потери устойчивости наиболее характерна для тонкостенных незамкнутых сечений, обладающих низкой крутильной жесткостью.
Во внецентренно сжатых элементах, у которых жесткости в обоих главных направлениях различны и момент действует в плоскости наибольшей жесткости, возможна потеря устойчивости в плоскости, перпендикулярной действующему моменту. Проверка устойчивости таких стержней из плоскости действия момента согласно СНиП П-23-81 производится по формуле
где — коэффициент продольного изгиба, принимаемый как для центрально сжатого стержня в зависимости от гибкости (см. прил. 7); с — коэффициент, учитывающий изгибно-крутильную форму потери устойчивости и зависящий от относительного эксцентрицитета и формы сечения.
4.5. Расчет внецентренно - сжатых элементов
При расчете таких элементов необходимо обеспечить их несущую способность, потеря которой возможна как вследствие потери прочности, так и за счет потерн устойчивости (в носкости действия изгибающего момента или из его плоскости).
Расчет на прочность внецентренно-сжатых, сжато-изгибаемых, внецентренно-растянутых и растянуто-изгибаемых элементов из стали с пределом текучести до 530 МПа (5400 кгс/кв.см), не подвергающихся непосредственному воздействию динамических нагрузок, при и0,1 следует выполнять по формуле
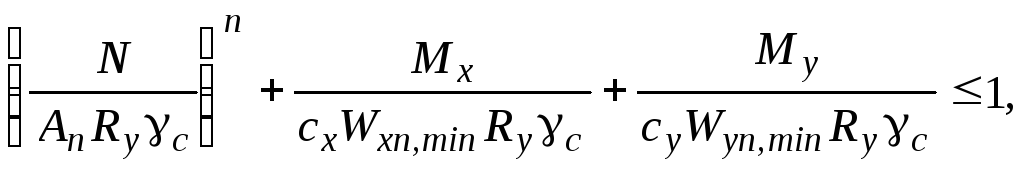
где и- абсолютные значения соответственно продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании;
и - коэффициенты, принимаемые по прил. 5 СНиII-23-81*.
Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии, следует выполнять по формуле
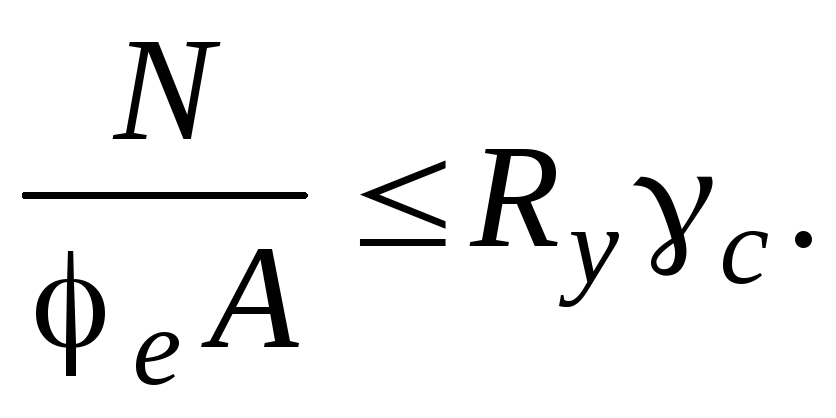
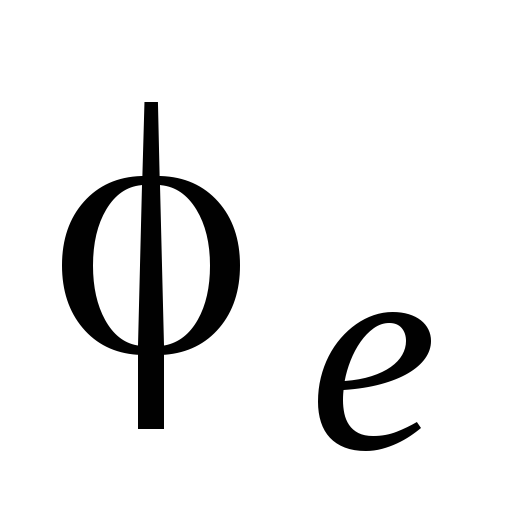
В формуле коэффициент следует определять:
а) для сплошностенчатых стержней по табл. 74 СНиII-23-81*в зависимости от условной гибкости и приведенного относительного эксцентриситетаопределяемого по формуле
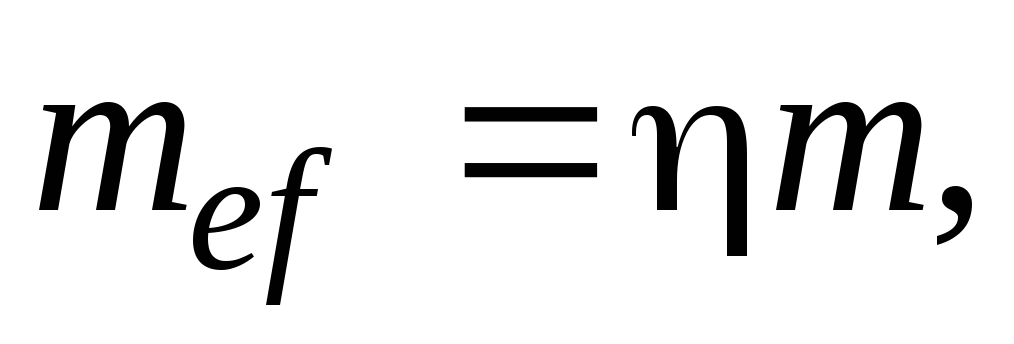
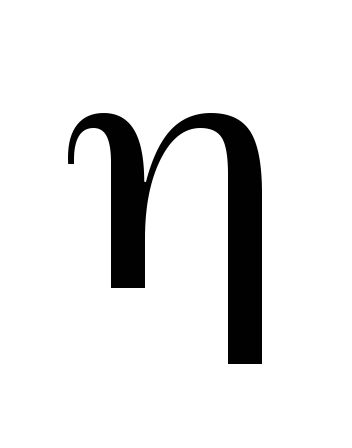
где - коэффициент влияния формы сечения, определяемый по табл. 73; СНиII-23-81*.
- относительный эксцентриситет (здесь - эксцентриситет;- момент сопротивления сечения для наиболее сжатого волокна);
б) для сквозных стержней с решетками или планками, расположенными в плоскостях, параллельных плоскости изгиба, по табл. 75 СНиII-23-81*.в зависимости от условной приведенной гибкости (по табл. 7 СНиП II-23-81*.) и относительного эксцентриситетаопределяемого по формуле
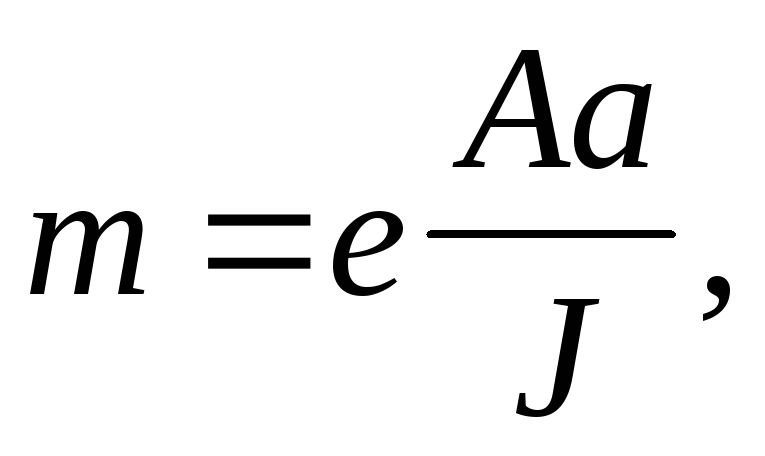

где - расстояние от главной оси сечения, перпендикулярной плоскости изгиба, до оси наиболее сжатой ветви, но не менее расстояния до оси стенки ветви.
При вычислении эксцентриситета значенияиследует принимать согласно требованиям п. 5.29 СНиП II-23-81*.
Расчет на устойчивость не требуется для сплошностенчатых стержней при 20 и для сквозных стержней при20, в этих случаях расчет следует выполнять как для изгибаемых элементов.
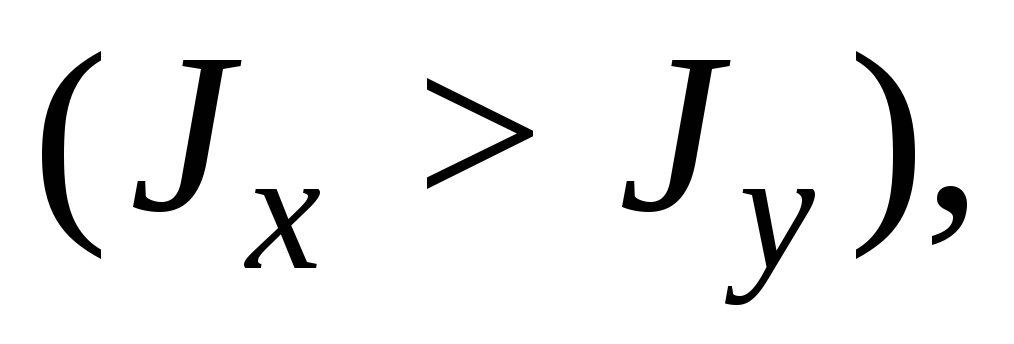
Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента при изгибе их в плоскости наибольшей жесткости совпадающей с плоскостью симметрии, следует выполнять по формуле


где - коэффициент, вычисляемый согласно требованиям п. 5.31 СНиП II-23-81*;
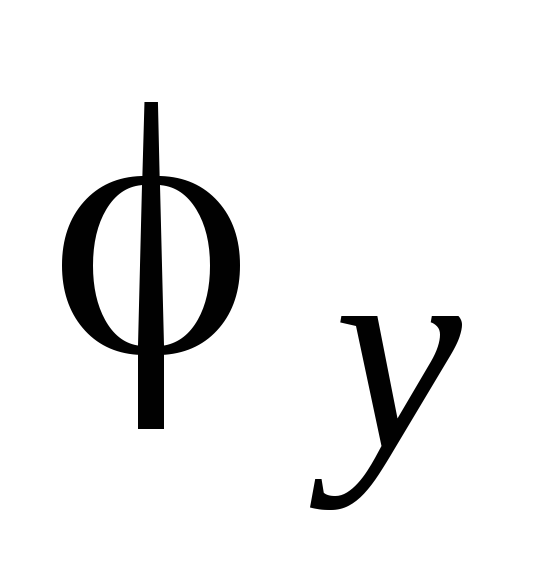
- коэффициент, вычисляемый согласно требованиям п. 5.3 СНиП II-23-81*.

Коэффициент в формуле следует определять:
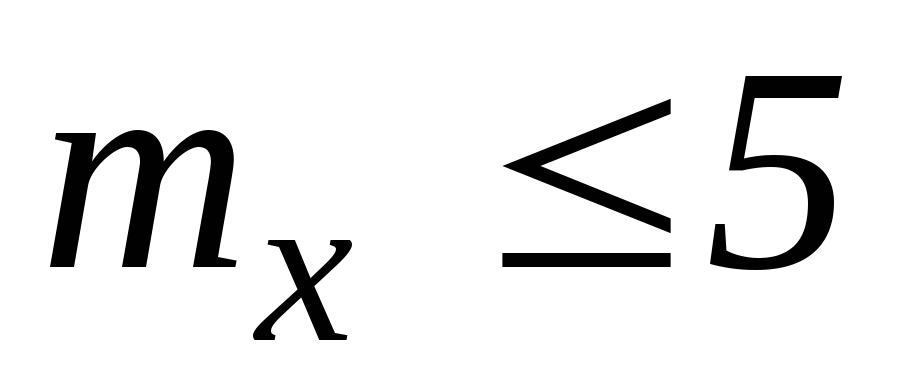
при значениях относительного эксцентриситета по формуле
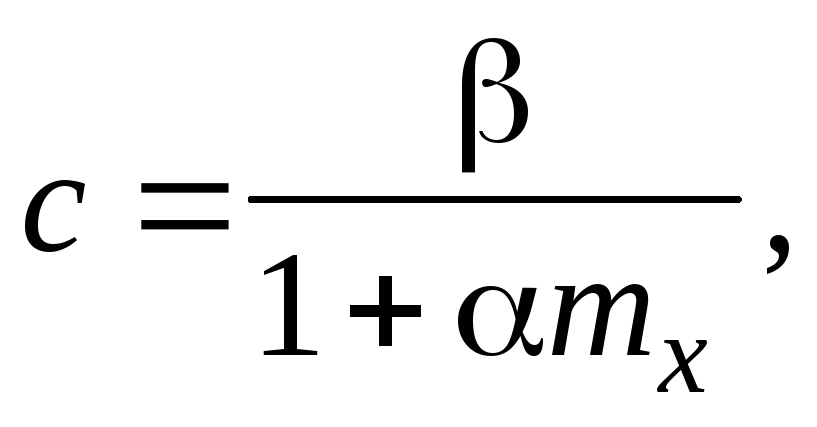
где и- коэффициенты, принимаемые по табл. 10 СНиП II-23-81*.
Контрольные вопросы
Как производится расчет центрально-сжатых.
Приведите расчет общей устойчивости центрально-сжатых элементов (понятие плоскости наименьшей жесткости).
4.Понятие о расчете внецентренно- сжатых колонн
В отличие от центрального сжатия при внецентренном сжатии напряжения в поперечном сечении распределяются неравномерно. При этом возможны три основных случая :
а)σ min>0, σmax > 0;
б)σ min=0, σmax > 0;
При внецентренном сжатии на продольный изгиб оказывает влияние изгибающий момент, и поэтому размеры сечения внецентренно сжатых элементов увеличивают в направлении действия момента.
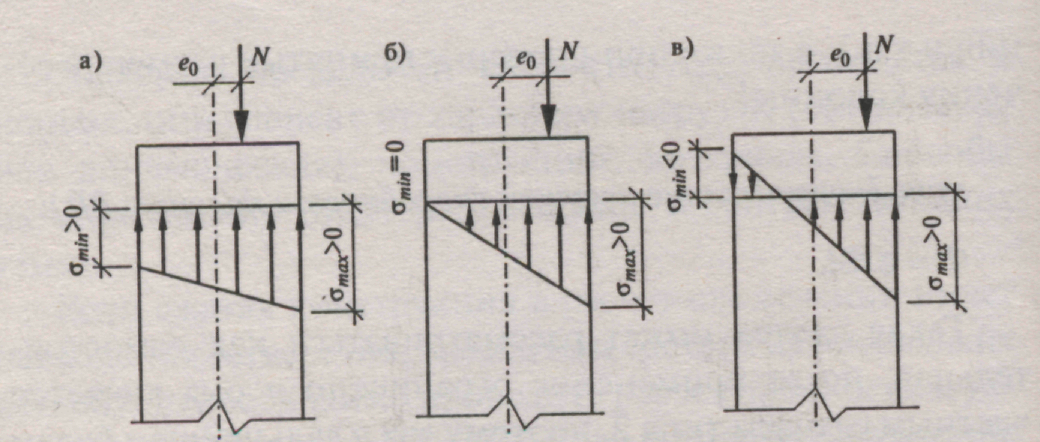
Распределение напряжений при внецентренном сжатии
Расчет внецентренно сжатых колонн зависит от материала. Внецентренно сжатые железобетонные и каменные колонны необходимо рассчитывать не только на прочность, общую устойчивость, но в некоторых случаях на раскрытие трещин.
Тема: «Особенности расчета стальных колонн под нагрузкой. Общий порядок расчета »
Цель урока: Дать основные понятия расчета и конструирования стальных колонн.
1.Особенности работы стальной колонны. 2 .Расчет центрально-сжатой колонны сплошного сечения под нагрузкой.
3.Правила конструирования центрально – сжатой колонны.
4. Расчет центрально - сжатой колонны сквозного сечения.
1.Особенности работы стальной колонны
Простейшей конструкцией стальных колонн является сплошная колонна постоянного сечения, выполненная из трубы или прокатного двутавра. Выполняются сплошные колонны составного сечения из прокатных элементов: двух швеллеров, уголков и других комбинаций.

Сечения сплошных колонн: а) прокатный двутавр; б) сварной двутавр; е) труба; г) сечение из двух швеллеров; д) сечение из двух уголков
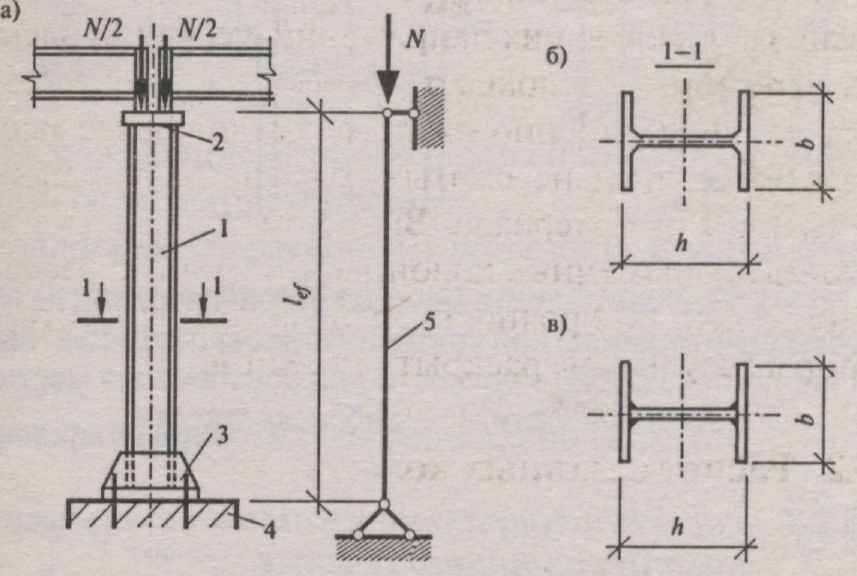
Сплошная центрально-сжатая колонна: а) конструкция;
б) сечение из прокатной двутавровой балки;
в) двутавровое сечение, сваренное из листов;
1 — стержень колонны; 2 — оголовок колонны; 3 — база колонны
4 — фундамент; 5 — расчетная схема
Несущая способность стальных колонн может быть исчерпана от потери местной устойчивости, для исключения этого явления применяется постановка поперечных ребер жесткости конструктивное увеличение толщины листов, из которых изготавливается колонна.
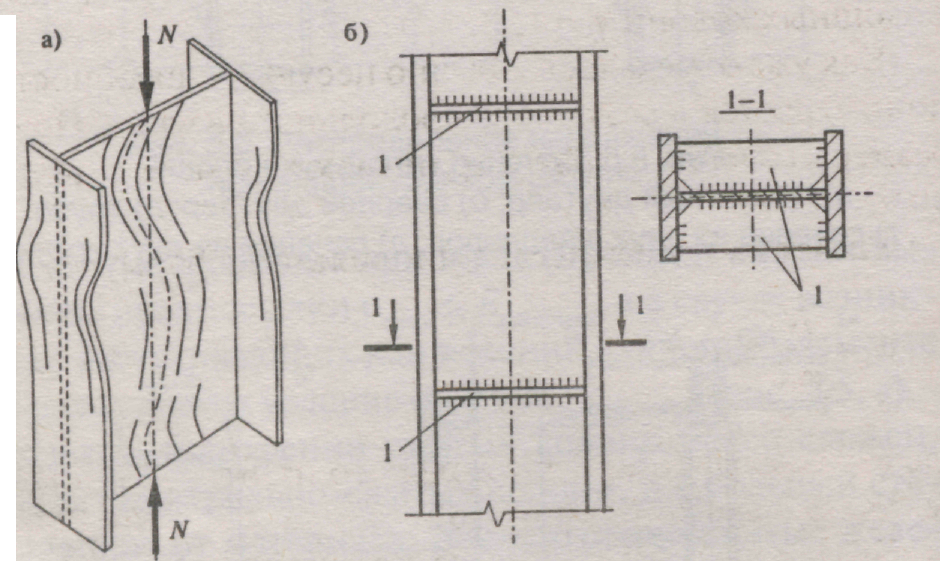
Потеря местной устойчивости: а)схема потери местной устойчивости сварного двутавра б)постановка ребер жесткости для обеспечения местной устойчивости; 1 — ребра жесткости
2.Расчет центрально-сжатых стальных колонн сплошного сечения
При расчете стержня колонны необходимо выполнение следующих расчетов: по прочности, по потере общей устойчивости, а также при этом необходимо ограничивать гибкость.
Расчет прочности выполняют по формуле
где σ —нормальное напряжение в сечении колонны;
N — расчетная продольная сила;
— площадь сечения нетто, т.е. площадь сечения за вычетом площади ослаблений,
-расчетное сопротивление стали по пределу текучести (таблица 51 СНиП
— коэффициент условия работы, (при расчетах прочности сплошных колонн = 1,1 или по таблица 6 СНиП II-23-81*)
Обычно несущая способность колонн теряется в результате продольного изгиба. Поэтому размеры сечения стержня принимают из расчета на устойчивость.
Расчет на устойчивость выполняют по формуле
где φ — коэффициент продольного изгиба;
А — площадь без учета ослаблений (брутто).
Независимо от расчета на прочность и устойчивость нормы ограничивают наибольшую гибкость стержня колонны, которая должна быть не больше предельной (табл. 19 СНиП II-23-81*).
Проверка гибкости выполняется по формуле
где — расчетная длина колонны
i-радиус инерции сечения.
Общий порядок подбора сечения стержня колонны (тип 1)
1.Определяют нагрузку на колонну
2.Устанавливают расчетную схему.
3.В зависимости от расчетной схемы находят расчетную длину колонны по формуле
=μ l где μ, — коэффициент расчетной длины);
l-геометрическая длина колонны.
4.Назначают тип поперечного сечения стержня колонны: труба, прокатный двутавр, составное сечение из прокатных профилей и т.п.
5.Принимают сталь для колонны; выбор стали зависит от конструкции колонны, величины нагрузок, климатического района и условий эксплуатации (отапливаемое или не отапливаемое здание), экономического обоснования и т.д.
6.Для принятой стали определяют расчетное сопротивление по пределу текучести (таблица 51 СНиП II-23-81*).
7.Определяют коэффициент условия работы колонны (табл. 6 СНиП II-23-81*).
8.Определяют требуемую площадь поперечного сечения стержня. Требуемая площадь сечения находится из формулы:
Так как А и φ неизвестных, то одной из величин необходимо задаться, т.е. принять предварительно, а затем выполнить проверочный расчет. Задаемся гибкостью λ, величина которой не должна превышать (гибкость колонн обычно находится в пределах от 100 до 70), по принятой гибкости устанавливают коэффициент φ (табл.72 СНиП II-23-81*).
9.Определяют требуемый радиус инерции, подставляя в уравнение принятую гибкость:
10.По найденным площади и радиусу инерции, пользуясь сортаментом прокатных элементов, принимают сечение стержня колонны и выписывают фактические характеристики принятого сечения(А, ix,iy ).
Для сварных колонн, выполняемых из стальных листов, сечение колонны следует назначить самостоятельно: высота сечения колонны в виде двутавра принимается обычно в пределах
h= (1/12— 1/20)l; ширина b принимается равной высоте сечения h толщина поясов принимается в пределах 10—40 мм, а толщина стенки = 6—18 мм. Назначенное сечение должно иметь площадь, примерно равную требуемой площади .Наименьший расход металла получается, если на долю поясов приходится около 80% от общей площади поперечного сечения, и соответственно, 20% должно приходиться на стенку:
Полученное сечение колонны может быть изменено при дальнейших расчетах.
11.Проводят проверку принятого сечения и при необходимости выполняют уточнение его размеров.
Проверку устойчивости производят по формуле
Наибольшую гибкость колонны находят по формуле
где -меньший радиус инерции принятого сечения (ix,iy)
В зависимости от и находят действительный коэффициент продольного изгиба φ
12.Независимо от выполненного расчета необходимо, чтобы гибкость колонны не превышала предельной . Предельные гибкости сжатых элементов принимаются (для основных колонн они определяются) по табл. 19 СНиП II-23-81*.
λпред = 180 - 60ά, где коэффициент ά = N/φA ≥0,5).
3. Правила конструирования центрально-сжатых стальных колонн
В стальных колоннах выражены все три элемента: оголовок, стержень и база.
Стержни колонн передают нагрузку от оголовка на базу. Стержни центрально-сжатых колонн должны проектироваться исходя из принципа равноустойчивости, т.е. их гибкости относительно главных осей сечения должны быть равны.
Выполнение стержня колонны из прокатных широкополочных двутавров или из сварных двутавров не отвечает принципу равноустойчивости, но дает пригодное для колонн сечение.
Оголовки центрально-сжатых колонн. Оголовок является верхней частью колонны, он служит для восприятия нагрузок от вышележащих конструкций и передачи их на стержень. В связи с этим оголовки проектируются с учетом конструкции опирающихся на них балок или ферм(при этом также учитываются особенности их крепления), передачи нагрузок и с учетом сечения стержня колонны.
В сплошных колоннах опорный лист оголовка усиливают ребрами жесткости, которые препятствуют изгибу опорного листа и одновременно способствуют включению в работу всего расчетного сечения колонны. Длина ребер жесткости принимается из учета восприятия прикрепляющими их угловыми сварными швами всего приходящегося на колонну усилия.
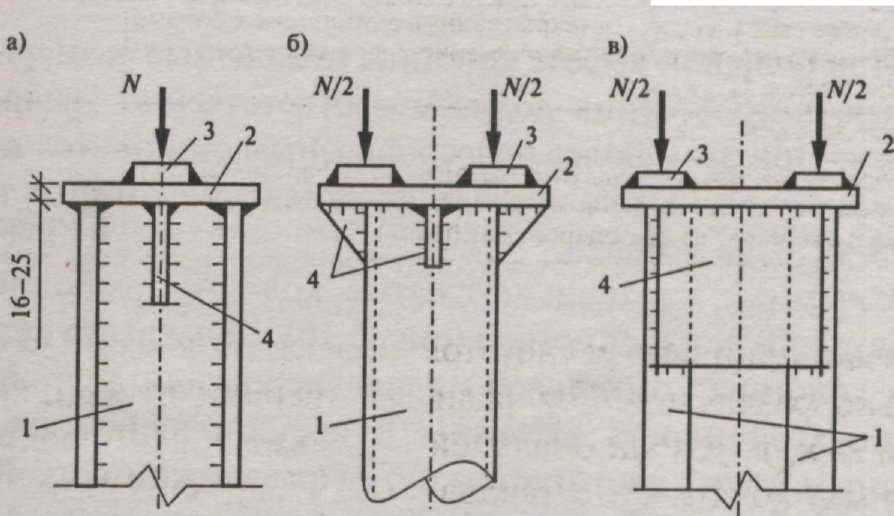
Оголовки стальных колонн с различным сечением стержней:
а) сечение стержня колонны — двутавр; б) труба; в) четыре уголка; 1 — стержень колонны; 2 — опорная плита; 3 — центрирующая пластинка; 4 — ребро жесткости.
Базы центрально-сжатых стальных колонн. База колонны предназначена для распределения нагрузки и передачи ее на фундамент. Если нагрузку не распределить, то такая колонна раздавит бетон фундамента, так как прочности стали и бетона различны и относительно небольшая площадь сечения стального стержня будет передавать значительные напряжения на бетон. База также обеспечивает крепление колонны к фундаменту.
В простейшем случае база центрально-сжатой колонны состоит из опорной плиты, к которой приварен стержень колонны. Колонна передает давление на фундамент через опорную плиту. В простейших колоннах толщина опорной плиты в этом случае может приниматься без расчета в пределах 20—60 мм.
4. Понятие о расчете сквозных центрально-сжатых колонн.
При большой высоте колонны габаритные размеры ее поперечного сечения должны соответственно увеличиваться. Целесообразно применение сквозных колонн, на изготовление которых тратится меньше металла.
Сквозные центрально-сжатые колонны выполняют из двух или четырех ветвей .Сквозные колонны компонуют из швеллеров или двутавров. Равноустойчивость колонны в обеих плоскостях (по главным осям) достигается путем раздвижки ветвей на необходимые расстояния. Колонны с соединительными планками более просты в изготовлении и применяются при расстоянии между ветвями до 0,8 м. При больших размерах сечения применяют соединительные решетки из уголков.

а) решетка из уголков; 6) соединение ветвей планками; в) сечения сквозных центрально-сжатых колонн; 1 - ветвь колонны; 2 - соединительная решетка.
Расчет внецентренно - сжатых элементов
Расчет на прочность внецентренно-сжатых, сжато-изгибаемых, внецентренно-растянутых и растянуто-изгибаемых элементов из стали с пределом текучести до 530 МПа (5400 кгс/кв.см), не подвергающихся непосредственному воздействию динамических нагрузок, при и 0,1 следует выполнять по формуле
где и - абсолютные значения соответственно продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании;
а) для сплошностенчатых стержней по табл. 74 СНиII-23-81*в зависимости от условной гибкости и приведенного относительного эксцентриситета определяемого по формуле
- относительный эксцентриситет (здесь - эксцентриситет; - момент сопротивления сечения для наиболее сжатого волокна);
б) для сквозных стержней с решетками или планками, расположенными в плоскостях, параллельных плоскости изгиба, по табл. 75 СНиII-23-81*.в зависимости от условной приведенной гибкости ( по табл. 7 СНиП II-23-81*.) и относительного эксцентриситета определяемого по формуле
При вычислении эксцентриситета значения и следует принимать согласно требованиям п. 5.29 СНиП II-23-81*.
Расчет на устойчивость не требуется для сплошностенчатых стержней при 20 и для сквозных стержней при 20, в этих случаях расчет следует выполнять как для изгибаемых элементов.
где и - коэффициенты, принимаемые по табл. 10 СНиП II-23-81*.
Контрольные вопросы
1. Как производится расчет центрально-сжатых.
2. Приведите расчет общей устойчивости центрально-сжатых элементов (понятие плоскости наименьшей жесткости).
3. Какова последовательность расчета центрально-сжатых элементов.
4. Как выполняется расчет внецентренно-сжатых элементов.
5. Приведите расчет прочности изгибаемых элементов.
6. Как учитываются пластические деформации при изгибе?
7. Как определяется общая устойчивость балки при изгибе?
8. Как рассчитывают деформации при изгибе?
Соединения в металлических конструкциях
В металлических конструкциях используют следующие виды соединений: сварные, болтовые, заклепочные и клееболтовые.
Сварные соединения
Сварка в строительстве
Особая роль в развитии и совершенствовании сварочных процессов и оборудования «надлежит отечественным ученым. Еще в 1802 г. академик В.В.Петров впервые зажег электрическую дугу и доказал возможность использования ее для плавки металла.
Практическое применение электрической дуги для сварки осуществил русский инженер Н. Н. Бернадос в 1882 г.: для сварки он использовал угольный электрод, разработал способы электрической контактной сварки, сварки в струе газа, а также автоматы для дуговой сварки.
В 1888 году инженер Н.Г. Славянов предложил способ дуговой сварки металлическим электродом (который применяется и сейчас ) и впервые ввел в практику дуговую сварку под слоем флюса (флюс - сыпучее вещество, под слоем которого горит дуга, он препятствует возникновению воздуха к расплавленном металлу и легирует металл шва).
В 1940 году под руководством академика Е.О. Патона был разработан новый высокопроизводительный способ автоматической дуговой сварки под слоем флюса, применяемый и до настоящего времени. Большая работа по изучению и развитию автоматической сварки под слоем флюса и нового способа - электрошлаковой сварки - производится институтом - электросварки им. Е.О. Патона, где впервые была создана теория сварки, разработаны флюсы и современные сварочные аппараты. В настоящее время этот институт проводит большую работу по усовершенствованию и повышению уровня методов сварки.
Сваркой называется процесс получения неразъемных соединений за счет установления межатомных связей между свариваемыми частями при местном
или общем нагреве или пластическом деформировании. При обычной температуре атомы металлов и сплавов прочно закреплены в узлах кристаллической решетки, поэтому диффузия их незначительна, Сварка в холодном состоянии требует больших усилий (давления), поэтому таким способом сваривают высокопластнчные материалы (медь, алюминий и др.).
В строительстве используют следующие виды сварки:
а) дуговая открытой дугой, дуговая под слоем флюса и в защитном газе, электрошлаковая, газовая,
в) холодная, ультразвуковая.
Преимущества электросварки:
1. Экономия стали за счет отказа то дополнительных элементов.
2. Сварные конструкции позволяют использовать полностью сечения элемента вработе.
3. Возможность производить непроницаемые для жидкостей и газов конструкции,
4. Возможность изготавливать конструкции любой формы
Недостатки электросварки:
1. Дня электросварки необходимы высококвалифицированные исполнители.
2. Возникают большие сварочные напряжения и деформации.
3. Сварка при низких температурах требует особой инженерной подготовки (предварительный подогрев), устройство тепляков и др.
4. Сварные соединения чувствительны к динамическим нагрузкам.
5. При сварке высокоуглеродистых сталей возможны трещины, необходимы дополнительные мероприятия.
6. Зона сварных швов более чувствительна к агрессивной среде.
Виды сварки
Ручная электросварка. Схема ручной электросварки и схема строения электрической показана на рис.5.1.
Качество и производительность такой сварки во многом зависят от квалификации сварщика, от условий, в которых она выполняется. При ручной сварке, применяемой чаще при монтаже конструкций, сила тока 300. 400А. Для сварки толстых элементов (более 6 мм) сварной шов выполняется за несколько проходов. Начало и конец сварки - места возможных дефектов.
ёсоздания продольной сжимающей силы применяют гидравлические или пневматические системы, для получения плотных соединений вместо электродов ставят ролики (колесики), т.е. получается шовная сварка.
Газовая сварка - применяется для сварки тонкого металла толщиной до 2. 3 мм (резервуаров, коробов). При толщине металлов до 2 мм сварку можно выполнять без присадочного металла - проволоки (для этого необходимо отогнуть металл), при толщине металлов более 2 мм необходим присадочный металл. Газовая сварка осуществляется горелкой, к которой подходят 2 шланга. По одному шлангу поступает кислород (баллон синего цвета), по другому - горючий газ (чаще всего ацетилен), поставляемый в баллонах, часто используют ацетиленовые генераторы, работающие на карбиде кальция. Все генераторы должны иметь водяной затвор (приспособление, предотвращающее возгорание ацетилена в емкости генератора).
Основные расчетные положения внецентренно сжатых элементов
Внецентренно сжатые элементы – элементы, в которых расчетные продольные сжимающие силы N действуют с эксцентриситетом продольного усилия е0 по отношению к вертикальной оси элемента или на которые одновременно действуют осевая продольная сжимающая сила N и изгибающий момент М.
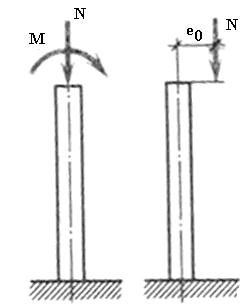
Рис. 12.3. Внецентренно сжатая колонна с начальным эксцентриситетом е0
Совокупность осевой продольной сжимающей силы N и изгибающего момента М можно заменить силой N, действующей с начальным эксцентриситетом .
Начальный эксцентриситет в любом случае принимают не менее случайного коэффициента.
Для элементов статически определимых систем проектный эксцентриситет е0 принимают не менее суммы начального и случайного эксцентриситета, т.е. .
Для элементов статически неопределимых систем проектный эксцентриситет е0 принимают не менее еа, т.е.
В соответствии с характером силового воздействия профиль внецентренно сжатых элементов принимается обычно развитым в плоскости действия момента и может быть прямоугольным, тавровым, двутавровым, коробчатым, кольцевыми т.д.
При гибкости элементов по п.3.3 СНиП 2.03.01-84* «Бетонные и железобетонные конструкции» необходимо учитывать влияние на их несущую способность прогибов в плоскости эксцентриситета продольного усилия и в нормальной к ней плоскости путем умножения значений е0 на коэффициент (см. п. 3.6).
В случае расчета из плоскости эксцентриситета продольного усилия значение е0 принимается равным значению случайного эксцентриситета еа.
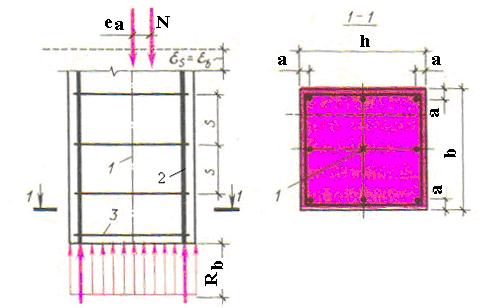
Рис. 12.4. Расчетная схема внецентренно сжатого элемента
при случайном эксцентриситете еа
1 – геометрическая ось элемента;
2 – продольная арматура;
При нагружении внецентренно сжатых элементов до предела их несущей способности (стадия III) в зависимости от величины эксцентриситета наблюдаются 2 случая разрушения:
случай 1 – случай больших эксцентриситетов (рис.12.5);
случай 2 – случай малых эксцентриситетов (рис.12.6).
Случай 1. Напряженное состояние (как и разрушение) близко к напряженному состоянию изгибаемых элементов по случаю 1. В стадии II НДС в растянутой зоне образуются нормальные трещины, а в стадии III – наступает плавное разрушение элементов. При этом напряжения в растянутой и сжатой арматуре и в бетоне сжатой зоны сечения достигают своих предельных значений: , т.е. разрушение происходит при одновременном исчерпании несущей способности растянутой арматуры и бетона и арматуры сжатой зоны сечения. При этом элементы следует проектировать, чтобы соблюдалось условие (), иначе арматура будет находиться за пределами бетона сжатой зоны, и ее прочность не будет использована. Если в расчетных уравнениях принимают .
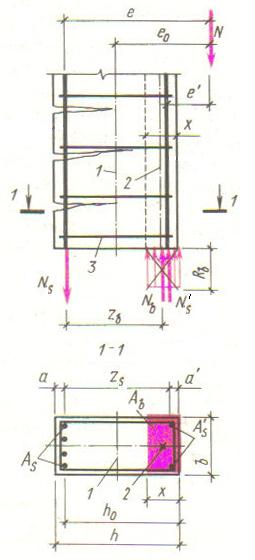
Рис. 12.5. Расчетная схема внецентренно сжатого элемента (случай 1)
1 – геометрическая ось элемента; 2 – центр тяжести бетона сжатой зоны; 3 – хомуты
Условие несущей способности элемента:
При расчете внецентренно сжатых элементов по случаю 1 возможно применение таблиц:
Таким образом, расчет при помощи таблиц внецентренно сжатых элементов аналогичен расчету при помощи таблиц изгибаемых элементов с двойной арматурой.
Случай 2. Этот случай объединяет 2 варианта наряженного состояния: когда все сечение сжато или когда часть сечения слабо растянута. В обоих вариантах разрушение элемента наступает вследствие исчерпания несущей способности бетона сжатой зоны и сжатой арматуры. При этом прочность растянутой арматуры недоиспользуется, напряжения в ней остаются низкими. В целях упрощения расчетов действительные эпюры сжимающих напряжений заменяют прямоугольной эпюрой с ординатой . Напряжения в растянутой арматуре равны , в сжатой арматуре – .
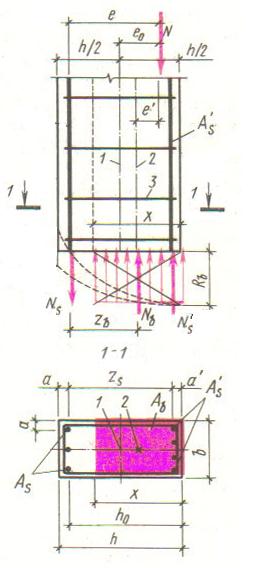
Рис. 12.6. Расчетная схема внецентренно сжатого элемента (случай 2)
Напряжения в сжатой арматуре получают из условия, что в стадии разрушения деформации бетона и арматуры, благодаря их сцеплению, одинаковы:
Отсюда предельные сжимающие напряжения в продольной арматуре :
По СНиП 2.03.01-84* «Бетонные и железобетонные конструкции» определяют по эмпирической зависимости:
, где определяют по п.3.12*.
По этой формуле находят для классов арматуры A-I (А240), A-II (А300), A-III (А400) и при бетоне класса В30 и ниже. Для других классов арматуры и класса бетона выше В30 определяют по формулам (67), (68) СНиП 2.03.01-84*.
Напряжение принимают со своим знаком; оно должно находиться в следующих пределах .
По СП 52 –101-2003 расчет по случаю1 ведется по формуле (6.21) п.6.2.15; расчет по случаю 2 ведется по формуле (6.22) п.6.2.15.
Читайте также:
