В процессе закручивания длина стального стержня

Обновлено: 24.04.2024

Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор — крутящий момент М_z. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил — касательные напряжения и ) М_z связывает вытекающее из его определения уравнение равновесия статики (рис. 24)

Условимся считать M_z положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки. Это правило проиллюстрировано на рис. 25 и в указанном соотношении, где крутящий момент М_z принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог.

Рис.24. Связь крутящего момента с касательными напряжениями

Рис.25. Иллюстрация положительного и отрицательного крутящего момента

Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 26) позволяет сформулировать следующие постудаты теории кручения этого стержня:

1. поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);

2. расстояния между поперечными сечениями не изменяются, следовательно ;

3. контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Оz. Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и ;

4. материал стержня подчиняется закону Гука. Учитывая, что , из обобщенного закона Гука в форме получаем. Это означает, что в поперечных сечениях, стержня возникают лишь касательные напряжения , а вследствие закона парности касательных напряжений, равные им напряжения действуют и в сопряженных продольных сечениях. Следовательно напряженное состояние стержня — чистый сдвиг.

Рис.26. Иллюстрация кручения: а) исходное и б) деформированное состояния

Выведем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения. Как видно, поворот правого торцевого сечения относительно неподвижного левого на угол (назовем его углом закручивания стержня) вызывает поворот продольных волокон на угол (угол сдвига), поскольку на величину искажаются углы ортогональной сетки продольных и поперечных рисок модели.

Двумя смежными сечениями вырежем элемент стержня длиной dz и, поскольку нас интересуют деформации элемента, левое сечение его будем считать неподвижным (рис. 27). При повороте правого сечения на угол в соответствии с гипотезой о недеформируемости радиусов, правый конец волокна АВ (отстоящий от оси элемента на величину полярного радиуса ) будет перемещаться по дуге BB₁, вызывая поворот волокна на угол сдвига

Обратим внимание на то, что в соответствии с рис. 5 и рис. 6, а сдвиг и связанное с ним касательное напряжение перпендикулярны радиусу . Определим , воспользовавшись законом Гука для чистого сдвига

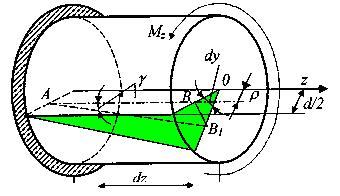
Рис.27. Расчетная модель определения касательных напряжений

а) ортогональность и
Рис.28. Распределение касательных напряжений при кручении:

Здесь — погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 28, a)

Подставляя (1) в (2) и учитывая, что

где J_p—; полярный момент инерции поперечного сечения (для круга с диаметром d ), получаем

Подставляя выражение (3) в (1), получаем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения

Как видно из (4), сдвиги и касательные напряжения пропорциональны расстояний от оси стержня. Обратим внимание на структурные аналогии формул для нормальных напряжений чистого изгиба и касательных напряжений кручения.

Мерой деформации стержня при кручении является погонный угол закручивания стержня, определяемый по (3). Поскольку величина GJ_p стоит в знаменателе формулы и при заданной нагрузке (M_z через нее выражается) тем меньше, чем больше GJ_p, последнюю называют жесткостью поперечного сечения при кручении.

Пользуясь (3) для определения угла закручивания элемента длиной dz

найдем полный угол закручивания стержня длиной l

В случае, если по длине стержня М_z и GJ_p постоянны, получаем

когда эти величины кусочно-постоянны, то:

Отметим, что полученные формулы по структуре аналогичны формулам для деформаций при растяжении стержня.

Наибольшие касательные напряжения возникают у внешней поверхности стержня, т. е. при

где W_р — момент сопротивления при кручении или полярный момент сопротивления

Полярный момент сопротивления, стоящий в знаменателе для максимальных касательных напряжений, очевидно, является геометрической характеристикой сечения, а условие прочности стержня при кручении принимает вид

где — допускаемое напряжение на кручение.

Как показали эксперименты и точное решение этой задачи в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения (рис. 7). Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d

где , а момент сопротивления определяется по формуле

Учитывая линейный характер изменения касательных напряжений по радиусу (рис. 7) и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.

Как отмечено ранее, напряженное состояние при кручении стержня — чистый сдвиг, являющийся частным случаем плоского напряженного состояния. На площадках, совпадающих с плоскостью поперечного сечения и на парных им площадках продольных сечений возникают экстремальные касательные напряжения max-min , а главные напряжения действуют на площадках, наклоненных.коси стержня под углами ; главное напряжение .

Особенности напряженного состояния при кручении нашли отражение в характере разрушения стержней. Так, разрушение стержня из дерева, плохо работающего на скалывание вдоль волокон, происходит от продольных трещин (рис. 29, a). Разрушение стержня из хрупкого металла (например, чугуна) происходит по винтовой линии, наклоненной к образующим под углом 45 o , т. е. по траектории главного напряжения (рис. 29,б).

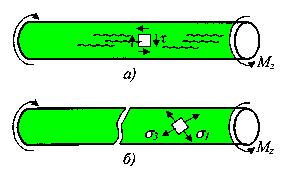
Рис.29. Распределение исходных касательных и главных напряжений: а) разрушение дерева, б) разрушение чугуна

Напряжения и деформации при кручении стержней кругового поперечного сечения

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Кручение

Внутренний крутящий момент в сечении вала М_к (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.

где М_i – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.

Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:

где - это полярные моменты инерции для сплошного и кольцевого сечений соответственно, ρ – координата произвольной точки сечения, D, d – наружний и внутренний диаметры сечения.

Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρ_max

Условие прочности по допускаемым напряжениям

где — это допускаемое касательное напряжение.

Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом

где G – модуль сдвига

Относительный угол закручивания (рад/м) для силового участка

Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде

Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.

В характерных точках сечения

угол закручивания на силовом участке вала

где α, η, β – коэффициенты, зависящие от отношения a/b (или h/b - отношение большей стороны прямоугольника к меньшей)

Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.

Касательные напряжения в характерных точках сечения

Кручение бруса тонкостенного замкнутого круглого сечения

Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:

Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:

Угол закручивания

Кручение пустотелых валов круглого сечения

Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.

Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:

Кручение бруса прямоугольного сечения

Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).

Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:

Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,

Iк=β∙h∙b3 – момент инерции при кручении.

В этих формулах: b – меньшая из сторон прямоугольника,

h – большая сторона,

α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).

Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:

Сдвиг, кручение стержней круглого сечения

5. Определение потенциальной энергии деформации тела.

Если на гранях элемента действуют только касательные напряжения, то такой вид напряженного состояния называется чистым сдвигом. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига.

Примером тела, во всех точках которого имеет место чистый сдвиг, является скручиваемый стержень круглого сечения.

Кроме расчетов на прочность при чистом сдвиге на практике часто производят расчеты на прочность по касательным напряжениям независимо от того, по каким площадкам они действуют: по площадкам чистого сдвига или по любым другим площадкам.

Такие расчеты называются расчетами на сдвиг (срез), а для дерева и бетона применяется также термин – скалывание.

Примером соединений, рассчитываемых на срез, являются заклепочные, болтовые и сварные соединения. Как показывает практика, расчеты на срез являются вполне надежными.

Напряженное состояние при чистом сдвиге

При чистом сдвиге главные напряжения получаются равными по значению и противоположные по знаку: , т.е. одно главное напряжение - растягивающее, другое – сжимающее.

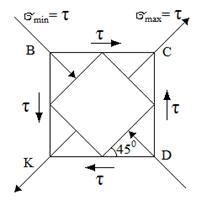Главные площадки наклонены под углом 45 0 к направлению площадок чистого сдвига

Рассмотрим теперь деформацию при сдвиге

Элемент КВСД прямоугольный до деформации после деформации (сдвига) примет вид КВ’С’Д’ (грань КД считается закрепленной). Угол - называется угловой деформацией или углом сдвига

Опыты показывают, что для многих материалов до известных пределов нагружения между напряжениями и деформациями при сдвиге имеет место линейная зависимость: , которая выражает закон Гука при сдвиге, где - модуль сдвига (модуль упругости второго рода, который характеризует способность материала сопротивляться деформации сдвига).

Линейная зависимость между и справедлива до тех пор, пока касательные напряжения не превысят предела пропорциональности при сдвиге.

При чистом сдвиге объемная деформация , т.к. , , . Из свойства взаимности касательных напряжений легко установить свойство взаимности угловых деформаций.

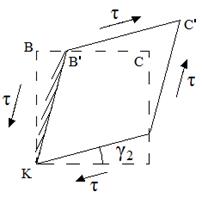Действительно, если закрепить грань КД (см. предыд. рис.), то получим угол сдвига: Закрепив теперь грань КВ’, получим для : , т.к. правые части равны, то равны и левые, т.е.

Следовательно, угловые деформации двух взаимно перпендикулярных площадок равны по значению и противоположны по знаку (свойство взаимности угловых деформаций).

Таким образом, картина перемещения элемента 1234 в результате линейных и угловых деформаций имеет вид:

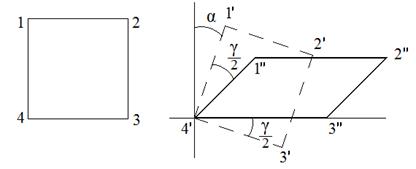
Можно сначала представить элемент 1234, как абсолютно жесткий. Он перемещается в положение 1’2’3’4’ поворачиваясь на угол .

Затем, в результате линейных деформаций происходит удлинение сторон 12 и 34 и укорочение сторон 14 и 23.

В результате угловых деформаций происходит поворот сторон 1’4’ и 4’3’ на равные по величине и противоположные по знаку углы , так что окончательно элемент 1234 будет занимать положение 4’1’’2’’3’’.

Потенциальная энергия при сдвиге.

Зависимость между тремя упругими постоянными

Вычислим потенциальную энергию при сдвиге.

Для простоты предположим, что грань КД элемента неподвижна.

Тогда, при смещении верхней грани сила (где - толщина элемента) совершит работу на перемещение .

Следовательно, потенциальная энергия деформации, накопленная в элементе:

Удельная потенциальная энергия:

Выразив через по закону Гука: , где - модуль сдвига

Множитель принят потому, что сила прямо пропорциональна смещению.

С другой стороны, потенциальная энергия может быть выражена через главные нормальные напряжения.

Для плоского напряженного состояния, каким является чистый сдвиг, принимая , получим:

Но главные напряжения при сдвиге равны и , следовательно:

т.к. энергия не должна зависеть от ориентировки граней элемента, то приравнивая правые части выражений, получим:

Отсюда найдем зависимость между модулем сдвига и модулем упругости первого рода :

Для стали модуль сдвига:

Практические расчеты на сдвиг (срез) заклепочных и сварных соединений подробно рассматриваются в курсах деталей машин и стальных конструкций.

Условие прочности заклепок на срез

- сила , действующая на соединение

Из этой формулы можно определить необходимое число односрезных заклепок: .

При двухсрезном или многосрезном заклепочном соединении вместо в формулу подставляют общее число срезов заклепок, расположенных по одну сторону стыка.

Односрезное соединение - если разрушение каждой заклепки происходит по одной плоскости среза.

Двухсрезное соединение - если разрушение каждой заклепки происходит по двум и более плоскостям.

Отверстия в склёпываемых листах имеет диаметр на 0,5-10 мм больше диаметра ещё не поставленной задачи.

В расчетные формулы входит диаметр отверстия, т.к. в выполненном соединении заклепка практически полностью заполняет отверстие.

Допускаемые касательные напряжения обычно устанавливают опытным путем для выявления влияния на прочность соединения неравномерности в распределении напряжений, влияние сил трения, зазоров.

При расчете заклепок принимают: , где - допускаемое напряжение на растяжение.

Кроме расчета на срез заклепочные соединения также рассчитывают на смятие. Проверяют напряжения смятия по площади соприкосновения соединяемых листов и заклепок. Площадь смятия одной заклепки:

( - толщина соединяемых листов).

Напряжения смятия считают равномерно распределенными по площади смятия и условие прочности на смятие имеет вид: , где -допускаемое напряжение на смятие.

Отсюда можно выразить определение необходимого числа заклепок по условию прочности на смятие: .

Кручение стержней круглого сечения

Кручением называют вид деформации бруса, при котором в его поперечных сечениях возникает один внутренний силовой фактор – крутящий момент .

Кручение бруса вызывают скручивающие (вращающие) моменты, действующие в параллельных сечениях. Обычно эти скручивающие моменты возникают под действием внешних моментов. Внешние моменты передаются на вал, как правило, в метах посадки на него шкивов, зубчатых колес и т.д.

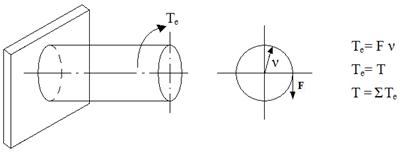
Однако и поперечная нагрузка, смещенная относительно оси стержня, вызывает крутящие моменты, но в нашем случае в поперечных сечениях, наряду с крутящими моментами, возникают и другие внутренние усилия – поперечные силы и изгибающие моменты.

Брус, нагруженный вращающимися моментами, обычно называют валом.

При равномерном вращении вала сумма вращающих моментов, действующих на вал =0.

При известных: передаваемой мощности и угловой скорости вращающий момент можно определить по формуле:

Если известна частота вращения вала , то его угловая скорость равна: , а вращающий момент .

В сопротивлении материалов реальный объект заменяют расчетной схемой, отбрасывая факторы, которые, не влияя заметно на результат, усложняют расчет.

Участки вала между сечениями, в которых приложены внешние моменты, скручиваются.

Крутящий момент в любом сечении вала определяется методом сечений.

Мысленно рассекаем вал плоскостью. Отбрасываем одну часть вала, заменив действие отброшенной части на оставленную моментом и определяем его значение из условия прочности.

Крутящий момент в сечении вала численно равен алгебраической сумме внешних (скручивающих) моментов, расположенных по одну сторону от сечения.

Если на вал действуют несколько вращающих моментов, то для определения опасного сечения или участка вала строят эпюры крутящих моментов аналогично эпюрам продольных сил.

Условно, крутящий момент считают положительным (при построении эпюр ) если, глядя на сечение, мы видим крутящий момент, направленный по часовой стрелке.

Т.к. по условию равновесия крутящий момент уравновешивает внешние моменты, приложенные к оставленной части вала, то его знак противоположен знаку внешних моментов.

Определение напряжений в стержнях круглого сечения

Крутящие моменты представляют лишь равнодействующие внутренних сил.

Фактически в поперечном сечении скручиваемого стержня действуют непрерывно распределенные внутренние касательные напряжения.

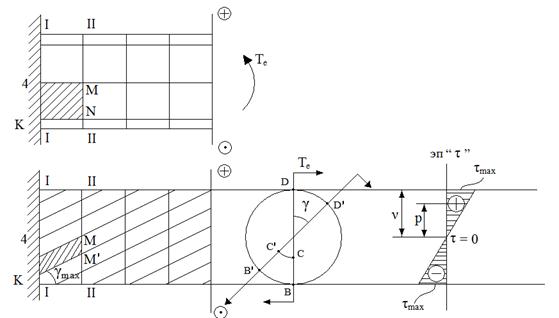
Если на поверхность стержня круглого сечения нанести прямоугольную сетку, то после деформации окажется:

1. Прямоугольная сетка, превратится в сетку, состоящую из параллелограммов. Это говорит о наличии касательных напряжений в поперечных сечениях бруса. А по закону парности касательных напряжений – и в продольных его сечениях.

2. Расстояние между окружностями, например, между I и II не изменятся. Не изменятся и длина стержня и его диаметр.

Согласно гипотезе плоских и жестких сечений каждое поперечное

сечение поворачивается в своей плоскости на некоторый угол как жесткое целое. На основании этой гипотезы можно считать, что радиусы всех поперечных сечений будут поворачиваться (на разные углы), оставаясь прямолинейными.

На основании этого можно принять, что при кручении в поперечных сечениях стержня действуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг.

Формулы, полученные на основе этого допущения, подтверждаются опытами.

Точка Д переместится по дуге ДД’, а точка С по дуге СС’,

Для установления закона распределения касательных напряжений по поперечному сечению скручиваемого стержня рассмотрим более детально деформации стержня.

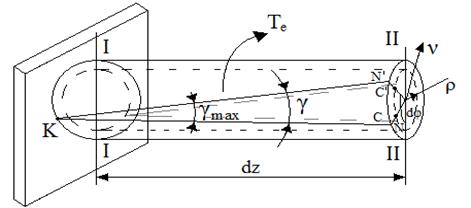
На этой схеме более детально изображена сторона KN элемента KLMN.

Угол сдвига для элемента KLMN, лежащего на поверхности стержня, равен отношению отрезка NN’ к длине элемента .

Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса и повторяя те же рассуждения, получим угол сдвига для элемента, от стоящего на расстоянии до оси стержня:

На основании закона Гука при сдвиге имеем: .

Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.

В центре тяжести круглого сечения касательные напряжения =0.

Наибольшие касательные напряжения будут в точках сечения, расположенных у поверхности стержня.

Зная закон распределения касательных напряжений (можно определить их из условия прочности), что крутящий момент в сечении представляет собой равнодействующий момент касательных напряжений в сечении:

Под интегралом – элементарный крутящий момент внутренних сил, действующих на площадке . Подставляя в формулу значение напряжений, получим: .

Выражение под интегралом во втором случае - полярный момент инерции, получим:

- формула для определения касательных напряжений при кручении.

Наибольшее касательное напряжение возникает у контура сечения:

- определение диаметра вала при кручении.

Геометрическая характеристика называется полярным моментом инерции или моментом сопротивления при кручении.

Для круглого сплошного сечения:

Условие прочности при кручении

Условие статической прочности вала при кручении имеет вид:

Кроме проверки на прочность по этой формуле можно также подбирать диаметр вала или определять допускаемый крутящий момент при известных остальных величинах: .

Опыты показывают, что хрупкие материалы, например, чугун, при кручении разрушается по плоскости (точнее говоря, по винтовой поверхности), наклоненной к оси вала под углом , т.е. по тем плоскостям, где действуют наибольшие растягивающие напряжения.

Чистый сдвиг – когда при кручении во всех точках стержня, кроме точек его оси (в которых вообще не возникает напряжений) имеется двухосное напряженное состояние.

Напряженное состояние называется неоднородным, если при кручении материал у поверхности стержня напряжен сильнее, чем материал, расположенный ближе к осям стержня.

Напряженное состояние называется однородным, если во всех точках возникают одинаковые напряжения.

Деформации и перемещения при кручении валов.

Для вычисления деформаций вала при кручении воспользуемся формулой

Деформация вала на длине (взаимный угол поворота сечений) равна:

Аналогично, для вала длиной , получим:

- определение углов закручивания.

Угол закручивания, приходящийся на единицу длины, называется относительным углом закручивания. Он равен

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого, т.е.

- условие жесткости вала при кручении. Допускаемый относительный угол закручивания в радианах на единицу длины вала.

В большинстве случаев допускаемый относительный угол закручивания задают в градусах на 1 м длины, тогда взамен этой формулы получим:

Угол выбирают в зависимости от назначения вала и его размеров. Для валов средних размеров в «Справочнике машиностроителя» рекомендуется принимать допускаемый угол закручивания равным 0,5 0 на

Определение потенциальной энергии деформации вала

При кручении внешние моменты совершают работу вследствие поворота сечений, к которым они приложены. Эта работа расходуется на создание запаса потенциальной энергии деформации, численно равной работе внутренних сил.

Аналогично тому, что было сделано при растяжении, можно доказать, что работа статически приложенного внешнего скручивающего момента равна половине произведения конечного значения момента на окончательный угол закручивания: .

Элементарная работа внутренних сил, отрицательная по знаку, и численно равная ей потенциальная энергия при кручении равна:

- угол закручивания элемента длиной

Если крутящий момент и жесткость стержня не меняются по длине, то имеем: .

Гипотезы теории кручения валов круглого сечения

1. Сечения, плоские до деформации, остаются плоскими и после деформации, поворачиваясь относительно друг друга на некоторый угол (гипотеза плоских сечений).

2. Расстояния между поперечными сечениями в процессе деформации не изменяются, т.е. длина вала остается постоянной.

3. Радиусы поперечных сечений при деформации вала не искривляются.

Эти гипотезы подтверждаются не только экспериментальными

исследованиями, но также точным решением задачи методами теории упругости

Условия и порядок выполнения

1. Стальной вал круглого сплошного поперечного сечения нагружен внешними скручивающими моментами в соответствии с заданной схемой.

Требуется построить эпюру внутренних крутящих моментов и из условия прочности определить диаметр вала. Полученный из расчета диаметр вала округлить до ближайшего целого числа соответственно: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100.

2. Для принятого диаметра вала построить эпюру углов закручивания по- перечных сечений относительно крайнего левого сечения. Определить также наибольший относительный угол закручивания (на 1 пог. м.). Модуль упругости при кручении для стали принять равным 8∙10 4 МПа.

3. Исходные данные для решения задачи (вариант) берутся из табл. 3. Нумерация моментов для всех задач постоянна, как показано на первых рисунках.

Таблица 3

Исходные данные к заданию 3

Вариант	Длины участков, м	Внешние скручивающие моменты, кНм	Допускаемое касательное напряжение, [τ],МПа
а	в	с	Т₁	Т₂	Т₃	Т₄
1,1	1,3	0,8	1,3	1,5	1,8	1,0
1,2	1,4	0,9	1,4	1,6	1,9	1,1
1,3	1,5	1,0	1,5	1,7	2,0	1,2
1,4	1,6	1,1	1,6	1,8	2,1	1,3
1,5	1,7	1,2	1,7	1,9	2,2	1,4
1,6	1,8	1,3	1,8	2,0	2,3	1,5
1,7	1,9	1,4	1,9	2,1	2,4	1,6
1,8	2,0	1,5	2,0	2,2	2,5	1,7
1,9	2,1	1,6	2,1	2,3	2,6	1,8
2,0	2,2	1,7	2,2	2,4	2,7	1,9

Задача 5. Кручение

Задача 5 (продолжение)

Задача 5 (окончание)

Пример решения задачи 3

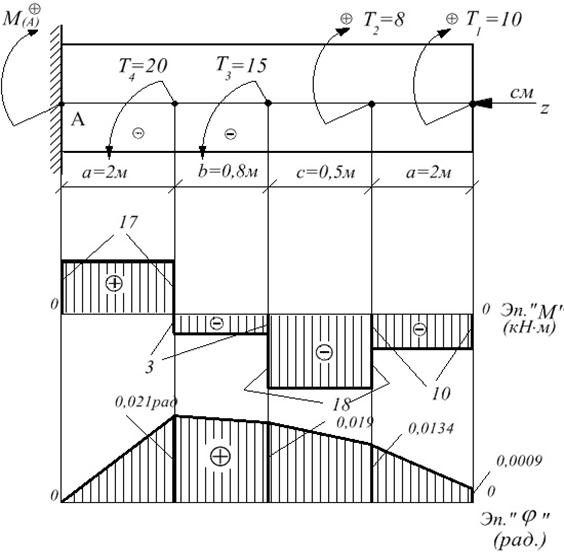1. Определение реактивного момента в жесткой заделке в т. А:

2. Определение внутренних крутящих моментов, возникающих в сечениях стержня:

Решение типовых задач по сопромату.

Пример решения задачи на кручение стержня круглого сечения

Кручение стержня круглого сечения – условие задачи

К стальному валу постоянного поперечного сечения (рис. 3.8) приложены четыре внешних скручивающих момента: кН·м; кН·м; кН·м; кН·м. Длины участков стержня: м; м, м, м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при кН/см2 и построить эпюру углов закручивания поперечных сечений стержня.

Кручение стержня круглого сечения – расчетная схема

Решение задачи кручение стержня круглого сечения

Определяем реактивный момент, возникающий в жесткой заделке

Обозначим момент в заделке и направим его, например, против хода часовой стрелки (при взгляде навстречу оси z).

Запишем уравнение равновесия вала. При этом будем пользоваться следующим правилом знаков: внешние скручивающие моменты (активные моменты, а также реактивный момент в заделке), вращающие вал против хода часовой стрелки (при взгляде на него навстречу оси z), считаем положительными.

Знак «плюс» в полученном нами выражении говорит о том, что мы угадали направление реактивного момента , возникающего в заделке.

Строим эпюру крутящих моментов

Напомним, что внутренний крутящий момент , возникающий в некотором поперечном сечении стержня, равен алгебраической сумме внешних скручивающих моментов, приложенных к любой из рассматриваемых частей стержня (то есть действующих левее или правее сделанного сечения). При этом внешний скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки (при взгляде на поперечное сечение), входит в эту алгебраическую сумму со знаком «плюс», а по ходу – со знаком «минус».

Соответственно, положительный внутренний крутящий момент, противодействующий внешним скручивающим моментам, направлен по ходу часовой стрелки (при взгляде на поперечное сечение), а отрицательный – против ее хода.

Разбиваем длину стержня на четыре участка (рис. 3.8, а). Границами участков являются те сечения, в которых приложены внешние моменты.

Делаем по одному сечению в произвольном месте каждого из четырех участков стержня.

Cечение 1 – 1. Мысленно отбросим (или закроем листком бумаги) левую часть стержня. Чтобы уравновесить скручивающий момент кН·м, в поперечном сечении стержня должен возникнуть равный ему и противоположно направленный крутящий момент . С учетом упомянутого выше правила знаков

Сечения 2 – 2 и 3 – 3:

Сечение 4 – 4. Чтобы определить крутящий момент, в сечении 4 – 4 отбросим правую часть стержня. Тогда

Легко убедиться в том, что полученный результат не изменится, если мы отбросим теперь не правую, а левую часть стержня. Получим

Для построения эпюры крутящих моментов проводим тонкой линией ось, параллельную оси стержня z (рис. 3.8, б). Вычисленные значения крутящих моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В пределах каждого из участков стержня крутящий момент постоянен, поэтому мы как бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним, что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе значение крутящего момента в соответствующем поперечном сечении стержня. Полученную эпюру обводим жирной линией.

Отметим, что в местах приложения внешних скручивающих моментов на эпюре мы получили скачкообразное изменение внутреннего крутящего момента на величину соответствующего внешнего момента.

Определяем диаметр вала из условия прочности

Условие прочности при кручении имеет вид

где – полярный момент сопротивления (момент сопротивления при кручении).

Наибольший по абсолютному значению крутящий момент возникает на втором участке вала: кН·см.

Тогда требуемый диаметр вала определяется по формуле

Округляя полученное значение до стандартного, принимаем диаметр вала равным мм.

Определяем углы закручивания поперечных сечений A, B, C, D и E и строим эпюру углов закручивания

Сначала вычисляем крутильную жесткость стержня , где G – модуль сдвига, а – полярный момент инерции. Получим

Углы закручивания на отдельных участках стержня равны:

Угол закручивания в заделки равен нулю, то есть . Тогда

Эпюра углов закручивания показана на рис. 3.8, в. Отметим, что в пределах длины каждого из участков вала угол закручивания изменяется по линейному закону.

Пример задачи на кручение "круглого" стержня для самостоятельного решения

Условие задачи на кручение "круглого" стержня

Жестко защемленный одним концом стальной стержень (модуль сдвига кН/см2) круглого поперечного сечения скручивается четырьмя моментами (рис. 3.7).

· построить эпюру крутящих моментов;

· при заданном допускаемом касательном напряжении кН/см2 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм;

Читайте также: