Тонкая структура спектральных линий водорода и щелочных металлов
Обновлено: 17.05.2024
Запишем УШ для атома водорода (единственное уравнение атомной физики, которое можно решить аналитически):
Для решения данного уравнения необходимо перейти к сферической СК, при этом УШ решается методом разделения переменных и решение имеет следующий вид:
УШ допускает два типа решений:
Энергия водорода зависит только от главного квантового числа, в то время как волновая функция определяется тремя числами
Пусть водород находится в первом состоянии.
Второй энергитический уровень водорода четырехскоростно вырожден.
Вырождение по орбитальному квантовому числу для водорода случайно, т.к. электростатическое поле протона и электрона – кулоново.
Независимость энергии от снимается.
Найдем кратность вырождения уровня энергии водорода. Любому квантовому числу значений значений кратность вырождения:
С учетом спина электрона:
В спектроскопии уровни энергии атомов обозначают:
Обобщенная формула Бальмера для спектроскопии волнового числа:
Схема уровней атома водорода.

Правила отбора для радиационных переходов являются следствием закона сохранения четности, а также закона сохранения момента импульса в дипольном приближении.
Правила отбора заключаются в следующем. При радиационных переходах возможны следующие изменения квантовых чисел.
Таким образом S уровни комбинируют только с P уровнями.
Рассмотрим волновые функции атома водорода:
Сферические функции , приРассмотрим плотность вероятности
Вероятность обнаружить электрон на расстоянии и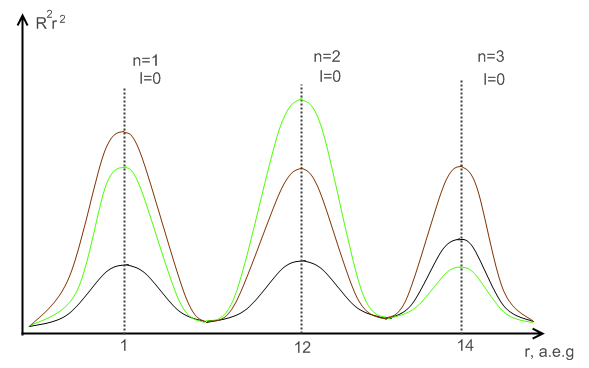

§29. Щелочные металлы.
Щелочные металлы образуют первую группу периодической системы элементов и имеют один валентный электрон на внешней оболочке. Внутренние электроны и ядро атома щелочного металла образуют прочный остов.
В случае щелочного металла электростатическое поле, как и у водорода, сферически симметрично, но уже не кулоново. Если внешний электрон находится на значительном расстоянии от остова, то он движется в поле с эффективным электрическим зарядом- поле точечного заряда
- поле диполя
Подставляя данную формулу потенциальной энергии в УШ и решая последнее, получаем спектр энергии щелочного металла:
Энергия зависит от двух квантовых чиселДля водородоподобного атома:
Для щелочных металлов:
Правила отбора для щелочных металлов.
Схема уровней атома натрия:

Основные серии щелочного металла:
Вторая побочная (резкая)
Первая побочная (диффузная)
Опытным путем было установлено, что спектральные линии щелочных металлов дублетны (двойные), что связано с тем, что во всех состояниях, кромеПод спин-орбитальным взаимодействием понимают взаимодействие магнитного орбитального момента электрона с его спиновым магнитным моментом, в результате чего появляется зависимость энергии атома от спинового квантового числа.
Т.к. в , то спин-орбитального взаимодействия в данном случае нет и уровни энергии одинарные.
§. Общая векторная модель атома.
Электроны в атоме имеют орбитальные механические моменты, которые складываются в общий или полный механический момент импульса атома:
Складывать эти вектора можно различными способами.
Первый способ.Данный способ реализуется для атомов легких элементов, при этом кулоново отталкивание электронов преобладает над спин-орбитальным взаимодействием. В результате чего каждый электрон обладает собственным орбитальным механическими моментами, которые, складываясь по раздельности, дают результирующий орбитальный и спиновый механические моменты атома.
Полный механический момент атома также по квантовым законам определяется, как сумма орбитального и спинового момента.
- полное (внутреннее) квантовое число.
Как правило,(за исключением ).
Для атомов с одним валентным электроном, спиновое квантовое числоПолный механический момент:


; – быстрые прецессии.
- медленная прецессия.
В центральном поле сохраняется только вектор и- магнитное внутреннее квантовое число.

Если внутренние оболочки атома полностью заполнены, то моменты импульсов . Т.о. в общей векторной модели атома учитываются только механические и магнитные моменты легких электронов в незаполненных оболочках.
Второй способ.Характерен для тяжелых атомов с большим количеством валентных электронов, в данном случае, спин-орбитальное взаимодействие каждого электрона преобладает над электростатическим отталкиванием электронов между собой, в результате чего у каждого из них есть полный механический момент.
Все моменты складываются в общий механический момент.
Очевидно, что как и в случае такое же, но уровни энергии при этом будут отличаться, т.к. различна природа взаимодействия. При этом величины:
полностью теряют смысл.
§. Тонкая структура спектральных термов
щелочных металлов и атома водорода.
Тонкой структурой называют расщепление энергитических уровней в результате спин-орбитального взаимодействия.
Рассмотрим атом с одним валентным электроном.
В спектроскопии для обозначения уровня энергии и соответствующего спектрального терма вводится следующая запись:
Для атома водорода уровни энергии вырождены по и уровни энергии совпадают.
Рассмотрим термы водородоподобного атома с учетом тонкой структуры:
С ростом зарядового числа увеличивается. С ростом главного квантового числа уменьшается.
§. Тонкая структура спектральных линий
щелочных металлов и атома водорода. Лэмбовский сдвиг.
Главная серия щелочных металлов.
Рассмотрим
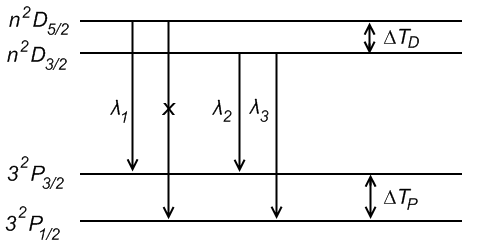
Рассмотрим спектральные линии атома водорода.

Картина, аналогичная главной серии щелочных металлов.


В 1947 году в опытах Лэмба и Резерфорда было установлено, что для атома водорода уровни , которые по теории Дирака должны совпадать, имеют различные значения энергии.

Разность между уровнями тонкой структуры водорода с одинаковыми , и разными , электрон – позитронными, протон – антипротонными и другими парами частиц и античастиц.
Точные измерения Лэмбовского сдвига показали, что закон Кулона выполняется на расстояниях вплоть до серии Бальмера состоит из семи компонент.
§. Понятие о сверхтонкой структуре спектральных линий.
Сверхтонкая структура обусловлена спин – спиновым взаимодействием. Спин – спиновое взаимодействие связано с взаимодействием магнитного спинового .
С учетом сверхтонкого расщепления, на переходы между термами различных состояний накладывается дополнительное правило отбора:
§. Применение векторной модели к атомам с двумя валентными электронами.
К атомам с двумя валентными электронами относится изоэлектронный ряд и соответствующие элементы второй группы ПСЭ:Рассмотрим гелий
Второй электрон варьирует.
Такое обозначение спектрального терма многоэлектронного атома включает в себя спектральные термы каждого из электронов и результирующий терм всего атома.
Дополнительное правило отбора для данных атомов:
§. Магнитный момент атомов.
Т.о. полный магнитный момент атома определяется суммой моментов, вычисленных с учетом правил пространственного квантования.
Пренебрегаем
Результирующий магнитный момент атома не коллинеарен результирующему механическому моменту, но его можно разложить на две составляющие:
Т.к. прецессируют относительно прецессирует относительно равна продольной составляющей
в) Магнитный момент атома может быть равен нулю даже при отличных от нуля механических моментах (диамагнетик).
Тонкая структура спектральных линий водорода и щелочных металлов
Исследование спектров щелочных металлов при помощи приборов с большой разрешающей силой показало, что каждая линия этих спектров является двойной (дублет). Так, например, характерная для натрия желтая линия (см. рис. 29.1) состоит из двух линий с длинами волн 5890 и 5896 А. То же относится и к другим линиям главной серии, а также к линиям других серий.
Структура спектра, отражающая расщепление линий на компоненты, называется тонкой структурой. Сложные линии, состоящие из нескольких компонент, получили название мультиплетов. Тонкая структура обнаруживается, кроме щелочных металлов, также и у других элементов, причем число компонент в мультиплете может быть равно двум (дублеты), трем (триплеты), четырем (квартеты), пяти (квинтеты) и т. д. В частном случае спектральные линии даже с учетом тонкой структуры могут быть одиночными (синглеты).
Расщепление спектральных линий, очевидно, обусловлено расщеплением энергетических уровней. Для объяснения расщепления уровней Гаудсмит и Уленбек выдвинули в 1925 г. гипотезу о том, что электрон обладает собственным моментом импульса , не связанным с движением электрона в пространстве.
Этот собственный момент был назван спином.
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Согласно этим представлениям электрон уподоблялся волчку или веретену. Кстати, отсюда происходит и сам термин «спин»: по-английски spin означает «верчение». Однако очень скоро пришлось отказаться от подобных модельных представлений, в частности по следующей причине. Вращающийся заряженный шарик должен обладать магнитным моментом, причем отношение магнитного момента к механическому должно иметь значение
(см. формулу (56.3) 2-го тома).
Действительно, было установлено, что электрон, наряду с собственным механическим моментом, обладает также и собственным магнитным моментом Однако ряд опытных фактов, в частности сложный эффект Зеемана, свидетельствует о том, что отношение собственных магнитного и механического моментов в два раза больше, чем для орбитальных моментов:
Таким образом, представление об электроне как о вращающемся шарике оказалось несостоятельным. Спин следует считать внутренним свойством, присущим электрону, подобно тому как ему присущи заряд и масса.
Предположение о спине электрона было подтверждено большим количеством опытных фактов и должно считаться совершенно доказанным. Оказалось также, что наличие спина и все его свойства автоматически вытекают из установленного Дираком уравнения квантовой механики, удовлетворяющего требованиям теории относительности. Таким образом, выяснилось, что спин электрона является свойством одновременно квантовым и релятивистским. Спином обладают также протоны, нейтроны, фотоны и другие элементарные частицы (кроме мезонов).
Величина собственного момента импульса электрона определяется по общим законам квантовой механики (см. формулу (24.2)) так называемым спиновым квантовым числом s, равным
Проекция спина на заданное направление может принимать едантованные значения, отличающиеся друг от друга на
Чтобы найти значение собственного магнитного момента электрона, умножим на отношение (см. (31.2)):
( - магнетон Бора; см. формулу (56.7) 2-го тома). Знак минус указывает на то, что механический и магнитный моменты электрона направлены в противоположные стороны.
Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:
(минус получается, если плюс — если
Таким образом, проекция собственного момента импульса электрона может принимать значения а собственного магнитного момента — значения . В ряд формул, в частности в выражение для энергии, входят не сами моменты, а их проекции. Поэтому принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается: в единицах ), а собственный магнитный момент равен одному магнетону Бора.
Рассмотрим теперь на примере атома натрия, как существование спина электрона может объяснить мультиплетную структуру спектра. Поскольку момент атомного остатка равен нулю, момент атома натрия равен моменту валентного электрона. Момент же электрона будет слагаться из двух моментов: орбитального обусловленного движением электрона в атоме, и спинового не связанного с движением электрона в пространстве. Результирующая этих двух моментов дает полный момент импульса валентного электрона. Сложение орбитального и спинового моментов в полный момент осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов (см. формулы (24.7) и (24.8)). Вели чина полного момента определяется квантовым числом
причем может иметь значения
где I и s — соответственно азимутальное и спиновое квантовые числа. При квантовое число имеет только одно значение; При отличном от нуля, возможны два значения> , которые соответствуют двум возможным взаимным ориентациям моментов — «параллельной» и «антипараллельной».
Теперь учтем, что с механическими моментами связаны магнитные моменты, которые взаимодействуют друг с другом подобно тому, как взаимодействуют два тока или две магнитные стрелки. Энергия этого взаимодействия (называемого спин-орбитальным взаимодействием) зависит от взаимной ориентации орбитального и собственного моментов. Следовательно, состояния с различными должны обладать различной энергией.
Таким образом, каждый терм ряда расщепляется на два, соответствующих каждый терм ряда расщепляется на термы с и т. д. Каждому терму ряда соответствует только одно значение поэтому термы ряда S не расщепляются.
Итак, каждый ряд термов, кроме S, распадается на два ряда — структура термов оказывается дублетной (двойной). Термы принято обозначать символами:
Правый нижний индекс дает значение j. Верхний левый индекс указывает мультиплетность термов. Хотя ряд S является одиночным, при символе терма также ставится 2, чтобы показать, что этот ряд принадлежит к системе термов, в целом дублетной.
С учетом тонкой структуры схема термов выглядит более сложно, о чем дают представление схемы уровней натрия (рис. 31.1) и цезия (рис. 31.2). Схему для натрия следует сравнить со схемой, изображенной на рис. 29.1. Поскольку мультиплетное расщепление термов D и F для натрия очень мало, подуровни D и F, отличающиеся значениями изображены на схеме слитно.
Для квантового числа полного момента импульса атома имеется правило отбора
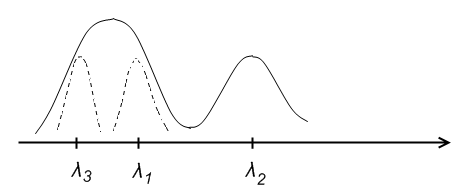
Мультиплетное расщепление у цезия значительно больше, чем у натрия. На схеме цезия видно, что тонкая структура диффузной серии состоит не из двух линий, а из трех:
Возникновение этих линий пояснено дополнительно на рис. 31.3. Изображенный пунктиром переход запрещен правилом отбора (31.7). В нижней части схемы показано, как выглядит сам мультиплет.
Толщина линий на схеме примерно соответствует интенсивности спектральных линий. Совокупность получающихся линий выглядит как дублет, у которого одна из компонент в свою очередь оказывается двойной.
Такая группа линий называется не триплетом, а сложным дублетом, так как она возникает в результате комбинации дублетных термов.
Заметим, что в связи с существованием спина электрона естественно возникает вопрос о том, что и у водородного атома уровни с должны быть двойными, а спектральные линии — дублетными.
Тонкая структура водородного спектра действительно была обнаружена экспериментально.
Обусловленное спином расщепление энергетических уровней является релятивистским эффектом. Релятивистская квантовая теория дает для расстояния между уровнями тонкой структуры водородного атома значение
Здесь — энергия ионизации водородного атома (вычисленная в предположении, что масса ядра бесконечно велика), а — безразмерная величина, называемая постоянной тонкой структуры.
Она определяется выражением
С помощью формулы (31.8) можно оценить величину мультиплетного расщепления уровней. Расстояния между уровнями, отличающимися значениями главного квантового числа, имеют величину порядка выражение имеет значение порядка . Следовательно, расстояние между уровнями тонкой структуры примерно в раз меньше, чем расстояние между основными уровнями.
Постоянная тонкой структуры принадлежит к числу фундаментальных констант природы. Ее смысл становится очевидным при переходе к так называемой естественной системе единиц, применяемой в квантовой электродинамике. В этой системе в качестве единицы массы принимается масса электрона те, в качестве единицы длины — комптоновская длина волны электрона (см. § 11), в качестве единицы энергии — энергия покоя электрона и т. д. Вычислим в этих единицах электрическую энергию взаимодействия двух электронов, находящихся на расстоянии друг от друга. Для этого нужно выражение разделить на В результате получится безразмерная величина, равная
(см. формулу (31.9)). Если бы мы заряд электрона q выражали в естественных единицах, то формула для энергии взаимодействия имела бы вид
Отсюда следует, что а представляет собой квадрат элементарного заряда, выраженного в естественных единицах.
Согласно (31.10) постоянная тонкой структуры характеризует энергию взаимодействия двух электронов. Иначе можно сказать, что а определяет, как сильно электрон связан с электромагнитным полем. По этой причине постоянную а называют константой связи электрона с электромагнитным полем.
В выражение (31.10) для а масса электрона не входит. Следовательно, а является константой связи с электромагнитным полем для любой элементарной частицы, имеющей заряд .
Атом водорода представляет собой связанное состояние положительно заряженного ядра с зарядом е и электрона с зарядом — абсолютная величина заряда электрона). Поэтому потенциал имеет вид
Мы рассмотрим задачу о движении в поле
Такой потенциал соответствует атому водорода при и водородоподобным ионам при . Оператор Шредингера в координатном представлении имеет вид
где — приведенная масса, а и М — массы электрона и ядра соответственно. Задачу будем решать в так называемой атомной системе единиц, в которой . Тогда радиальное уравнение Шредингера принимает вид
Мы будем интересоваться дискретным спектром, поэтому рассмотрим случай . Удобно обозначить . Тогда
Приведенные в предыдущем параграфе соображения о поведении решения при подсказывают, что решение удобно искать в виде
Если мы сумеем найти представимую сходящимся степенным рядом
с такую, что удовлетворяет (1), то будет обеспечено и правильное поведение при Поведение при конечно, будет зависеть от асимптотики функции при .
Подстановку (2) в уравнение (1) удобно сделать в два приема. Вводя функцию
Ищем решение этого уравнения в виде ряда (3)
Сделаем замену значка суммирования в первых двух слагаемых в квадратной скобке, тогда
Приравнивая коэффициенты при степенях , получим
По признаку Даламбера видно, что ряд сходится при всех . Оценим поведение ряда с коэффициентами, определяемыми (4) при больших . Асимптотика при конечно, определяется
коэффициентами при больших степенях, но тогда
Таким образом, для решения при получим
(Разумеется, приведенное рассуждение можно было бы сделать более точным.)
Мы видим, что решение радиального уравнения, имеющее правильное поведение при экспоненциально возрастает при Из формулы (4) видно, однако, что существуют такие значения k, что ряд будет обрываться на некотором члене. В этом случае функция окажется многочленом, а решение будет квадратично интегрируемым. Обозначим через k номер старшего коэффициента, отличного от нуля, т. е. . Из (1) видно, что это возможно, если
Из формулы получаем
Параметр k является введенным ранее радиальным квантовым числом. Мы видим, что собственные значения зависят только от . Это число называется главным квантовым числом. Вспоминая, что получаем: . Далее при заданном квантовое число I может принимать значения .
Итак, мы получили следующие результаты. Для собственных значений Е справедлива формула
а собственные функции имеют вид
где — многочлен степени , коэффициенты которого находятся по формуле (4), условия нормировки. Мы видим, что число собственных значений бесконечно и имеет точку сгущения Нетрудно определить кратность собственного значения Каждому соответствуют собственные функции , различающиеся квантовыми числами , причем .
Для кратности q получим
Кратность собственных значений для кулоновского поля оказывается большей, чем в общем случае центрального поля, имеет место дополнительное вырождение по I. Мы уже упоминали, что это «случайное» вырождение объясняется наличием более богатой, чем группы симметрии у оператора Шредингера для атома водорода.
Посмотрим теперь, какую физическую информацию дает нам решение уравнения Шредингера для атома водорода. Прежде всего мы нашли допустимые значения энергии, которые разумно привести в обычных единицах. Для этого достаточно умножить выражение (6) для на атомную единицу энергии, равную
Будем считать, что , т. е. рассмотрим атом водорода, тогда
Для энергии основного состояния атома водорода имеем
Абсолютная величина этой энергии называется потенциалом ионизации или энергией связи электрона в атоме и равна работе, которую нужно совершить, чтобы вырвать электрон из атома.
Формула (8) позволяет вычислить частоты спектральных линий атома водорода. Квантовая электродинамика подтверждает гипотезу Бора о том, что частота спектральной линии определяется по формуле
причем имеет место поглощение светового кванта, если атом переходит из состояния с меньшей энергией в состояние с большей энергией и излучение при обратном переходе.
Для частот спектральных линий имеет место формула
Эта формула называется формулой Бальмера и была открыта им чисто эмпирически задолго до создания квантовой механики.
Обратим внимание на зависимость частот от приведенной массы . В природе существует две разновидности водорода: обычный водород Н, ядром которого является протон с массой ( — масса электрона) и в небольшом количестве тяжелый водород — дейтерий D, ядро которого вдвое тяжелее протона. Используя формулу , легко сосчитать, что , т. е. приведенные массы очень близки. Тем не менее точность спектроскопических измерений (длины волн измеряют с точностью в 7—8 значащих цифр) позволяет надежно измерить отношение для соответствующих линий. Это отношение получается тоже равным 1,000272 (для некоторых линий возможно расхождение в последнем знаке). Вообще теоретически вычисленные по формуле (9) и экспериментальные значения частот совпадают с точностью в 5 значащих цифр. Имеющиеся расхождения, однако, могут быть устранены, если учесть релятивистские поправки.
Наряду с переходами между стационарными состояниями дискретного спектра возможны переходы из дискретного спектра в непрерывный и обратные переходы; физически они соответствуют
процессам ионизации и рекомбинации (захвата электрона ядром). В этих случаях наблюдается непрерывный спектр поглощения или излучения
Спектральные линии водорода на спектрограммах группируются в серии, соответствующие определенному значению в формуле (9) и . Нескольким первым сериям присвоены имена: серия Лаймана серия Бальмера серия Пашена . Линии серий Лаймана лежат в ультрафиолетовой части спектра, первые четыре линии серии Бальмера в видимой части спектра, линии серии Пашена и последующих серий в инфракрасной части спектра. К концу каждой серии линии сгущаются к так называемой границе серии, за которой начинается непрерывный спектр.
На рис. 8 горизонтальными линиями изображены энергетические уровни атома водорода, а вертикальными отрезками — возможные переходы между ними. Заштрихована область непрерывного спектра.
На рис. 9 схематично изображен вид спектральной серии, пунктиром изображена граница серии.
Важными характеристиками атомов являются вероятности переходов между состояниями. От вероятностей переходов зависят интенсивности спектральных линий. Переходы бывают спонтанные (самопроизвольные) с верхнего уровня на нижний с излучением кванта, вынужденные (под действием светового потока) и, наконец, переходы за счет столкновений с заряженными частицами. Формулы для вычисления вероятностей спонтанных и вынужденных переходов дает квантовая электродинамика, переходы за счет столкновений изучаются в квантовой теории рассеяния. Для вычисления всех этих характеристик необходимо знание волновых функций. Кроме того, знание волновых функций дает возможность судить о размерах атомов, распределении заряда в атоме и даже о форме атома.
Напомним, что есть плотность функции распределения координат. Под размером атома понимают размер той области, в которой не является пренебрежимо малой. Ясно, что размер атома — понятие условное.
Рассмотрим для примера основное состояние атома водорода . Учитывая, что по формуле (7) получим
Из условия нормировки находим постоянную С:
Легко понять, что
есть плотность функции распределения координаты . График этой функции изображен на рис. 10. Максимум достигается при — наиболее вероятное расстояние электрона от ядра. В обычных единицах см. Интересно отметить, что это число совпадает с радиусом первой боровской орбиты. Мы видим, что размеры атома водорода имеют порядок см.
Под плотностью заряда в атоме понимают величину , т. е. считают, что электрон за счет быстрого движения около ядра как бы размывается по объему атома, образуя электронное облако.
Наконец, вид функции (7) показывает, что при плотность распределения координат не является сферически симметричной. Зависимость этой плотности от углов позволяет говорить о форме атома в различных состояниях.
В этом же параграфе мы рассмотрим простую модель атомов щелочных металлов, основанную на предположении, что их оптические свойства объясняются движением валентного электрона в некотором центральном поле Потенциал можно записать в виде суммы двух слагаемых
где первое слагаемое описывает взаимодействие электрона с ядром, может быть истолкован как потенциал взаимодействия электрона с распределенным по объему атома отрицательным зарядом остальных электронов. Разумность такой модели именно для атомов щелочных металлов станет понятной только после того, как мы познакомимся со свойствами сложных атомов и таблицей Менделеева.
О потенциале мы знаем очень мало, но все же можно утверждать, что
Первое условие следует из того очевидного факта, что при удалении валентного электрона на бесконечность он оказывается в поле положительного однозарядного иона. Второе условие вытекает из непрерывности потенциала объемного распределения зарядов .
В качестве модельного потенциала мы выберем
Несмотря на то, что этот потенциал обладает правильным поведением на бесконечности, он имеет иное, чем «истинный» потенциал поведение в нуле. В то же время модельный потенциал правильно отражает тот факт, что при приближении к ядру поле становится более сильным, чем кулоновское . Мы предположим, что параметр а мал (в каком смысле, укажем ниже). Численные значения этого параметра для разных атомов щелочных металлов разумнее всего выбирать из сравнения результатов расчетов энергетических уровней с найденными экспериментально.
Радиальное уравнение для такого потенциала решается очень просто. Действительно, оно имеет вид
Введем число Г, которое удовлетворяет уравнению
и условию откуда получим . Уравнение (10) может быть переписано в виде
т. е. формально совпадает с уравнением для кулоновского поля. Все это может иметь смысл только при условии, что . В противном случае мы получим для V комплексные значения
Предположим, что тогда условие выполняется при всех . Обычно с точностью до членов порядка , т. е.
Тогда используя формулу (5) при , получим
или, вводя главное квантовое число ,
Из формулы (11) видно, что для потенциала (9) снимается кулоновское вырождение по I. Уровни энергии лежат глубже, чем уровни атома водорода и с ростом уровни сближаются. Формула (11) неплохо описывает уровни энергии атомов щелочных металлов при соответствующем значении а. Эта формула была впервые получена Ридбергом на основе анализа экспериментальных данных. Заметим, что для атомов щелочных металлов главное квантовое число, как и для водорода, принимает целые значения, но минимальное значение равно не 1, а 2 для для так как состояния с меньшим главным квантовым числом заняты электронами внутренних оболочек атома (это утверждение станет понятным после того, как мы познакомимся со строением сложных атомов).
В заключение заметим, что рассмотренная модель иллюстрирует полуэмпирический подход к решению сложных квантово-механических задач. Такой подход состоит в следующем: вместо того чтобы решать задачу в точной постановке, из физических соображений строится упрощенная модель системы. Оператор Шредингера для модельной задачи обычно зависит от параметров, найти которые теоретически так же трудно, как и решить задачу во всем объеме. Поэтому параметры находятся из сравнения результатов расчетов модельной задачи с экспериментальными данными.
Внешняя картина спектра любого щелочного металла отличается довольно большой сложностью по сравнению с водородным спектром. Сложность картины объясняется тем, что спектральные линии отдельных серий «перепутаны» между собой (рис. 254).
Рис. 254. Спектр натрия.
Несмотря на это, Ридбергу при анализе спектров щелочных металлов удалось установить, что частоты всех спектральных линий можно представить как попарные разности четырех систем термов:
Дробные величины s, р, d, f как бы характеризуют уклонение этих термов от водородных, обратно пропорциональных просто квадратам целых чисел (§ 58).
Так же как у атома водорода, каждый терм мы рассматриваем как величину, характеризующую соответствующий энергетический уровень атома щелочного металла. Таким образом, система энергетических уровней атомов щелочных металлов оказывается более сложной, чем у атома водорода. Это усложнение системы энергетических уровней, безусловно, связано с более сложной внутренней структурой атомов щелочных металлов. Действительно, в состав электронных оболочек этих атомов входит уже не один, а несколько электронов: у лития 3, натрия 11, калия 19, рубидия 37, цезия 55. Задача о движении нескольких электронов, входящих в оболочку одного атома, представляет собой частный случай так называемой проблемы многих тел, не решаемой точно ни в орбитальной модели, ни в волновой механике.
Трудность заключается в учете взаимодействия электронов между собой. Наиболее точный приближенный метод решения этой
задачи разработан В. А. Фоком. При большом числе электронов возникает возможность рассматривать электронную оболочку как своеобразную газовую атмосферу, окутывающую ядро, так же как обычная атмосфера окутывает землю. Благодаря огромной плотности электронов (порядка частиц на ) электронный газ в атоме вырожден, так же как и в твердом теле, и подчиняется статистике Ферми-Дирака. Указанная модель, предложенная Томасом и Ферми, дает возможность получить закон распределения плотности электронов в атоме и рассчитать ряд важных атомных характеристик в неплохом согласии с опытными данными.
Для щелочных металлов дело облегчается тем, что все электронное облако как бы распадается на две части: внешний валентный электрон и плотный атомный остаток, состоящий из остальных электронов и атомного ядра. Например, у атома натрия в состав атомного остатка входят десять электронов, а одиннадцатый электрон, слабо связанный с атомом, — валентный.
Рис. 255. Проникающая орбита.
Схема энергетических уровней атома щелочного металла может быть объяснена, если предположить, что при оптических переходах изменяется движение только валентного электрона, т. е. что только валентный электрон переходит с одной орбиты на другую. Электроны атомного остатка продолжают двигаться при этом по неизменным орбитам. Но на движении валентного электрона, конечно, сказывается существование электронов атомного остатка. Прежде всего электроны атомного остатка частично экранируют положительный заряд ядра. Поскольку заряд электронов остатка на единицу меньше заряда ядра, то результирующий положительный заряд атомного остатка будет равен единице (в ), так же как у ядра атома водорода. Этим единичным зарядом и определяется кулонова сила, действующая на валентный электрон.
Однако при своем движении по вытянутой орбите валентный электрон может «нырять» в атомный остаток (рис. 255). Такие орбиты называются проникающими. Ясно, что при движении валентного электрона на участке орбиты внутри атомного остатка величина кулоновой силы резко возрастает, так как уменьшается экранирующее действие остальных электронов. При движении валентного электрона по орбите, не проникающей в атомный остаток, на него действуют две силы: такая же кулонова сила, как и в атоме водорода, и сила притяжения электрическим диполем, возникающим в атомном остатке. Ведь атомный остаток (рис. 256) не только действует на оптический электрон, но и сам находится в электрическом поле этого электрона. Так как атомный остаток состоит из тяжелого положительного ядра и легкого облака электронов, то под
действием поля оптического электрона это электронное облако сдвигается в противоположную сторону, центр положительного заряда уже не совпадает с центром отрицательных зарядов и в результате атомный остаток поляризуется и приобретает дипольный момент.
Величина дипольного момента пропорциональна напряженности электрического поля оптического электрона, т. е. обратно пропорциональна квадрату расстояния от этого электрона до атомного остатка. Сила, с которой диполь действует на заряд, пропорциональна моменту диполя и обратно пропорциональна кубу расстояния (т. II, § 4, 1959 г.; в пред. изд. § 3).
Рис. 256. Поляризация атомного остатка
Рис. 257. Прецессия орбиты
Таким образом, дополнительная сила притяжения, действующая на электрон в атомах щелочных металлов и вызванная поляризацией атомного остатка, должна быть обратно пропорциональна пятой степени расстояния между электроном и атомным остатком (практически ядром).
Дополнительная сила вызывает прецессию электронной орбиты, что, конечно, влияет на энергию атома. Орбита вращается в своей плоскости вокруг атомного остатка как центра (рис. 257). Скорость этого вращения гораздо больше, чем в случае водорода, где прецессия орбиты вызывается непостоянством массы, поэтому и изменения энергии, вызванные прецессией, в атомах щелочных металлов больше, чем у водорода.
Расстояние между электроном и ядром изменяется при движении электрона по орбите, но среднее значение этого расстояния зависит от квантовых чисел При постоянном с ростом I орбита становится все более выпуклой, следовательно, среднее расстояние возрастает. Поскольку кулонова сила обратно пропорциональна квадрату расстояния, а дополнительная сила — пдтой степени, то с ростом среднего расстояния роль дополнительной силы в движении электрона должна быстро падать. Наоборот, чем меньше
, т. е. чем более вытянута орбита, тем больше роль этой силы и тем сильнее энергетическое состояние атома отличается от соответствующего состояния атома водорода. Одному и тому же значению главного квантового числа будет соответствовать ряд энергетических состояний атома щелочного металла с различными значениями азимутального квантового числа
На основании изложенных соображений ясно, что с ростом при постоянном I энергетические состояния должны приближаться к водородным (растут размеры орбиты, рис. 258).
Рис. 258. Сопоставление энергетических уровней натрия и водорода (уровням атома водорода соответствуют горизонтальные пунктирные линии),
Изменения энергии, вызванные поляризацией атомного остатка, приводят к тому, что энергия атома щелочного металла уже не может быть обратно пропорциональна квадратам целых чисел, как у атома водорода.
Тем самым находят свое объяснение поправки в выражениях для термов. Поправка 5 соответствует значению поправка значению значению значению Чем больше тем меньше, согласно сказанному выше, величина поправки.
Однако наряду с фактами, хорошо укладывающимися в описанную выше картину, мы встречаемся с фактами, которые как будто резко противоречат ей.
Щелочные металлы принадлежат, как известно, к числу легко ионизуемых веществ. Потенциал ионизации любого щелочного металла в несколько раз ниже потенциала ионизации водорода (см. таблицу). Иными словами, у атомов щелочных металлов гораздо легче оторвать валентный электрон, чем единственный электрон у атома водорода. Но ведь в атоме щелочного металла на валентный электрон действует дополнительная сила притяжения (связанная с поляризацией атомного остатка), т. е. он должен быть связан с атомным остатком сильнее, чем в атоме водорода. Это противоречие разрешается очень просто, если мы вспомним о принципе Паули, согласно которому происходит распределение электронов по орбитам (§ 60). Валентный электрон атома щелочного металла никогда не может оказаться на орбите с главным квантовым числом, равным единице, ибо эта орбита уже занята электронами атомного остатка. У атома водорода энергия ионизации определялась
для электрона, находящегося на первой орбите, что соответствует нормальному энергетическому состоянию. У лития наименьшее главное квантовое число валентного электрона 2, у натрия 3, калия 4, рубидия 5 и цезия 6. Энергии, необходимые для отрыва электрона, вращающегося в атоме водорода на орбитах с соответствующими главными числами, будут меньше энергий ионизации щелочных металлов. Чтобы убедиться в этом, достаточно разделить значение энергии ионизации атома водорода на квадраты главных квантовых чисел и сравнить результаты с цифрами таблицы.
Потенциалы ионизации атомов щелочных металлов
Для записи термов щелочных металлов вначале пользовались чисто эмпирическими формулами, приведенными на стр. 308, но в настоящее время применяют формулы, содержащие истинное значение главного квантового числа. Нормальное состояние атома щелочного металла обладает энергией, которую можно записать в виде
где постоянная Ридберга, имеет указанные выше значения для различных атомов щелочных металлов, поправка отрицательна, что соответствует понижению энергетического уровня по отношению к водороду, т. е. упрочению связи электрона. При этом уже представляет по абсолютной величине неправильную дробь. Соответственно изменяется нумерация остальных состояний.
На рис. 259 изображена схема энергетических уровней натрия. В ней в каждом вертикальном столбце собраны энергетические состояния с одним и тем же азимутальным квантовым числом т. е. орбиты с одинаковым вращательным моментом. В каждом столбце главное квантовое числа изменяется от наименьшего значения до бесконечности. Для сравнения рядом изображены соответствующие уровни атома водорода (обратите внимание на сильный сдвиг вниз соответствующих уровней натрия).
Все состояния с обозначаются буквой буквой буквой буквой Если мы хотим
обозначить состояние с определенным главным квантовым числом , мы пишем, например, или
Косыми линиями изображены переходы, соответствующие наблюдаемым на опыте спектральным линиям.
Рис. 259. (см. скан) Полная схема уровней натрия.
Нетрудно видеть, что эти Переходы удовлетворяют правилу отбора, согласно которому при оптических переходах I может изменяться только на ± 1, т. е. переходы могут происходить только
между соседними столбцами. Так же как и у водорода, спектр щелочных металлов распадается на несколько серий линий, называемых: главная серия, первая побочная (диффузная), вторая побочная (резкая) и серия Бергмана.
На рис. 254 сверху изображен полный спектр натрия, а под ним — отдельные спектральные серии, на которые его можно разбить. Каждая серия, как и в случае водорода, излучается в результате переходов с различных верхних уровней на один и тот же нижний уровень.
Главная серия представляет собой переходы с -уровней на уровень (обозначение термов происходит от латинского слова principale - главный).
Первая побочная серия представляет собой переходы с -уровней на уровень (обозначение термов также происходит от названия серии diffuse - диффузная).
Вторая побочная серия представляет собой переходы с -уровней на тот же уровень (обозначение терма происходит от названия scharf - резкая).
Наконец, серия Бергмана (фундаментальная) представляет собой переходы с -уровней на уровень (обозначение происходит от названия серии fundamental - фундаментальная).
С возрастанием спектральные линии каждой серии располагаются все ближе и ближе друг к другу, также как в спектре водорода, причем очевидно, что диффузная и резкая серии имеют общий предел (при так как обе эти серии соответствуют переходам на один и тот же нижний уровень
Предельная частота главной серии определяет энергию ионизации атома щелочного металла в нормальном состоянии.
При возбуждении свечения паров щелочных металлов в первую очередь возбуждается головная линия главной серии. Эта линия характерна для свечения данного металла и носит название резонансной. К числу таких линий принадлежит желтая линия натрия с длиной волны красная линия лития 670 ммк, красная линия калия 768 ммк и т. д.
При более детальном исследовании спектра щелочных металлов обнаруживается замечательная особенность их строения. Каждая линия спектра при достаточной дисперсии разделяется на две или на три, причем у более тяжелых металлов компоненты раздвинуты дальше друг от друга. Например, у линий калия расстояние между компонентами линий больше, чем у натрия. Спектральные линии, состоящие из двух компонент, носят название дублетов. Указанная выше желтая линия натрия также является дублетом и состоит из двух линий: красная линия калия: 7699 А и 7665 А. Мы видим, что действительно у натрия разность длин волн равна тогда как у калия т. е. почти в 6 раз больше. Возникает вопрос, как связать это расщепление линий с энергетическими
характеристиками атома? Следует иметь в виду, что всякое усложнение спектра связано с усложнением и уточнением этих характеристик. Очевидно, две компоненты одного дублета соответствуют переходу между двумя различными парами уровней, причем это различие между уровнями весьма невелико. Можно сказать, что вместо прежних простых уровней здесь имеются комбинации раздвоенных энергетических уровней атома, дающих соответственно раздвоенные спектральные линии. Для правильного выражения спектра щелочного металла все термы, кроме -термов, надо считать двойными (рис. 259).
Очевидно, что мы еще не учли всех факторов, определяющих энергию атома. Д. С. Рождественским в 1919 г. было высказано оправдавшееся впоследствии предположение о том, что здесь сказываются изменения магнитной энергии атома. Для правильного учета этого фактора необходимо допустить существование магнитного момента электрона. Как было указано в § 59, электрон, кроме электрического заряда, обладает магнитным моментом, который, грубо говоря, возникает вследствие его вращения вокруг собственной оси.
При движении электрона по орбите энергия атома зависит от того, совпадает ли направление магнитного момента электрона с направлением магнитного момента орбиты или они направлены в противоположные стороны. В первом случае магнитные моменты орбиты и электрона складываются, во втором — вычитаются, чем и обусловливается разность энергий обоих состояний, соответствующих одной и той же орбите. Вследствие малости магнитного момента, которым обладает электрон, разность энергий двух таких уровней будет невелика, причем ниже будет расположен уровень с противоположно направленными моментами. Дублетная линия соответствует двум переходам — или с двух уровней на один общий, или с одного уровня на два.
Из анализа спектров щелочных металлов выяснилось, что все их энергетические уровни двойные, кроме -уровней. Следовательно, если электрон находится на -орбите, то ориентировка его спина не играет роли. Это может быть только в том случае, если момент количества движения -орбиты равен нулю, ибо только в этом случае отсутствует магнитное поле, создаваемое орбитальным движением, и нет никакого смысла говорить об ориентировке момента электрона по отношению к моменту орбиты. Таким образом, мы приходим к необходимости считать момент количества движения -орбиты равным нулю, что противоречит модели атома Бора и согласуется с выводами волновой механики (§ 64).
Результирующий механический момент атома, равный векторной сумме орбитального и собственного моментов, будет характеризоваться квантовыми числами равными или , в
зависимости от ориентации спина (§ 59). Соответственно усложняется символика, применяемая для обозначения энергетических состояний атома щелочного металла, например двойка слева наверху указывает, что уровень дублетный, индекс справа внизу обозначает полный момент; очевидно, могут существовать состояния
В нормальном состоянии атомы щелочных металлов находятся на -уровне: их орбитальный момент равен нулю и, следовательно, результирующий момент атомов в целом равен просто спину электрона.
Представление о спине электрона впервые было выдвинуто Юленбеком и Гаудсмитом в 1925 г. как раз для объяснения структуры спектра щелочных металлов. Теория Юленбека и Гаудсмита дает правильный закон для расстояния между компонентами дублета в зависимости от эффективного заряда ядра.
Таким образом, анализ спектров щелочных металлов привел к открытию чрезвычайно важного свойства электрона. В дальнейшем выяснилась огромная роль электронного спина в явлении химической связи атомов, в электрических и магнитных свойствах твердых тел и т. п. Спин не менее важная характеристика электрона, чем его заряд.
Несмотря на то, что из структуры спектров совершенно непреложно вытекает необходимость существования электронного магнитного момента, все же представляют весьма значительный интерес непосредственное экспериментальное обнаружение этого момента и определение его величины. К сожалению, из волновых свойств электрона вытекает невозможность определения этой величины у свободных электронов, и поэтому речь может идти только об определении спина связанных электронов, входящих в состав атома.
Рис. 260. Силы, действующие на элементарный магнитик в неоднородном и однородном магнитных полях.
Мы уже указывали, что магнитный момент атома щелочного металла в нормальном состоянии равен магнитному моменту электрона.
Штерн и Герлах в 1921 г. осуществили чрезвычайно изящный опыт, в котором удалось определить магнитный момент отдельных атомов. Метод Штерна и Герлаха основан на том, что поток частиц, обладающих магнитными моментами, должен отклоняться в неоднородном магнитном поле. Если мы представим себе отдельную частицу в виде элементарного магнитика, то в однородном магнитном поле такие магнитики будут только поворачиваться, так как на оба полюса (рис. 260) будут действовать равные, но противоположно направленные силы. Иначе дело будет происходить в неоднородном магнитном поле, напряженность которого имеет разные значения в точках Тогда силы действующие на магнит, уже не равны друг другу, и он будет двигаться в направлении большей силы.
Рис. 261. Опыт Штерна — Герлаха,
В опытах Штерна и Герлаха пучок атомов серебра в нормальном состоянии, испаряющихся из печки пролетал между полюсами электромагнита, образующими благодаря своей форме сильно неоднородное магнитное поле, и попадал на пластинку Атомы осаждались на пластинке давая на ней пятно (рис. 261).
При наложении магнитного поля пятно раздваивалось, что соответствовало раздвоению атомного пучка. Это раздвоение объясняется
тем, что магнитный момент атома может быть в данном случае ориентирован только либо параллельно, либо антипараллельно полю (так же как момент электрона по отношению к полю орбиты атома). Различным ориентациям соответствуют различные отклонения атомов в магнитном поле, что и приводит к раздвоению пучка. Таким образом, опыт Штерна и Герлаха непосредственно доказывает существование пространственного квантования.
Из расстояния между пятнами можно определить магнитный момент атома, равный электронному моменту у щелочных металлов. Таким способом удалось прямо доказать, что магнитный момент электрона действительно равен магнетону Бора, т. е.
Читайте также:
