Формула эйлера справедлива для стальных колонн с гибкостью
Обновлено: 04.05.2024
Как показали опыты, решение Эйлера подтверждается не во всех случаях. Причина состоит в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень работает в пределах упругих деформаций по закону Гука. Следовательно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности. В связи с этим найдем границы применимости решения Эйлера:
Из (30) следует, что напряжениеФормула Эйлера неприемлема, если напряжения
гдеЕсли λ > λпред , то формулу Эйлера можно применять. В противном случае ею пользоваться нельзя. Для стали Ст. 3 – lпред = 100.
В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится нелинейной. В связи с этим, в таких случаях пользуются эмпирическими зависимостями. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:
где a, b – постоянные, зависящие от материала, так для стали Ст. 3 a = 3,1•10 5 кН/м2, b = 11,4•10 2 кН/м2.
Когда формула Эйлера неприменима (за пределом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.
здесь a и b коэффициенты, зависящие от материала стержня, измеряются в МПа, приводятся в справочниках, для ст. 3:
a = 310 МПа, b = 1,14 МПа.
Некоторые термины:
Брус - тело, продольные размеры которого значительно превышают его поперечные размеры.
А) Заделка — нет перемещений (жесткое закрепление тела, например, сварка), возникают реакция неизвестной величины и направления R и реактивный момент MR.
Б) Неподвижная шарнирная опора — возможно вращение вокруг опоры, линейных перемещений нет, поэтому возникает реакция неизвестной величины и направления R, которую заменяют ее проекциями на оси координат. Для плоской системы возникают 2 неизвестные реакции: R1 и R2.
В) Подвижная шарнирная опора — возможно вращение вокруг опоры и перемещение вдоль одной из осей, например, плавающая подшипниковая опора, возникает одна реакция R: сила в направлении ограничения движения


Напряжение(обозначается р).
Напряжение характеризует интенсивность внутренних сил, действующих в сечении, и определяется, как отношение величины внутренней силы к площади сечения.
Напряжение является величиной векторной.
Вектор напряжения можно разложить на две составляющие – одну вдоль оси сечения, вторую – в плоскости сечения (перпендикулярно оси). Эти составляющие носят название нормальное напряжение(обозначается σ) и касательное напряжение(обозначается τ).
Поскольку нормальные и касательные напряжения расположены под прямым углом друг к другу, модуль полного напряжения p можно определить по теореме Пифагора:
р 2 = σ 2 + τ 2
Размерности:1 Мпа = 1 кН / см 2
Центр масс —геометрическая точка, характеризующая движение тела или системы частиц как целого.
Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю.
В основном последние два понятия совпадают, но не всегда. Например (для лучшего осмысления понятия центра тяжести) :В системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.
Угол поворота- угловое перемещение в радианах.
Если φ — угловое перемещение в радианах, s — длина дуги, заключенной между сторонами угла поворота, r — радиус
φ =s / r = радиан.
Вал– вращающийся стержень.
| Практический метод расчета на устойчивость. |
В основу рачетов сжатых стержней на устойчивость положено требование, согласно которому допустимое напряжение должно быть меньше не только предела текучести  . |
Разделив предел текучести при сжатии  на коэффициент запаса по текучести nт получим допустимое напряжение на сжатие для коротких стержней (типа образцов): |
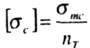 |
Теперь это допустимое напряжение надо еще уменьшить, чтобы оно было меньше  . Но критическое напряжение  зависит от гибкости стержня  (чем больше  , тем меньше  ) и от материала стойки. Эти факторы учтены в 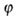 -коэффициенте понижения допускаемых напряжений. Коэффициент 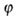 берется из таблиц в зависимости от  и материала. |
| Допускаемая сжимающая сила для гибкого стержня определяется по формуле |
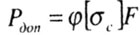 |
где 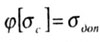 - допустимое сжимающее напряжение с учетом устойчивости. |
На рис. 8.3 пунктиром дан график зависимости допустимого напряжения ояоп от гибкости стойки  . |
| Различают прямую и обратную задачу проектировочного расчета. |
σпц - предел пропорциональности – справедлив закон Гука
Определяется как крайняя верхняя точка начального прямолинейного участка диаграммы.
σу – предел упругости, это когда выполняется закон Гука, но остаточная деформация приобретает 0.05 % от начальной длины
σТ - предел текучести – когда начинается пластическая деформация
Точка после которой линия диаграммы некоторое время движется параллельно оси деформаций ε.
Практически горизонтальный участок диаграммы, следующий за пределом текучести называется площадкой текучести.
σпч - предел прочности (σв - временное сопротивление) – когда происходит разрыв образца
Высшая точка условной диаграммы;
σр - напряжение в момент разрыва образца (σр у - условное и σр и - истинное)
Конечная точка диаграммы, при которой происходит разрыв образца.
- условное напряжение разрыва
- истинное напряжение при разрыве
здесь Aш - площадь поперечного сечения в области "шейки" образца.
Следует помнить, что предел текучести есть ТОЛЬКО у пластичных материалов.
Ухрупких материалов условный предел текучести σ0,2 (читается: сигма ноль-два), который соответствует напряжению, при котором остаточная (пластическая деформация) составляют 0,2 % от длины испытываемого образца.
Формула эйлера справедлива для стальных колонн с гибкостью
Казалось бы, что полученные в предыдущих параграфах результаты решают задачу проверки сжатого стержня на устойчивость; остается выбрать лишь коэффициент запаса . Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.
На рис.1 приведена зависимость величины критических напряжений, вычисленных при различных значениях гибкости для стали 3, обычно применяемой в металлических конструкциях. Эта зависимость представляется гиперболической кривой, так называемой «гиперболой Эйлеpa»:
При пользовании этой кривой надо вспомнить, что представляемая ею формула получена при помощи интегрирования дифференциального уравнения изогнутой оси, т. е. в предположении, что напряжения в стержне в момент потери устойчивости не превосходят предела пропорциональности.
Рис.1. Гиперболическая зависимость критического напряжения от гибкости стержня
Следовательно, мы не имеем права пользоваться величинами критических напряжений, вычисленных по формуле Эйлера, если они получаются выше этого предела для данного материала. Иначе говоря, формула Эйлера применима лишь при соблюдении условия:
Если из этого неравенства выразить гибкость , то условие применимости формул Эйлера получит иной вид:
Подставляя соответствующие значения модуля упругости и предела пропорциональности для данного материала, находим наименьшее значение гибкости, при которой еще можно пользоваться формулой Эйлера. Для стали 3 предел пропорциональности может быть принят равным , поэтому, для стержней из этого материала можно пользоваться формулой Эйлера лишь при гибкости
т. е. большей, чем 100 %
Для стали 5 при формула Эйлера применима при гибкости ; для чугуна при , для сосны при и т. д. Если мы на Рис.1 проведем горизонтальную линию с ординатой, равной , то она рассечет гиперболу Эйлера на две части; пользоваться можно лишь нижней частью графика, относящейся к сравнительно тонким и длинным стержням, потеря устойчивости которых происходит при напряжениях, лежащих не выше предела пропорциональности.
Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.
Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.
Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т. е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.
Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 3040; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.
Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести (при пластичном материале) или предела прочности (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 3040, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или (сталь), или (чугун, дерево).
Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.
В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала вызывают небольшие прогибы и при сжимающих силах, меньших критических.
Подобный же характер имеет и зависимость укорочений от напряжения при сжатии коротких стержней; мы имеет ту же внезапность роста деформаций при определенной величине напряжений (когда ).
Нам остается теперь рассмотреть поведение сжатых стержней при средних величинах гибкости, например для стальных стержней при гибкостях от 40 до 100; с подобными значениями гибкостей инженер чаще всего встречается на практике.
По характеру разрушения эти стержни приближаются к категории ^ тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.
Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.
Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.
На основании полученного опытного материала можно считать, что при критических напряжениях, меньших предела пропорциональности, все эксперименты подтверждают формулу Эйлера для любого материала.
Для стержней средней и малой гибкости были предложены различные эмпирические формулы, показывающие, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному:
где а и b коэффициенты, зависящие от материала, a гибкость стержня. Для литого железа Ясинский получил: а = 338,7МПа, b = 1,483 МПа. Для стали 3 при гибкостях от = 40 до = 100 коэффициенты а и b могут быть приняты: а = 336 МПа; b = 1,47МПа. Для дерева (сосна): а = 29,3 МПа; b = 0,194 МПа.
Иногда удобны эмпирические формулы, дающие для неупругой области изменение критических напряжений по закону квадратной параболы; к ним относится формула
Здесь при = 0 считают для пластичного и для хрупкого материала; коэффициент а, подобранный из условия плавного сопряжения с гиперболой Эйлера, имеет значение:
для стали с пределом текучести = 280 МПа а = 0,009 МПа
сосны прочности = 30; а = 0,0008 »
чугуна = 420; а = 0,044 »
При наличии приведенных здесь данных может быть построен полный график критических напряжений (в зависимости от гибкости) для любого материала. На Рис.2 приведен такой график для строительной стали с пределом текучести и пределом пропорциональности .
Рис.2. Полный график критических напряжений для строительной стали.
График состоит из трех частей: гиперболы Эйлера при, наклонной прямой при и горизонтальной, или слабо наклонной, прямой при . Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.
Таким образом, можно считать, что задача определения критических напряжений для стержней любой гибкости решена с достаточной для практических целей точностью.
Проверка сжатых стержней на устойчивость.
Ранее было отмечено, что для сжатых стержней должны быть произведены две проверки:
Для установления допускаемого напряжения на устойчивость нам остается теперь выбрать только коэффициент запаса k.
На практике этот коэффициент колеблется для стали в пределах от 1,8 до 3,0. Коэффициент запаса на устойчивость выбирается выше коэффициента запаса на прочность, равного для стали 1,5 1,6.
Это объясняется наличием ряда обстоятельств, неизбежных на практике (начальная кривизна, эксцентриситет действия, нагрузки, неоднородность материала и т. д.) и почти не отражающихся на работе конструкции при других видах деформации (кручение, изгиб, растяжение).
Для сжатых же стержней, ввиду возможности потери устойчивости, эти обстоятельства могут сильно снизить грузоподъемность стержня. Для чугуна коэффициент запаса колеблется от 5,0 до 5,5, для дерева от 2,8 до 3,2.
Чтобы установить связь между допускаемым напряжением на устойчивость [] и допускаемым напряжением на прочность [], возьмем их отношение:
Рис.3. Расчетная схема сжатой стойки.
Так как в условии устойчивости нам не известно ни , ни , одной из этих величин необходимо задаться. Примем для первого приближения . В этом случае необходимая площадь поперечного сечения стержня будет равна
По сортаменту выбираем двутавр No 24, b с площадью . Наименьший радиус инерции сечения . Соответствующая гибкость стойки
Коэффициент по интерполяции между значениями его из таблицы для и равен . Расчетным напряжением будет:
Перенапряжение составляет. Подбираем двутавр No 27, а. ; ; наибольшая его гибкость . Так как коэффициент , то расчетное напряжение
Значениям критической силы высших порядков соответствуют искривления по синусоидам с двумя, тремя и т. д. полуволнами (Рис.1):
Таким образом, чем больше точек перегиба будет иметь синусоидально-искривленная ось стержня, тем большей должна быть критическая сила. Более полные исследования показывают, что формы равновесия, определяемые формулами (1), неустойчивы; они переходят в устойчивые формы лишь при наличии промежуточных опор в точках В и С (рис.1).
Таким образом, поставленная задача решена; для нашего стержня наименьшая критическая сила определяется формулой
а изогнутая ось представляет синусоиду
Величина постоянной интегрирования а осталась неопределенной; физическое значение ее выяснится, если в уравнении синусоиды положить ; тогда (т. е. посредине длины стержня) получит значение:
Значит, а это прогиб стержня в сечении посредине его длины. Так как при критическом значении силы Р равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб f остался неопределенным.
Он должен быть при этом настолько малым, чтобы мы имели право применять приближенное дифференциальное уравнение изогнутой оси, т. е. чтобы было по прежнему мало по сравнению с единицей.
Получив значение критической силы, мы можем сейчас же найти и величину критического напряжения , разделив силу на площадь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для входит момент инерции поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчет полную, а не ослабленную, площадь поперечного сечения стержня . Тогда
Таким образом, критическое напряжение для стержней данного материала обратно пропорционально квадрату отношения длины стержня к наименьшему радиусу инерции его поперечного сечения. Это отношение называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость.
Из последнего выражения видно видно, что критическое напряжение при тонких и длинных стержнях может быть весьма малым, ниже основного допускаемого напряжения на прочность . Так, для стали 3 с пределом прочности допускаемое напряжение может быть принято ; критическое же напряжение для стержня с гибкостью при модуле упругости материала будет равно
Таким образом, если бы площадь сжатого стержня с такой гибкостью была подобрана лишь по условию прочности, то стержень разрушился бы от потери устойчивости прямолинейной формы.
Влияние способа закрепления концов стержня.
Формула Эйлера была получена путем интегрирования приближенного дифференциального уравнения изогнутой оси стержня при определенном закреплении его концов (шарнирно-опертых). Значит, найденное выражение критической силы справедливо лишь для стержня с шарнирно-опертыми концами и изменится при изменении условий закрепления концов стержня.
Закрепление сжатого стержня с шарнирно-опертыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем приводить' к основному случаю.
Если повторить весь ход вывода для стержня, жестко защемленного одним концом и нагруженного осевой сжимающей силой на другом конце (Рис.2), то мы получим другое выражение для критической силы, а следовательно, и для критических напряжений.
Рис.2. Расчетная схема стержня с жесткозакрепленным одним концом.
Предоставляя право студентам проделать это во всех подробностях самостоятельно, подойдем к выяснению критической силы для этого случая путем следующих простых рассуждений.
Пусть при достижении силой Р критического значения колонна будет сохранять равновесие при слабом выпучивании по кривой АВ. Сравнивая два варианта изгиба видим, что изогнутая ось стержня, защемленного одним концом, находится совершенно в тех же условиях, что и верхняя часть стержня двойной длины с шарнирно-закрепленными концами.
Значит, критическая сила для стойки длиной с одним защемленным, а другим свободным концами будет та,же, что для стойки с шарнирно-опертыми концами при длине :
Если мы обратимся к случаю стойки, у которой оба конца защемлены и не могут поворачиваться (Рис.3), то заметим, что при выпучивании, по симметрии, средняя часть стержня, длиной , будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).
Рис.3. Расчетная схема с жесткозакреплеными торцами.
Поэтому критическая сила для стержня с защемленными концами, длиной , равна критической силе для стержня основного случая длиной :
Полученные выражения можно объединить с формулой для критической силы основного случая и записать:
здесь так называемый коэффициент длины, равный:
при шарнирных концах (основной случай) ,
одном свободном, другом защемленном ,
обоих защемленных концах .
Для стержня, изображенного на рис.4, с одним защемленным, а другим шарнирно-опертым концами, коэффициент оказывается примерно равным , а критическая сила:
Рис.4. Потеря устойчивости стержня с одним жесткозакрепленным и другим шарнирно-опорным торцом
На практике, однако, почти никогда не встречаются в чистом виде те закрепления концов стержня, которые мы имеем на наших расчетных схемах.
Вместо шаровых опор обычно применяются цилиндрические шарниры. Подобные стержни следует считать шарнирно-опертыми при выпучивании их в плоскости, перпендикулярной к оси шарниров; при искривлении же в плоскости этих осей концы стержней следует считать защемленными (с учетом оговорок, приведенных ниже для защемленных концов).
В конструкциях очень часто встречаются сжатые стержни, концы которых приклепаны или приварены к другим элементам, часто еще с добавлением в месте прикрепления фасонных листов. Такое закрепление, однако, трудно считать защемлением, так как части конструкции, к которым прикреплены эти стержни, не являются абсолютно жесткими.
Между тем, достаточно возможности уже небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях, очень близких к шарнирному опиранию. Поэтому на практике недопустимо рассчитывать такие стержни, как стойки с абсолютно защемленными концами. Лишь в тех случаях, Когда имеет место очень надежное защемление концов, допускается небольшое (процентов на 1020) уменьшение свободной длины стержня.
Наконец, на практике встречаются стержни, опирающиеся на соседние элементы по всей плоскости опорных поперечных сечений. Сюда относятся деревянные стойки, отдельно стоящие металлические колонны, притянутые болтами к фундаменту, и т. д. При тщательном конструировании опорного башмака и соединения его с фундаментом можно считать эти стержни имеющими защемленный конец. Сюда же относятся мощные колонны с цилиндрическим шарниром при расчете их на выпучивание в плоскости оси шарнира. Обычно же трудно рассчитывать на надежное и равномерное прилегание плоского концевого сечения сжатого стержня к опоре. Поэтому грузоподъемность таких стоек обычно мало превышает грузоподъемность стержней с шарнирно-опертыми концами.
Значения критических нагрузок могут быть получены в виде формул типа эйлеровой и для стержней переменного сечения, а также при действии нескольких сжимающих сил.
Техническая механика
Продольным изгибом называется изгиб первоначально прямолинейного стержня вследствие потери устойчивости под действием центрально приложенных продольных сжимающих сил. Продольный изгиб возникает при достижении сжимающими силами и напряжениями критического значения.

Расчеты на прочность и жесткость, выполняемые для большинства видов деформаций основываются на предположении, что между внешними нагрузками и вызываемыми ими внутренними силами существует устойчивая форма равновесия, при которой малым возмущающим воздействиям соответствуют малые отклонения конструкции от первоначальной формы.
Нагрузки, при превышении которых происходит потеря устойчивости (критическое состояние), называют критическими нагрузками.
Примером явления продольного изгиба может послужить длинная школьная линейка, к одному из концов которой приложена сжимающая сила. Сначала материал линейки сопротивляется нагрузке, и линейка работает, как обычный сжимаемый брус. Затем, по достижении определенной нагрузки, линейка начинает прогрессирующе изгибаться без существенного увеличения сжимающей силы и теряет устойчивость (т. е. гнется без заметных усилий вплоть до поломки).
Явление продольного изгиба можно объяснить тем, что к реальному стержню практически невозможно применить основные гипотезы и допущения сопромата - об однородности, изотропности и непрерывности материала. Поэтому при продольном сжатии стержня, даже если сжимающая сила приложена идеально вдоль его оси (что тоже на практике нереально), отдельные волокна этого стержня неодинаково сопротивляются сжатию (из-за неоднородности и анизотропии материала, из которого он изготовлен). В результате, при достижении сжимающей силой критической величины, стержень начинает изгибаться в сторону наименьшего сопротивления волокон.
На практике этому способствует, также, приложение нагрузки не строго вдоль центральной оси сечения. По мере увеличения изгиба и потери стержнем устойчивости возрастают изгибающие нагрузки, поскольку, чем сильнее изгибается стержень, тем дальше от его оси отклоняется линия действия сжимающей силы, образуя возрастающий момент изгиба. По этой причине стержень изгибается все сильнее даже при небольшом возрастании сжимающей силы (прогрессивно растет плечо изгибающего момента этой силы).
В конечном итоге стержень теряет устойчивость, что чаще всего сопровождается его поломкой или неупругой деформацией (безвозратной потерей прямолинейности или начальной формы).
Если предположить, что материал стержня идеально соответствует принимаемым в сопромате допущениям и гипотезам, а сжимающая сила приложена строго к центру тяжести сечения вдоль оси стержня, то такой стержень будет работать на простое сжатие, и разрушится не из-за потери устойчивости, а из-за превышения предельных прочностных характеристик для сжатия. Если же стержень имеет сечение в виде сложной фигуры, то решающую роль при потере устойчивости играет отклонение продольной нагрузки от главной центральной оси этой фигуры.

Опасность потери устойчивости особенно велика для тонкостенных конструкций, стержней, пластинок и оболочек.
Рассмотрим тонкий стальной стержень, длина которого значительно больше поперечных размеров, сжимаемый силой F , немного большей критической силы Fкр (см. рисунок 1) .
Применяя метод сечений, убеждаемся, что в результате искривления оси в поперечных сечениях стержня возникают два внутренних силовых фактора – продольная сила N = F и изгибающий момент Ми .
Таким образом, искривленный стержень испытывает сочетание деформаций центрального сжатия и изгиба.
При сжимающих силах, даже немного превышающих критическую силу, напряжения изгиба могут непосредственно угрожать прочности конструкции. Поэтому критическое состояние конструкции считается недопустимым.
Для обеспечения устойчивости необходимо, чтобы действующая на стержень сжимающая сила F была меньше критической Fкр . Обозначим допускаемую сжимающую силу [F] , тогда:
где: [sy] – допускаемый коэффициент запаса устойчивости.
Очевидно, что устойчивость стержня обеспечена, если [sy] > 1.
Значение коэффициента запаса устойчивости зависит от назначения стержня и его материала. Обычно для сталей [sy] = 1,8….3; для чугунов [sy] = 5….5,5; для дерева [sy] = 2,8….3,2.
Формулы Эйлера и Ясинского для расчетов стержней на устойчивость
Леонард Эйлер (Leonhard Euler, 1707 - 1783) - выдающийся ученый, которого в разных источниках называют швейцарским, немецким и российским. Математик, физик, астроном и механик, внёсший фундаментальный вклад в развитие этих и ряда других прикладных наук.
Эйлер - автор более чем 850 научных работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.
Академик Петербургской, Берлинской, Туринской, Лиссабонской и Базельской академий наук, иностранный член Парижской академии наук.
Л. Эйлер почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1726 по 1741, а также с 1766 года и до конца жизни был академиком Петербургской академии наук. С 1741 по 1766 год работал в Берлине (оставаясь одновременно почётным членом Петербургской академии).
Превосходно знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском.
Некоторые из потомков Л. Эйлера до сих пор живут в России.
Л. Эйлером была предложена формула для определения величины критической силы Fкр , которая приводится здесь без вывода:
где: Е – модуль упругости первого рода; Imin - наименьший из осевых моментов инерции сечения, поскольку искривление происходит в плоскости наименьшей жесткости; lп – приведенная длина стержня, которая может быть определена по формуле:
где: l – длина стержня; μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня.
Наиболее часто встречающиеся способы закрепления концов стержня и соответствующие им значения коэффициента приведения длины представлены на рисунке 2 .
Вывод формулы Эйлера основан на известном законе Гука, который справедлив лишь до предела пропорциональности. Поэтому формулой Эйлера можно пользоваться не всегда.
Для определения пределов применимости формулы Эйлера определим критическое напряжение σкр , т. е. напряжение, которое возникает в поперечном сечении площадью А стержня при достижении критической силы:
Определим наименьший радиус инерции imin поперечного сечения стержня:
imin = √(Imin / A) (здесь √ - знак квадратного корня) .
Перепишем формулу для σкр так:
Введем понятие гибкости стержня: λ = μl / imin . Это безразмерная величина, характеризующая размеры стержня и способ закрепления его концов. Окончательно получим:
σкр = π 2 Е / λ 2 .
Формулу Эйлера можно применять только при выполнении условия:
где: σпц – предел пропорциональности материала стержня. Следовательно, должно быть
λ ≥ √( π 2 Е / σпц) = λпред (здесь √ - знак квадратного корня) .

Величину, стоящую в правой части неравенства, называют предельной гибкостью. Предельная гибкость зависит только от физико-механических свойств материала стержня.
Условие применимости формулы Эйлера можно записать так: λ ≥ λпред , т. е. формула Эйлера применима лишь в тех случаях, когда гибкость стержня больше или равна предельной гибкости. Так, для стержней из низкоуглеродистой стали формула Эйлера применима, если их гибкость λ ≥ 100.
В тех случаях, когда гибкость стержней меньше предельной, формула Эйлера становится неприменимой и при расчетах пользуются эмпирической формулой Ясинского:
где: а и b – коэффициенты, зависящие от материала и определяемые по таблицам справочников.
Если стержень имеет гибкость λ ≤ 40, то его можно рассчитывать на простое сжатие по формуле σс = F / А .
Расчеты прямолинейных стержней на устойчивость
Существует три вида расчетов на устойчивость прямолинейных стержней – проектный, проверочный и силовой.
Проектный расчет заключается в определении минимального осевого момента инерции поперечного сечения стержня по формуле:
где: F - действующая нагрузка; [sy] – допускаемый коэффициент запаса устойчивости; μ – коэффициент приведения длины стержня; l – длина стержня; Е – модуль продольной упругости.
Далее находят гибкость стержня по формуле: λ = μl / imin ,
где: imin = √(Imin / A) , ( А – площадь сечения стержня) .
Полученную гибкость сравнивают с предельной для данного материала.
Проверочный расчет заключается в определении действительного коэффициента запаса устойчивости sy и сравнении его с допускаемым:
Силовой расчет заключается в определении допускаемой нагрузки [F] по формуле:
Расчет сжатых стержней на устойчивость можно свести к расчету на простое сжатие. При расчете применяют следующую формулу:
где: [σс] – допускаемое напряжение на сжатие; φ – коэффициент продольного изгиба (справочная величина, определяемая по таблицам).
Расчеты показывают, что при продольном изгибе наиболее выгодными являются кольцевые и коробочные тонкостенные сечения, имеющие относительно большой момент инерции.
4.4. Пределы применимости формулы Эйлера. Кривая критических напряжений
Формула Эйлера, полученная 260 лет назад, долгое время являлась предметом дискуссий, продолжавшихся до первых десятилетий XIXвека. Причиной споров являлось то обстоятельство, что она не всегда подтверждалась экспериментами. Были даже аварии мостов в связи с потерей устойчивости раскосов ферм, рассчитанных по формуле Эйлера. А дело было в том, что инженеры того времени не обратили внимание на некоторые ограничения по применению этой формулы, которые автор специально не оговаривал.
Вывод формулы Эйлера основан на применении дифференциального уравнения упругой линии. Поэтому пользоваться этой формулой можно лишь в том случае, если справедлив закон Гука, т.е. пока критическое напряжение (напряжение сжатия, соответствующее критической силе) не превышает предела пропорциональности.

. (4.11)
Если прямолинейная форма равновесия стержня остаётся устойчивой и при напряжениях, превышающих предел пропорциональности, то дифференциальное уравнение (4.1) не пригодно для описания изгиба при потере устойчивости.
Выведем формулу для критического напряжения σкр. Подставим (4.10) в (4.11) и получим

, (4.12)

где – квадрат наименьшего радиуса инерции стержня (см.(4.21) в первой части).
Вводя безразмерную величину

, (4.13)
называемую гибкостью стержня, окончательно получим:

. (4.14)
Из условия применимости формулы Эйлера (4.11) имеем:

,

. (4.15)
Найдём значение λпреддля стали марки Ст3 (самая распространённая пластичная сталь, из которой делают прокатные профили, металлоконструкции зданий и сооружений):Е = 2∙10 4 кН/см 2 , σПЦ = 20 кН/см 2 .

.
Таким образом, формула Эйлера справедлива только для гибких стержней.
Однако явление продольного изгиба существует не только при упругих, но и при упругопластических деформациях, когда критические напряжения больше предела пропорциональности σПЦ, но меньше предела текучестиσТ. Построим график зависимости критических напряженийσкрот гибкостиλдля стержней из стали Ст3 (рис.4.8).

Сначала построим кривую – гиперболу Эйлера – по формуле (4.14). Она начинается от точки с координатами σПЦ,λ = 100и уходит вправо в область больших гибкостей. Это область упругих деформаций.
Стержни малой гибкости (короткие и «толстые») потерять устойчивость не могут, а могут разрушиться (достигнуть предельного состояния) в общепринятом смысле (см.рис.4.1,а). Поэтому в диапазоне гибкостей 0 < λ ≤ 40 σкр = σТ– область пластических деформаций.
В диапазоне средних гибкостей 40 < λ < 100кривая критических напряжений представляет собой прямую линию, соединяющую крайние точкиσкр = σТиσкр = σПЦ. Это простое решение предложил русский учёный Ф.С.Ясинский на основании большого объёма экспериментальных исследований. Формула Ясинского имеет вид
σкр = a – bλ, (4.16)
где аиb– постоянные, зависящие от материала.
σкр = 31 – 0,114λ (σкр в кН/см 2 ).(4.17)
Это область упругопластических деформаций.
Если в этой области использовать формулу Эйлера (пунктирная линия), она даёт завышенные значения критических напряжений, т.е. всегда переоценивает действительную устойчивость стержня. Поэтому использование формулы Эйлера для стержней, теряющих устойчивость при упругопластических деформациях, не только принципиально неправильно, но и крайне опасно по своим последствиям.

Теоретическому решению этой проблемы было посвящено большое количество работ разных авторов. В настоящее время общепризнанным является решение немецкого учёного Ф.Энгессера, который предложил определять критическую силу в упругопластической стадии по формуле Эйлера, подставляя в неё вместо модуля упругости Е так называемый касательный модуль (рис.4.9).

. (4.18)
Сила Ркр(τ)называется касательно-модульной.
Кривая критических напряжений, подсчитанных по формуле (4.18), показана на рис.4.8 тонкой линией. Видим, что прямая Ясинского мало отличается от касательно-модульной кривой, причём даёт результат, повышающий запас устойчивости.
Читайте также:
