Как найти удлинение стального бруса

Обновлено: 09.05.2024

В конструкциях подвижного состава имеются элементы, работающие на растяжение или сжатие (иногда попеременно растяжение-сжатие). К ним относятся автосцепка, поводок буксы, элементы подвески экипажной части локомотивов, поршень и шток в цилиндре дизеля и др.

Формы и размеры этих элементов конструкций определяются необходимостью обеспечить их прочность при действии растягивающих или сжимающих усилий, возникающих в процессе работы подвижного состава.

К решению задач №№ 1-10 следует приступать после изучения темы 4.2 "Растяжение, сжатие" и внимательного изучения примера 9.

Растяжением (сжатием) называют такое нагружение бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор - продольная сила N.

Продольную силу определяем при помощи метода сечений.

Продольная сила N в любом поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на оставшуюся часть бруса.

Правило знаков: условимся внешние силы, растягивающие брус, считать положительными, а сжимающими его - отрицательными.

По известной продольной силе N и площади поперечного сечения А можно определить напряжения в этом сечении:

Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука

Условие прочности при растяжении и сжатии имеет вид

где σ, N - соответственно нормальное напряжение и продольная сила в опасном сечении (т.е. в сечении, где возникают наибольшие напряжения);

А - площадь поперечного сечения;

[σ] - допускаемое напряжение, т.е. максимальные значения напряжений, при которых гарантируется прочность детали. Исходя из условия прочности, можно решать три вида задач:

1) проверка прочности;

2) подбор сечения

3) определение допускаемой нагрузки [N] ≤ [σ] • А.

Для заданного на рис. 15 бруса построить эпюры продольных сил и нормальных напряжений, проверить прочность на каждом участке, приняв [σ]_р=160 МПа, [σ]_с=120 МПа, а также определить удлинение (укорочение) бруса, если модуль продольной упругости Е=2·10 5 МПа. Вес бруса не учитывать.

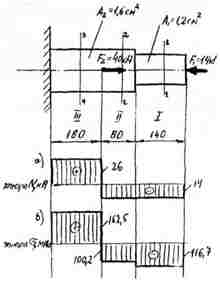
1. Разделим брус на участки, границы которых определяются местами изменения поперечных размеров бруса и точками приложения внешних нагрузок.

Рассматриваемый брус имеет три участка.

Для закрепленного одним концом бруса расчет целесообразно вести со свободного конца, чтобы не определять опорной реакции.

2. Применяя метод сечений, определяем продольную силу
N, выражая ее через внешние силы F₁ и F₂.

Проводя в пределах каждого из участков сечение, будем отбрасывать левую закрепленную часть бруса и оставлять для рассмотрения правую часть.

На участке I продольная сила равна

На участке II продольная сила равна

Отрицательное значение N показывает, что на участках I и II
- брус сжат. На участке III сила равна

Знак плюс показывает, что брус на III участке растянут.

По полученным из расчета данным строим эпюру N (рис. 15а).

Для этого параллельно оси бруса проведем базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения N. В пределах каждого участка нагружения продольная сила постоянная, а потому на эпюре изобразится прямой, параллельной базовой. Положительные значения будем откладывать вверх от базовой линии, а отрицательные - вниз. Эпюра штрихуется линиями, перпендикулярными оси бруса.

Эпюра продольных сил представляет собой график, выражающий закон изменения продольной силы во всей длине бруса.

Любая ордината эпюры продольных сил, измеренная в соответствующем масштабе, выражает величину продольной силы в данном поперечном сечении.

3. Для определения напряжений и в любом поперечном сечении значение продольной силы, действующей в данном сечении необходимо разделить на площадь этого сечения:

Находим напряжения на каждом участке бруса и строим эпюру:

В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений (рис. 156).

При построении эпюр и проверке их правильности следует руководствоваться следующими правилами:

1. Скачки на эпюрах N имеют место в точках приложения сосредоточенных сил. Величина скачка равна внешней силе, приложенной в этом сечении.

2. На эпюре а скачки имеют место не только в точках приложения сосредоточенных сил, но и в местах изменения площади поперечного сечения.

3. Знаки на участках эпюры а должны совпадать со знаками на соответствующих участках эпюры N.

4. Выполняем проверку прочности бруса, т.е. расчетное напряжение (для каждого участка в отдельности) сравниваем с допускаемыми:

На участке I имеет место небольшая недогрузка - 2,8%, на участке III - перегрузка составляет 1,5%.

Величины превышений от допускаемых напряжений в пределах 5% в реальном проектировании считаются возможными.

Поэтому на I и на III участках сечение подобраны верно.

На участке II недогрузка составляет 27% - это говорит о том, что сечение на участке II выбрано не экономично, имеет место большой перерасход материала, (>10%).

1. Полное удлинение можно найти, воспользовавшись эпюрой N, представленной на рис. 15а, т.е. полное удлинение бруса равно алгебраической сумме удлинений его участков:

Определим ∆l₁, ∆l₂, ∆l₃, используя формулу Гука:

∆l = 0,08 0,035 + 0,146 =0,029 мм

Полученный в ответе знак плюс говорит о том, что в целом брус удлинился, т.е. свободный брус переместился, в нашем случае вправо.

Техническая механика

На этой странице приведен еще один пример решения задачи по Сопромату, где необходимо найти внутренние усилия, напряжения и линейные удлинения на участках и в сечениях бруса, нагруженного продольной силой и собственным весом.

Результаты расчетов оформлены эпюрами продольных сил, напряжений и удлинений бруса.

Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).

Расчет стержня

Условие задачи:

Стержень, жестко закрепленный одним концом, состоящий из трех участков длиной l₁ … l₃ , и площадью А₁ … А₃ , находится под действием собственного веса и силы F , приложенной на координате l_F (см. рис. 1).
Материал стрежня – сталь Ст.3.

Требуется:

Построить эпюры продольных сил N , нормальных напряжений σ и перемещений δ .

Исходные данные:

Справочная информация:

Удельный вес стали Ст.3: γ = (77…79)×10 3 Н/м 3 .
Для расчетов принимаем удельный вес равным γ = 78×10 3 Н/м 3 .
Модуль продольной упругости (модуль Юнга) для стали Ст.3: Е = 2×10 11 Н/м 2 .

Указания:

Собственный вес стержня можно представить в виде распределенной нагрузки q₁ = γ×А₁ .
Ось z , направление силы F и нумерацию участков вести от опоры.

Решение задачи:

1. Вычерчиваем схему стержня в соответствии с исходными данными.

2. Расчет ведем от свободного конца стержня, т. е. с III-го участка.
Рассекаем стержень на силовом участке и отбрасываем часть стержня, содержащую опору (верхнюю часть).
Составляем уравнения для нахождения продольной силы N , нормального напряжения σ и удлинения стержня ∆l на силовом участке III:

2.1. Поскольку сила F на участке III не действует, то продольная сила на этом участке представлена только весом стержня, который увеличивается по мере удаления от плоскости 3-3. При этом зависимость величины продольной силы F от координаты z₃ будет прямо пропорциональной, поскольку изменяется только координата, а площадь сечения А₃ и плотность стали γ остается неизменной по всему участку.
Уравнение для продольной силы на участке:

где
q₃ – вес стержня, представленный в виде распределенной нагрузки (Н/м);
z₃ – координата рассматриваемого сечения стержня по оси z (м);
А₃ – площадь сечения участка III (м 2 );
γ – удельный вес материала стержня (для стали Ст.3 - γ = 78×10 3 Н/м 3 ).

Тогда в сечении 3-3 продольная сила будет равна нулю (т. к. и координата и вес равны нулю), а в сечении 2-2 (верхнем сечении участка III) продольная сила определится по формуле:

2.2. Нормальное напряжение на силовом участке III определяем, как отношение продольной силы к площади участка в каждом рассматриваемом сечении стержня:

Тогда в сечении 3-3 нормальное напряжение будет равно нулю (т. к. продольная сила равна нулю), а в сечении 2-2 (со стороны участка III) определится по формуле:

2.3. Удлинение бруса на участке III определяем по закону Гука, с учетом изменяющегося по координате z веса стержня:

где Е – модуль продольной упругости стали; Е = 2×10 11 Н/м 2 .

Удлинение изменяется по линейной зависимости от нижнего сечения (3-3) до верхнего сечения (2-2) участка, при этом в сечении 3-3 оно будет равно нулю, поскольку продольная сила N₃ в этом сечении равна нулю, а в сечении 2-2 удлинение будет равно:

= 78×10 3 ×0,81)/(2×2×10 11 ) ≈ 0,000000158 м или ∆l3 ≈ 0,000158 мм.

3. Проводим расчет продольных сил, нормальных напряжений и удлинений стержня на участках II и I, учитывая, что к сечению 2-2 участка II приложена продольная сила F , которая по отношению к участкам II и I является растягивающей (т. е. положительной).

3.1. Продольная сила на участках II и I будет равна:

В начале участка II:

N₂ 1 = F + N₃ = 70000 + 175,5 = 70175,5 Н или N₂ 1 ≈ 70,175 кН.

В конце участка II и в начале участка I:

= 70175,5 + (1,0×78×10 3 ×20×10 -4 ) =70331,5 Н или N₂ 2 = N₁ 1 ≈ 70,33 кН.

В конце участка I:

3.2. Нормальное напряжение на участках II и I:

В начале участка II: σ₂ 1 = N₁ 2 /А₂ = 70175/20×10 -4 = 35087500 Па или σ₂ 1 ≈ 35,09 МПа.

В конце участка II: σ₂ 2 = N₂ 2 /А₂ = 70331,5 /20×10 -4 = 35 165 750 Па или σ₂ 2 ≈ 35,16 МПа.

В начале участка I: σ₁ 1 = N₁ 1 /А₁ = 70331,5 /40×10 -4 = 17 582 875 Па или σ₁ 1 ≈ 17,58 МПа.

В конце участка I: σ₁ 2 = N₁ 2 /А₁ = 70674,7 /40×10 -4 = 17668675 Па или σ₁ 2 ≈ 17,7 МПа.

3.3. Удлинение стержня на участках II и I:

= 78×10 3 ×1)/(2×2×10 11 ) + (70156×1/2×10 11 ×20×10 -4 ) ≈ 0,00017851 м или ∆l₂ ≈ 0,1785 мм.

= (78×10 3 ×1,21)/(2×2×10 11 ) + (70343×1,1/2×10 11 ×40×10 -4 ) ≈ 0,0000991 м или ∆l₁ ≈ 0,0991 мм.

4. Определяем перемещения сечений стержня:

5. Результаты расчетов сводим в Таблицу 1, и строим эпюры продольных сил, нормальных напряжений и перемещений ( см. рис. 1 ).

Таблица 1. Значения продольной силы, нормального напряжения и удлинения стержня по сечениям силовых участков.

Как и в предыдущей статье, на этой странице приведены основные принципы решения задач технической механики на примере простейших заданий, в которых необходимо определить какие-либо силовые факторы, возникающие в конструкциях и телах напряжения, построить эпюры и т. п. Сопротивление материалов является базовой основой для решения вопросов наиболее практического раздела технической механики - "Детали машин".

Решение задачи на растяжение и сжатие

Построить эпюру напряжений в ступенчатом круглом брусе, нагруженном продольными силами и указать на наиболее напряженный участок.
Весом бруса пренебречь.

Силы:
F₁ = 100 кН;
F₂ = 400 кН;
Площадь сечения бруса: А = 0,1 м 2 .

При построении эпюры напряжений используем метод сечений, рассматривая отдельные участки бруса, как самостоятельные его элементы, находящиеся в состоянии равновесия под действием реальных и условных нагрузок. При этом исследование сечений начинаем со стороны свободного конца бруса, т. е. со стороны, где приложены известные нам силы.
Сначала разбиваем весь брус на однородные участки, границами которых служат точки приложения силовых факторов и (или) изменение размеров сечения. Для нашего бруса можно выделить три таких однородных участка - I, II, III (см. схему 2) .

Для каждого из участков определяем нормальные напряжения в сечениях по формуле σ = F/A , где: F - величина продольной силы в сечении, А - площадь сечения. При этом следует учитывать знаки: если сила растягивающая, то ее условно считают положительной, если сжимающая - отрицательной. Соответственно, напряжения будут иметь такие же знаки, как и силы.

После подсчетов получим:
σ_I = F₁/A = - 100×10 3 /0,1 = -1000000 Па (-1 МПа),
σ_II = F₁/2A = - 100×10 3 /2×0,1 = -500000 Па (-0,5 МПа),
σ_III = (F₂ - F₁)/A = (400 - 100)×10 3 /0,1 = 3000000 Па (3 МПа).

Построение эпюры напряжений начинаем с проведения линии, параллельной оси бруса (эта линия условно изображает брус и является нулевой ординатой графика эпюры) . Затем, начиная от свободного конца бруса, откладываем от линии, как от нулевой ординаты, величины напряжений по каждому участку с учетом их знаков.
На брусе, приведенном в задании, величина напряжений в каждом сечении отдельных участков будет одинакова, и лишь в граничных (расположенных между соседними участками) сечениях появится скачок напряжения в виде ступени (здесь используется принцип Сен-Венана, условно полагающий, что в месте приложения нагрузки напряжение изменяется скачкообразно) .

Построение эпюры завершается указанием на ее площадках знаков напряжения в кружках, проведением тонких линий перпендикулярно оси (нулевой ординаты) эпюры (эти линии условно изображают сечения бруса) и расстановкой величины напряжений на внешних углах графика (на внутренних углах цифровые обозначения не наносятся) . Слева от эпюры указывается, что на ней изображено (в нашем случае - Эпюра σ )

В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок. Для бруса, представленного в задаче, максимальные напряжения возникают в сечениях участка III (см. схему) . Поскольку эти напряжения положительны, они являются растягивающими

Решение задачи с использованием закона Гука

Определить величину растягивающей силы F , если известно, что под ее действием брус удлинился на величину ΔL .

Удлинение бруса ΔL = 0,005 мм;
Модуль продольной упругости балки Е = 2,0×10 5 МПа;
Площадь сечения бруса A = 0,01 м 2 ;
Размеры бруса и точка приложения силы F приведены на схеме.

Решить задачу можно, используя известную зависимость между линейными удлинениями и нагрузками (закон Гука).
Согласно закону Гука, представленному в расширенном виде:

ΔL = FL/(EA) , откуда: F = (ΔLEA)/L .

Поскольку сила F приложена не к крайнему сечению бруса, а к его середине, то удлинился лишь участок между жесткой заделкой и сечением, к которому приложена растягивающая сила, имеющий длину L₁ = 2 м.
Учитывая это, определяем силу, вызвавшую удлинение бруса (не забываем привести все величины к единицам системы СИ):

F = (ΔLEA)/L₁ = (0,005×10 -3 ×2×10 11 ×0,01)/2 = 5000 Н = 5,0 кН .

Решение задачи на срез и смятие

Венец зубчатого колеса прикреплен к ступице болтовыми соединениями из шести болтов с гайками, размещенными равномерно по окружности диаметром D .
Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.

Номинальный крутящий момент на валу шестерни: Мкр = 10 Нм;
Диаметр окружности, на которой размещены болтовые соединения D = 0,4 м;
Диаметр стержня болта d = 10 мм.

Для решения задачи воспользуемся зависимостью между напряжением среза, внешней нагрузкой и площадью сечения по плоскости среза:

где: τ_ср - касательное напряжение среза, F_окр - окружная сила на расстоянии от оси вращения до центра болта, A - площадь сечения (в нашем случае - площадь поперечного сечения 6 болтов) .

Окружную силу можно определить, зная крутящий (вращающий) момент на валу зубчатого колеса и расстояние от оси вращения зубчатого колеса до центра болта:
F_окр = 2Мкр/D.
Площадь сечения одного болта: А(1) = πd 2 /4, шести болтов: А = 3πd 2 /2 .
Подставив эти значения в исходную формулу, определим касательное напряжение сдвига (среза) болта:

τ_ср = F_окр /A = (2Мкр/D) / (3πd 2 /2) = (2×10/0,4) / (3×3,14 0,01 2 /2) ≈ 106 000 Па (или 0,106 МПа) .

Решение задачи на срез и смятие шпонки

Произвести проверочный расчет призматической шпонки на смятие.

Вращающий момент на валу Т = 120 Нм;
Радиус сечения вала r = 30 мм;
Высота шпонки h = 6 мм;
Рабочая длина шпонки l_р = 30 мм;
Допускаемое напряжение на смятие [σ]_см = 200 МПа

Решение задачи сводится к определению напряжения смятия, возникающего в продольном сечении шпонки, выступающем над канавкой вала (рабочая площадь шпонки) . Это напряжение можно определить из формулы:

где: σ_см - искомое напряжение смятия,
F_окр - окружная сила, действующая на рабочую поверхность шпонки: F_окр = Т/r.

Учитывая, что высота рабочей поверхности шпонки невелика, можно принять для расчета напряжения окружную силу, действующую на расстоянии r от оси вращения вала (радиус вала). Если необходимо выполнить более точный расчет, следует к радиусу вала прибавить половину высоты рабочей поверхности шпонки (в нашем случае - h/4).

A_раб - площадь шпонки, подвергаемая смятию: A_раб = hl_р /2 (здесь l_р - рабочая длина шпонки) .

Подставив полученные значения окружной силы и площади шпонки, работающей на смятие, в формулу (1) , получим:

σ_см = F_окр /A_раб = (Т/r) / (hl_р /2) = (120/0,03) / (0,003×0,03/2) = 88 900 000 Па (или 88,9 МПа) .

Полученное напряжение сравниваем с допускаемым напряжением смятия [σ_см] = 200 МПа, и делаем вывод, что шпонка выдержит нагрузку.

Решение задачи на кручение

Построить эпюру вращающих моментов для круглого однородного бруса, представленного на схеме. Указать наиболее нагруженный участок бруса и определить напряжение в его сечениях.

Вращающие моменты:
Т₁ = 150 Нм;
Т₂ = 400 Нм;
Т₃ = 50 Нм;
Диаметр бруса d = 0,05 м.

Построение эпюр вращающих (крутящих моментов) начинаем со стороны свободного конца бруса, откладывая величины крутящих моментов от оси абсцисс (нулевой ординаты) бруса с соблюдением знаков моментов (см. схему) .

Из эпюры очевидно, что максимальный крутящий момент возникает в сечениях участка I: Мкр = 500 Нм. Для определения напряжения (при кручении возникает касательное напряжение), воспользуемся зависимостью, полученной ранее:

где: W_r ≈ 0,2d 3 - момент сопротивления круглого сечения кручению (или полярный момент сопротивления круглого сечения).

Подставив полученные зависимости и их числовые значения в формулу, получим максимальное напряжение τ_max , возникающее в сечениях участка I при кручении бруса:

τ_max ≈ М_кр / 0,2d 3 ≈ 500/0,2×0,05 3 ≈ 200 000 000 Па (или 200 МПа).

С правилами и примерами построения эпюр при деформации кручения можно ознакомиться здесь.

Решение задачи на изгиб

Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F .
Вес бруса не учитывать.

Исходные данные:

Поперечная сила F = 1000 Н;
Длина бруса L = 5 м;
Диаметр бруса d = 0,1 м.

Изгибающий момент силы F и возникающие в сечениях бруса напряжения зависят от расстояния между линией приложения (вектором) силы и плоскостью рассматриваемого сечения (очевидно, что величина изгибающего момента находится в прямо пропорциональной зависимости от расстояния до вектора силы) . Поэтому для данного бруса изгибающий момент достигает максимального значения в сечении рядом с жесткой заделкой:

Ми_max = FL = 1000×5 = 5000 Нм.

Максимальные нормальные напряжения в этом сечении можно определить по формуле:

где: W ≈ 0,1d 3 - момент сопротивления круглого сечения изгибу (или осевой момент сопротивления круглого сечения). Подставив зависимости и их величины в формулу, получим:

σ_max ≈ Ми_max / 0,1d 3 ≈ 5000/0,1х0,1 3 ≈ 50 000 000 Па (или 50 МПа).

Решение задачи на изгиб с построением эпюр

Построить эпюру поперечных сил и изгибающих моментов, действующих на защемленный одним концом брус (см. схему).

Поперечная сила F = 50 Н;
Распределенная нагрузка q = 10 Н/м;
Длина бруса L = 12 м;
Вес бруса не учитывать.

Для построения эпюр определим границы участков бруса, в пределах которых внешние нагрузки и размеры сечений одинаковы. Для данного бруса можно выделить два таких участка (см. схему) .

Далее, используя метод сечений, строим эпюру поперечных сил, учитывая знаки. Очевидно, что на первом участке поперечная сила будет постоянной во всех сечениях, и эпюра представляет собой горизонтальную линию, отстоящую от оси эпюры на величину -F (сила отрицательная).

В среднем сечении бруса начинает действовать распределенная нагрузка, которая линейно увеличивается и суммируется с поперечной силой F в каждом последующем сечении бруса по направлению к жесткой заделке. Поскольку эпюра поперечных сил на втором участке представляет собой отрезок наклонной прямой, то для ее построения достаточно определить величину поперечной силы в середине бруса (очевидно, что здесь F = 50 Н) и величину поперечной силы в сечении рядом с жесткой заделкой:
F₂ = -FL - 6q = -50 - 10×6 = -110 Н.
По полученным значениям строим эпюру поперечных сил F (см. схему) .

Построение эпюры изгибающих моментов строится аналогично эпюре поперечных сил - при помощи метода сечений. При этом учитывается расстояние от сечения, в котором приложена поперечная сила, до рассматриваемого сечения (плечо силы).
Очевидно, что изгибающий момент от силы F будет увеличиваться прямо пропорционально по мере удаления от сечения, к которому она приложена, причем в крайнем сечении (где приложена сила) момент этой силы равен нулю (поскольку плечо силы равно нулю) .
В среднем сечении бруса изгибающий момент достигает значения: Ми = FL/2 = -50×6 = -300 Нм .

Начиная с середины бруса начинает действовать изгибающий момент от распределенной нагрузки q, который в каждом сечении определяется, как произведение приведенной силы F_пр = ql на половину расстояния l (здесь l - расстояние от рассматриваемого сечения до начала действия распределенной нагрузки) .
Очевидно, что по мере удаления от среднего сечения к жесткой заделке изгибающий момент от распределенной нагрузки q изменяется по квадратичной зависимости, и линия эпюры изгибающих моментов на втором участке представляет собой параболу.

Чтобы построить параболу недостаточно двух точек, необходимо определить величину изгибающего момента в нескольких сечениях бруса (на втором участке) . При этом следует учитывать изгибающий момент от силы F, который суммируется с изгибающим моментом от распределенной нагрузки q на данном участке бруса.
Максимальной величины изгибающий момент достигает в сечении рядом с жесткой заделкой:

Ми_max = - FL + [-q×(L/2)×(L/4)] = -50×12 + [-10×(12/2)×(12/4)] = -780 Нм.

Выполнив необходимые подсчеты, строим эпюру изгибающих моментов, начиная со свободного конца бруса (см. схему) .

Ознакомиться с примером построения эпюр продольных сил, напряжений и перемещений.

Задача 1.Двухступенчатый стальной брус нагружен силами F₁=30 кН F₂=40 кН.

Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А₁=1,5см 2 ;А ₂=2см 2 .

Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.

Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Разбиваем брус на участки.

Определяем ординаты эпюры N на участках бруса:

Строим эпюру продольных сил

Вычисляем ординаты эпюры нормальных напряжений

σ₁ = = –200МПа

σ₂ = = –150МПа

σ ₃= =50МПа

Строим эпюры нормальных напряжений.

4. Проверяем прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Выбираем максимальное по модулю расчетное напряжение. Iσ_maxI = 200 МПа

Подставляем в условие прочности Iσ_maxI ≤ [σ]

200 МПа ≤ 160 МПа. Делаем вывод, что прочность не обеспечена.

5. Определяем перемещение свободного конца бруса Е = 2∙10 5 МПа.

∆l=∆l₁+∆l₂+∆l₃

∆l₁= = – 0,5мм

∆l₂= = – 0,225мм

∆l₃= = 0,05мм

∆l= - 0,5 – 0,225 + 0,05 = – 0,675мм

Брус укоротился на 0,675мм

1. Задание: Решить задачи

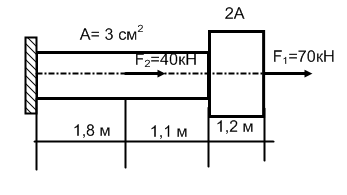
Двухступенчатый стальной брус нагружен силами F₁, F₂.

Разбить брус на участки. Пронумеровать эти участки.

Найти величину продольной силы на первом участке.

Найти величину продольной силы на втором участке.

Найти величину продольной силы на третьем участке.

Построить эпюру для продольной силы.

Найти величину нормального напряжения на первом участке.

Найти величину нормального напряжения на втором участке.

Найти величину нормального напряжения на третьем участке.

Построить эпюру для нормального напряжения.

Проверить прочность бруса. Допускаемое напряжение [σ] = 160 МПа.

Определить перемещение свободного конца бруса.

Задание 2

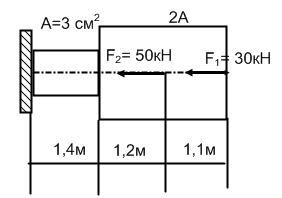
Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Задание 3

Литература
В.П. Олофинская «Техническая механика» курс лекций с вариантами практических и тестовых заданий.
Лекции по теме (конспекты).

Тема 2.2. Растяжение и сжатие. Продольные и поперечные деформации. Закон Гука

Иметь представление о продольных и поперечных деформациях и их связи.

Знать закон Гука, зависимости и формулы для расчета напряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость статически определимых брусьев при растяжении и сжатии.

Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).

В сопротивлении материалов принято рассчитывать деформации в относительных единицах:

Между продольной и поперечной деформациями существует зависимость

где μ— коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.

Закон Гука

В пределах упругих деформаций деформации прямо пропорциональны нагрузке:

где F — действующая нагрузка; к — коэффициент. В современной форме:

Е — модуль упругости, характеризует жесткость материала.

В пределах упругости нормальные напряжения пропорциональны относительному удлинению.

Значение Е для сталей в пределах (2 – 2,1) • 10 5 МПа. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:

Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии

Используем известные формулы.

В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:

Δl — абсолютное удлинение, мм;

σ — нормальное напряжение, МПа;

l — начальная длина, мм;

Е — модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь поперечного сечения, мм 2 ;

Произведение АЕ называют жесткостью сечения.

Выводы

1. Абсолютное удлинение бруса прямо пропорционально величине продольной силы в сечении, длине бруса и обратно пропорционально площади поперечного сечения и модулю упругости.

2. Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом Пуассона, называемом коэффициентом поперечной деформации.

Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.

3. Поперечные деформации меньше продольных и редко влияют на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.

где Δа — поперечное сужение, мм;

а_о — начальный поперечный размер, мм.

4. Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях на растяжение по диаграмме растяжения (рис. 21.2).

При работе пластические деформации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.

На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.

Примеры решения задач

Пример 1. Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, определить перемещение свободного конца.

Решение

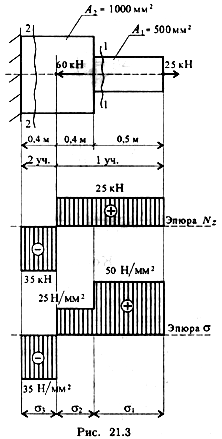
1. Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных напряжений.

Делим брус на участки нагружения, определяем продольные силы, строим эпюру продольных сил.

2. Определяем величины нормальных напряжений по сечениям с учетом изменений площади поперечного сечения.

Строим эпюру нормальных напряжений.

3. На каждом участке определяем абсолютное удлинение. Результаты алгебраически суммируем.

Примечание. Балка защемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчет начинаем со свободного конца (справа).

1. Два участка нагружения:

Три участка по напряжениям:

Пример 2. Для заданного ступенчатого бруса (рис. 2.9, а) построить эпюры продольных сил и нормальных напряжений по его длине, а также определить перемещения свободного конца и сечения С, где приложена сила Р₂. Модуль продольной упругости материала Е = 2,1 • 10 5 Н/'мм 3 .

1. Заданный брус имеет пять участков /, //, III, IV, V (рис. 2.9, а). Эпюра продольных сил показана на рис. 2.9, б.

2. Вычислим напряжения в поперечных сечениях каждого участка:

Эпюра нормальных напряжений построена на рис. 2.9, в.

3. Перейдем к определению перемещений поперечных сечений. Перемещение свободного конца бруса определяется как алгебраическая сумма удлинений (укорочений) всех его участков:

Подставляя числовые значения, получаем

4. Перемещение сечения С, в котором приложена сила Р₂, определяется как алгебраическая сумма удлинений (укорочений) участков ///, IV, V:

Подставляя значения из предыдущего расчета, получаем

Таким образом, свободный правый конец бруса перемещается вправо, а сечение, где приложена сила Р₂, — влево.

5. Вычисленные выше значения перемещений можно получить и другим путем, пользуясь принципом независимости действия сил, т. е. определяя перемещения от действия каждой из сил Р₁; Р_2; Р₃ в отдельности и суммируя результаты. Рекомендуем учащемуся проделать это самостоятельно.

Пример 3. Определить, какое напряжение возникает в стальном стержне длиной l = 200 мм, если после приложения к нему растягивающих сил его длина стала l₁ = 200,2 мм. Е = 2,1*10 6 Н/мм 2 .

Абсолютное удлинение стержня

Продольная деформация стержня

Согласно закону Гука

Пример 4. Стенной кронштейн (рис. 2.10, а) состоит из стальной тяги АВ и деревянного подкоса ВС. Площадь поперечного сечения тяги F₁ = 1 см 2 , площадь сечения подкоса F₂ = 25 см 2 . Определить горизонтальное и вертикальное перемещения точки В, если в ней подвешен груз Q = 20 кН. Модули продольной упругости стали E_ст = 2,1*10 5 Н/мм 2 , дерева Е_д = 1,0*10 4 Н/мм 2 .

1. Для определения продольных усилий в стержнях АВ и ВС вырезаем узел В. Предполагая, что стержни АВ и ВС растянуты, направляем возникающие в них усилия N₁ и N₂ от узла (рис. 2.10, 6). Составляем уравнения равновесия:

Усилие N₂ получилось со знаком минус. Это указывает на то, что первоначальное предположение о направлении усилия неверно — фактически этот стержень сжат.

2. Вычислим удлинение стальной тяги Δl₁ и укорочение подкоса Δl₂:

Тяга АВ удлиняется на Δl₁ = 2,2 мм; подкос ВС укорачивается на Δl₁ = 7,4 мм.

3. Для определения перемещения точки В мысленно разъединим стержни в этом шарнире и отметим их новые длины. Новое положение точки В определится, если деформированные стержни АВ₁ и В₂С свести вместе путем их вращения вокруг точек А и С (рис. 2.10, в). Точки В₁ и В₂ при этом будут перемещаться по дугам, которые вследствие их малости могут быть заменены отрезками прямых В₁В' и В₂В', соответственно перпендикулярными к АВ₁ и СВ₂. Пересечение этих перпендикуляров (точка В') дает новое положение точки (шарнира) В.

4. На рис. 2.10, г диаграмма перемещений точки В изображена в более крупном масштабе.

5. Горизонтальное перемещение точки В

где составляющие отрезки определяются из рис. 2.10, г;

Подставляя числовые значения, окончательно получаем

При вычислении перемещений в формулы подставляются абсолютные значения удлинений (укорочений) стержней.

Контрольные вопросы и задания

1. Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (μ = 0,25.)

2. Что характеризует коэффициент поперечной деформации?

3. Сформулируйте закон Гука в современной форме при растяжении и сжатии.

4. Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?

5. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

6. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

7. Ответьте на вопросы тестового задания.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.

Читайте также: