Подобрать сечение балки из стального двутавра

Обновлено: 25.04.2024

Перед началом расчета стальной балки необходимо собрать нагрузку, действующая на металлическую балку. В зависимости от продолжительности действия нагрузки разделяют на постоянные и временные.

К постоянным нагрузкам относятся:

собственный вес металлической балки;
собственный вес перекрытия и т.д.;

К временным нагрузкам относятся:

длительная нагрузка (полезная нагрузка, принимается в зависимости от назначения здания);
кратковременная нагрузка (снеговая нагрузка, принимается в зависимости от географического расположения здания);
особая нагрузка (сейсмическая, взрывная и т.д. В рамках данного калькулятора не учитывается);

Нагрузки на балку разделяют на два типа: расчетные и нормативные. Расчетные нагрузки применяются для расчета балки на прочность и устойчивость (1 предельное состояние). Нормативные нагрузки устанавливаются нормами и применяется для расчета балки на прогиб (2 предельное состояние). Расчетные нагрузки определяют умножением нормативной нагрузки на коэффициент нагрузки по надежности. В рамках данного калькулятора расчетная нагрузка применяется при определении прогиба балки в запас.

Нагрузки можно собрать на нашем сайте.

После того как собрали поверхностную нагрузку на перекрытие, измеряемой в кг/м2, необходимо посчитать сколько из этой поверхностной нагрузки на себя берет балка. Для этого надо поверхностную нагрузку умножить на шаг балок(так называемая грузовая полоса).

Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 500кг/м2, а шаг балок 2,5м. Тогда распределенная нагрузка на металлическую балку будет: Qраспр.= 500кг/м2 * 2,5м = 1250кг/м. Эта нагрузка вносится в калькулятор

2. Построение эпюр

Далее производится построение эпюры моментов, поперечной силы. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.

3. Расчет по прочности и прогибу

После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и из таблицы сортамента выбрать подходящий металлопрофиль. Вертикальный предельный прогиб fult принимается по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия). Пункт2.а в зависимости от пролета. Например предельный прогиб fult=L/200 при пролете L=6м. означает, что калькулятор подберет сечение прокатного профиля (двутавра, швеллера или двух швеллеров в коробку), предельный прогиб которого не будет превышать fult=6м/200=0,03м=30мм. Для подбора металлопрофиля по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента подбирают подходящий металлопрофиль.

4. Подбор металлической балки из таблицы сортамента

Из двух результатов подбора (1 и 2 предельное состояние) выбирается металлопрофиль с большим номером сечения.

Подобрать сечение балки из стального двутавра

Чтобы посчитать сечение деревянной балки - необходимо собрать нагрузку, действующая на балку. В зависимости от длительности действия нагрузки разделяют на постоянные и временные.

собственный вес деревянной балки;
собственный вес перекрытия, чердачного перекрытия и т.д.;

Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 400кг/м2, а шаг балок 0,6м. Тогда распределенная нагрузка на деревянную балку будет: Qраспр.= 400кг/м2 * 0,6м = 240кг/м. Эта нагрузка вносится в калькулятор

2. Выбор предельного прогиба

В зависимости от назначения балки и ее пролета задаем вертикальный предельный прогиб по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия) Пункт2.а. Смысл вертикального прогиба заключается в следующем: например, прогиб l/250 означает, что для балки длинной 4м предельный вертикальны прогиб равен fult = 4м / 250 = 0,016м = 16мм в месте максимального прогиба для балки. Для балки на двух опорах загруженной равномерно или с сосредоточенной нагрузкой посередине балки - максимальный прогиб будет посередине пролета. Для консольной балки максимальный прогиб - на свободном конце балки.

3. Задание ширины искомого сечения балки.

В зависимости от конструктивных требований задаем ширину сечения балки. Расчет деревянной балки сводится к тому, что необходимо подобрать требуемую высоту hтр сечения деревянной балки, которое способно выдержать заданную нагрузку и не превысить заданный предельный прогиб.

Алгоритм расчета деревянной балки, используемый в данном калькуляторе

По заданной нагрузке и пролету производится построение эпюры моментов и поперечной силы. Эпюра поперечной силы находится для информации (чтобы знать какая нагрузка давит на опоры балки) и в расчете не используется. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.

2. Расчет по прочности и прогибу

После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и hтр и из таблицы рекомендуемого сортамента выбрать подходящее сечение высотой равное hтр деревянной балки по ширине сечения (b) и по Wтр. Следует отметить, что калькулятор подбирает именно по Wтр, нахождение hтр сделано для наглядности, чтобы видеть какая высота сечения должна быть. Для подбора деревянной балки по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента пиломатериалов подбирают подходящее сечение.

3. Подбор деревянной балки из таблицы сортамента пиломатериалов по ГОСТ 244454-80

Из двух результатов подбора (1 и 2 предельное состояние) выбирается сечение с большей выстой сечения.

Как подобрать двутавр: формулы и пример

В этой статье рассмотрим, как подобрать двутавровое поперечное сечение при плоском изгибе.

Поперечное сечение при плоском изгибе, всегда подбирается по нормальным напряжениям, так как касательные напряжения при данном виде деформации, как правило, в несколько раз меньше, за исключением тех случаев, когда поперечные силы имеют большие значения.

Условие прочности для двутавра

Условие прочности при поперечном изгибе выглядит таким образом:

В неравенстве слева записано максимальное расчётное напряжение, а справа напряжение допустимое.

Максимальное расчётное напряжение можно найти двумя способами:

Как отношение максимального изгибающего момента к моменту сопротивления:

Либо по такой формуле, с использованием момента инерции:

где М_max — максимальный изгибающий момент, y — расстояние от нейтральной линии до крайней точки сечения, J — момент инерции сечения.

Момент инерции и момент сопротивления связаны следующим образом:

Какую формулу удобнее использовать?

Если в условии задачи вас просят найти максимальное напряжение, то используйте формулу с моментом сопротивления. То есть, по этой формуле вы сразу вычислите максимальные напряжения в крайних точках сечения.
Если вам потребуется найти напряжение в любой другой точке сечения, например, в месте перехода полки в стенку, то используйте вторую формулу.

Подбор двутавра на практике

Ну что же, самое время перейти к практике. Например, посчитали вы балку, построили эпюры и нужно теперь подобрать двутавр удовлетворяющий условию прочности. Для этого вам необходимо:

Проанализировать эпюру изгибающих моментов и определить положение наиболее опасного сечения. Опасным можно считать то сечение, в котором изгибающий момент максимален. Скажем, у вас он будет равен 30 кНм.

Далее необходимо определить минимально допустимый момент сопротивления из условия прочности. Допустимое напряжение примем равным 160 МПа:

Нашли момент сопротивления. Далее по сортаменту двутавров (ГОСТ 8239-89) выбираем номер профиля, у которого момент сопротивления будет ближайшим большим к нашему расчётному. Это двутавр № 20а у которого момент сопротивления равен 203 см 3 .

Делаем проверочный расчет. Вычисляем напряжение с табличным значением момента сопротивления:

Так как получили напряжение меньшее, чем допустимое, можно сделать вывод, что подобранный двутавр удовлетворяет условию прочности.

Сортамент двутавров в виде таблиц

На этой странице размещен сортамент двутавров с основными характеристиками профилей. Все характеристики двутавров представлены в виде таблиц. Кроме того, на этой страничке расскажем немного информации о самих двутаврах: как они обозначаются, какие материалы используются для их производства и где применяются.

Таблицы двутавров

В этом блоке статьи расскажем о возможностях таблиц двутавров на нашем сайте и как с ними взаимодействовать.

Выборка нужной информации в таблице

Каждая таблица снабжена удобным фильтром, позволяющим делать выборку нужных данных. Как пользоваться фильтром? Например, вам нужно подобрать балку с двутавровым поперечным сечением. Вы рассчитали минимально допустимый момент сопротивления из условия прочности, выбрали в табличке ближайший больший момент сопротивления и вам нужно переписать другие характеристики двутавра с подходящим моментом сопротивления.

Вбиваете численное значение момента сопротивления в поиск, и фильтр покажет только характеристики подобранного профиля, а остальные отбросит.

Вывод строчек сортамента

У каждой таблицы выведено ТОЛЬКО 10 строчек, для удобства просмотра сортамента. Между строчками можно переключаться, с помощью кнопок под каждой таблицей:

В последнем обновлении сайта, таблицы двутавров были обновлены. Теперь они адаптивны к любым типам устройств, с различными размерами экрана. Содержимое таблиц подстраивается под ваше устройство. Для мобильных устройств, имеющих маленькое разрешение экрана, внизу каждой таблички появляется горизонтальная прокрутка.

Вот и всё, что хотелось бы рассказать по функционалу таблиц. Надеемся, вам понравится пользоваться сортаментом! Чуть ниже в статье расскажем о двутаврах, их применении и используемых обозначениях. В самом низу статьи можете найти сами таблицы двутавров.

О двутаврах

Что такое двутавр? Это профильное изделие, которое изготавливают из разного типа сталей, для их производства применяют методы горячего проката. Кроме этого, двутавровая балка может быть изготовлена из дерева или из полимерных материалов. Отличительной чертой от других типов балок является то, что в сечении оно напоминает букву Н.

Основная сфера применения двутавровых стальных балок — это строительная отрасль, возведение мостовых конструкций и т.д. В строительстве жилых и промышленных зданий их используют для сооружения потолочных перекрытий.

Применяемость двутавровых балок

Бурное развитие строительной отрасли и машиностроения привело к необходимости роста объемов производства двутавровых балок. В наши дни, двутавр применяют и в малоэтажном строительстве, в масштабных проектах по сооружению промышленных и коммерческих зданий. В результате многочисленных исследований было доказано, что балки с Н-образным сечением эффективно использовать для:

балок перекрытий;
в конструкциях железнодорожных вагонов;
автомобилей, в частности, грузовиков;
специальной техники — экскаваторов.

Кроме того, с их помощью воздвигают арочные и модульные конструкции, которые используют в торговых и промышленных корпусах.

Полный расчет балки на прочность и жесткость

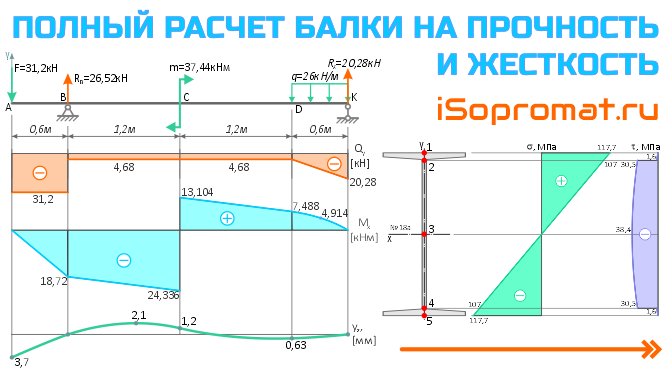
Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки при заданной системе внешних изгибающих нагрузок.

Задача

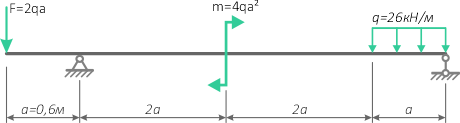
Выполнить полный расчёт на прочность и проверить жёсткость стальной, двутавровой, статически определимой балки на двух опорах

при следующих данных:
Интенсивность равномерно распределенной нагрузки q=26кН/м, продольный размер a=0,6м, сосредоточенная сила F=2qa, изгибающий момент m=4qa 2 .
Допускаемые нормальные напряжения [σ]=160МПа,
Модуль упругости I рода Е=200ГПа.
Допустимый прогиб балки [f]=l/400.

Последовательность решения задачи
Для расчета балки на прочность

Вычерчивается схема нагружения в масштабе, с указанием числовых значений приложенных нагрузок;
Строятся эпюры внутренних силовых факторов Q_y и M_x;
По условию прочности подбирается двутавровое сечение (№ двутавра) стальной балки:
Для балки двутаврового профиля выполняется полная проверка на прочность, приняв
Проверяется прочность по главным напряжениям в опасных точках сечения по III гипотезе прочности
По результатам расчетов дается заключение о прочности балки при выбранном сечении.
В случае невыполнения условия прочности по главным напряжениям, подбирается новый номер двутавра.

Для расчета балки на жесткость

С использованием универсальных уравнений метода начальных параметров (МНП) определяются углы поворота θ над опорами и прогибы в характерных сечениях (2-3 сечения), а также, максимальные прогибы балки в пролете и консольной части;
По этим данным, в соответствии с эпюрой M_x, строится линия изогнутой оси балки;
Проверяется выполнение условия жесткости балки.
Если условие жесткости не удовлетворяется, подбирается новое двутавровое сечение, обеспечивающее необходимую жесткость.

Решение

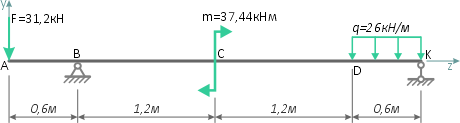
Рассчитаем численные значения силы F и момента m, которые были заданы в виде переменных.
Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.

Показываем оси системы координат y-z и обозначаем характерные сечения балки.

Полный расчет стальной балки на прочность

Определение реакций в шарнирных опорах балки

Направим реакции опор вверх и запишем суммы моментов относительно точек на опорах, нагрузок приложенных к балке

Из составленных уравнений выражаем и находим реакции.
Из первого уравнения
из второго
Положительные значения указывают на то, что произвольно заданное направление реакций вверх оказалось верным.

Выполним проверку найденных реакций опор спроецировав все силы на ось y
Равенство суммы проекций сил нулю говорит о том что реакции опор определены правильно.

Более подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

Построение эпюр внутренних силовых факторов

Рассчитаем значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.

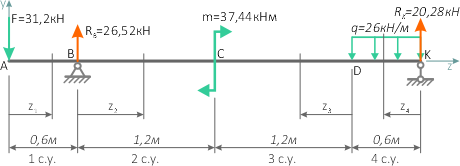
Балка имеет 4 силовых участка.

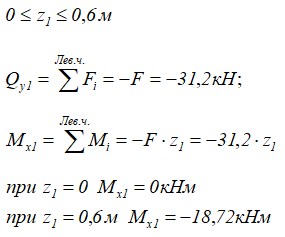
1 участок (AB)

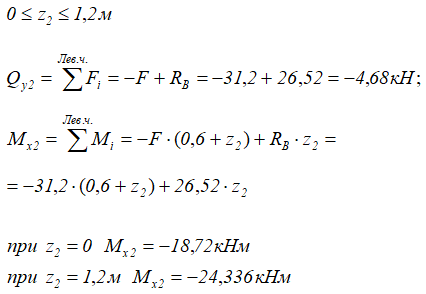
2 участок (BC)

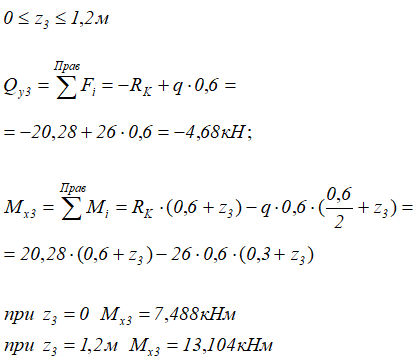
3 участок (CD)

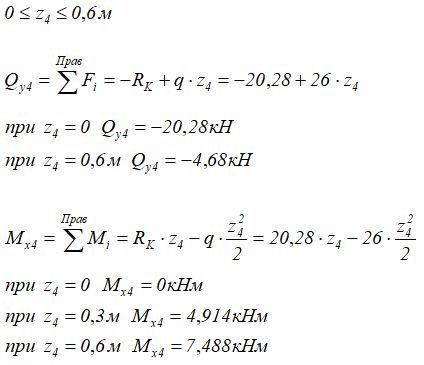
4 участок (DK)

Здесь, значения Q_y на границах участка имеют одинаковый знак, поэтому на этом участке, на эпюре M_x экстремума не будет.

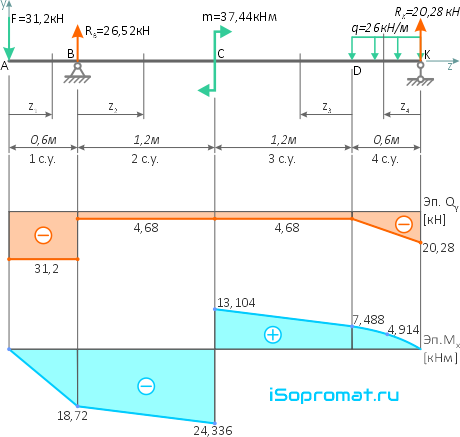
По полученным данным строим эпюры внутренних поперечных сил Q_y и изгибающих моментов M_x.

Проверка построенных эпюр:
— по дифференциальным зависимостям
— в сечениях балки, где приложены сосредоточенные силы, на эпюре Q_y имеются скачки значений на величину соответствующей силы;
— в сечениях балки, где приложены изгибающие моменты, на эпюре M_x скачки значений на величину соответствующего момента.
Все условия выполнены, следовательно, эпюры построены верно.

По эпюрам видно, что опасным является сечение балки в точке C, где:
M_x=M_{x max}=-24,336кНм
Q_y=-4,68кН

Подбор двутаврового сечения балки

Подберем двутаврового сечение балки по условию прочности по нормальным напряжениям
где
M_{x max} – максимальное значение внутреннего изгибающего момента в сечениях балки. Принимается с построенной эпюры M_x;
W_x – осевой момент сопротивления поперечного сечения балки относительно горизонтальной оси x;
[σ] – допустимые нормальные напряжения.

Выразим и рассчитаем минимально необходимое значение осевого момента сопротивления поперечного сечения балки W_x обеспечивающего её прочность по нормальным напряжениям
По сортаменту прокатной стали выбираем номер двутавра имеющий осевой момент сопротивления близкий к расчетному W_x=152,1см 3 в большую сторону.

Это двутавр №18а у которого W_x=159,0см 3 .

Максимальные нормальные напряжения в сечении

Этот двутавр будет работать при максимальных нормальных напряжениях в крайних слоях опасного сечения балки.

Максимальные нормальные напряжения выбранного номера двутавра не превышают допустимых значений, значит сечение подобрано верно.

Полная проверка на прочность двутаврового сечения

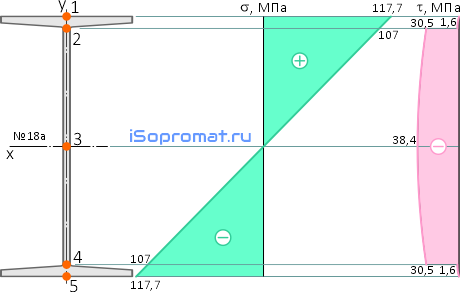
При изгибе тонкостенных прокатных профилей, таких как, например, двутавр или швеллер, в местах соединения стенки с полкой нормальные и касательные напряжения имеют не максимальные, но достаточно большие значения.

Их совместное действие, выраженное в виде главных (эквивалентных) напряжений, может превышать допустимые значения, что будет означать потерю прочности в этих точках поперечного сечения балки.

В отношении главных напряжений неблагоприятным является сечение балки B, в котором максимально значение поперечной силы при значительном изгибающем моменте:

Для полной проверки на прочность построим эпюры нормальных и касательных напряжений в сечении B для выбранного номера двутавра.

Построение эпюр нормальных и касательных напряжений в сечении балки подробно рассмотрено здесь:

Для выполнения расчетов, из сортамента выпишем необходимые геометрические характеристики выбранного номера двутавра:
Высота сечения
h=180мм;
Ширина сечения
b=100мм;
Толщина стенки
d=5,1мм;
Толщина полки
t=8,3мм;
Осевой момент инерции поперечного сечения
I_x=1430см 4 ;
Статический момент сечения
S_x=89,8см 3 .

Двутавровое сечение по высоте имеет 5 характерных точек: верхнюю (1), нижнюю (5), среднюю (3) и две точки в местах перехода стенки в полку двутавра (2 и 4).

Для построения эпюр, определим значения напряжений в указанных точках сечения.

Нормальные напряжения в сечении балки распределяются по линейному закону, поэтому для построения эпюры достаточно найти максимальные значения
Касательные напряжения в характерных точках сечения рассчитываются по формуле Журавского
где
Q_y — поперечная сила в данном сечении. Принимается с эпюры с учетом знака;
I_x – осевой момент инерции поперечного сечения;
b_y – ширина сечения на уровне рассматриваемой точки;
S_x* — статический момент части сечения, расположенной между уровнем рассматриваемой точки и верхним (нижним) краем сечения.

Рассчитаем значения касательных напряжений

Так как выше точки 1 и ниже точки 5 площадь сечения равна нулю, то статический момент S_x* для этих точек тоже равен нулю, следовательно
В точке 3

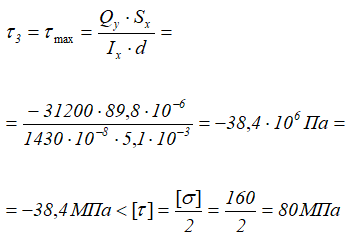
В точке 3 будут максимальные касательные напряжения, т.к. для неё статический момент сечения S_x максимальный при минимальной ширине сечения d

Видно, что прочность сечения по касательным напряжениям обеспечена.

В точках, где стенка двутавра переходит в полку, будут скачки напряжений, так как на уровне этих точек резко меняется ширина сечения

Рассчитаем значения напряжений в этих точках для стенки (с) и полки (п)

Статический момент полки двутавра
Касательные напряжения в точках 2 и 4 полки
Касательные напряжения в точках 2 и 4 стенки
По этим данным строим эпюры нормальных и касательных напряжений для выбранного номера двутавра.

Рассчитаем величину главных напряжений в точках соединения полки со стенкой двутавра (т. 2 и 4)

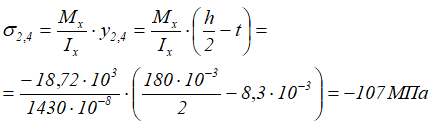
Нормальные напряжения в рассматриваемых точках

Эквивалентные напряжения в опасных точках сечения
Как видно, величина эквивалентных напряжений не превышает допустимых значений, следовательно, выбранный номер двутавра удовлетворяет условию прочности и по главным напряжениям.

Полный расчет балки на жесткость

Для того чтобы балка удовлетворяла условию жесткости, линейные перемещения (прогибы) балки y_z не должны превышать заданных допустимых значений [f], т.е. должно выполняться условие жесткости

Расчет перемещений сечений балки

Расчет перемещений сечений балки выполним методом начальных параметров (МНП).

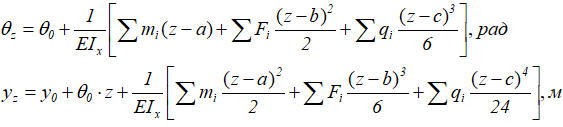
Шаблоны уравнений метода начальных параметров имеют вид:

Здесь:
θ_z — угловое перемещение (угол наклона) рассматриваемого сечения;
y_z — вертикальное линейное перемещение (прогиб) рассматриваемого сечения балки;
z – расстояние от выбранного начала координат балки до рассматриваемого сечения (координата);
θ₀, y₀ — соответственно угловое и линейное перемещения балки в выбранном начале координат (начальные параметры);
E – модуль упругости I рода для материала балки;
I_x – осевой момент инерции сечения балки;
m, F, q – соответственно моменты, сосредоточенные силы и распределенные нагрузки, приложенные к балке (включая опорные реакции и компенсирующую распределенную нагрузку);
a, b – расстояние от начала координат до соответствующих моментов m и сил F;
c – расстояние от начала координат до сечения балки, где начинается действие распределенной нагрузки q.

Составляем уравнения МНП для заданной балки

Начало координат принимаем в крайнем правом сечении балки, так как оно расположено на опоре.

Распределенная нагрузка не доходит до конца балки, поэтому продляем её действие и на этой же длине добавляем компенсирующую нагрузку той же интенсивности но противоположного направления.

Запишем нагрузки в уравнения МНП последовательно по участкам с учетом знаков

Для определения начальных параметров θ₀ и y₀ запишем граничные условия.

На опорах прогибы балки равны нулю, т.е.
Из второго граничного условия, используя уравнение прогибов для точки B определим угол поворота сечения в начале координат θ₀
Откуда, при z=3м

Для построения линии изогнутой оси балки определим углы наклона сечений балки на опорах θ_B, θ_K и прогибы в характерных сечениях y_A, y_C, y_D.

Углы поворота сечений на опорах

Далее, для краткости, сократим дробь перед скобками
Линейные перемещения (прогибы) характерных сечений балки
Прогиб сечения A (y_z при z=3,6м)

Прогиб сечения C (y_z при z=1,8м)

Прогиб сечения D (y_z при z=0,6м)

Расчет максимальных прогибов балки

Экстремумы прогибов балки будут в точках, где угол наклона сечения балки равен нулю.

Для их определения, приравниваем к нулю уравнения углов наклона сечений по каждому участку балки, откуда определяем координаты z экстремумов прогибов на участке (если они есть).
1 участок (KD).
Уравнение решений не имеет (т.е. экстремумов на участке нет), это значит, что максимальный прогиб на этом участке будет на его левой границе (в сечении D), так как правая точка участка расположена на опоре.

2 участок (DC).

То есть, экстремум прогибов на втором участке будет на расстоянии z₂=0,782м от начала координат.

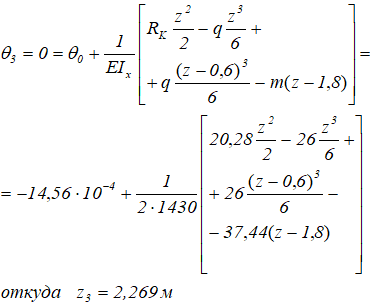
3 участок (CB).

Экстремум прогибов на третьем участке в сечении, на расстоянии z₃=2,269м от начала координат.

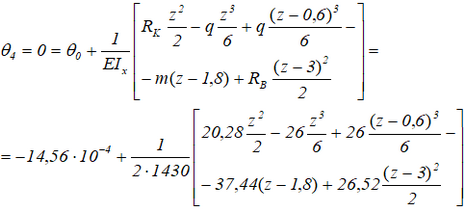
4 участок (BA).

Данное уравнение решений также не имеет, следовательно, максимальный прогиб на конце консоли, так как на правой границе участка – опора.

Значения максимальных прогибов балки на втором и третьем участках определяем из соответствующих уравнений прогибов для найденных значений z.

По полученным данным строим линию изогнутой оси балки в соответствии с эпюрой изгибающих моментов M_x и с указанием углов поворота сечений на опорах.

Проверка балки на жесткость

Проверяем балку на жесткость, сравнивая по модулю максимальные значения прогибов y_max в пролёте и на консольной части с допустимыми [f].

Балка считается жесткой, если прогибы её сечений не превышают допустимых значений, т.е.
Рассчитаем абсолютные значения допустимых прогибов заданной балки:
В пролете

На консольной части

Для проверки на жесткость сравниваем величину рассчитанных ранее максимальных прогибов сечений балки с соответствующими допустимыми значениями.

В пролете
На консоли
Как видно, максимальный прогиб на конце консольной части балки превышает соответствующее допустимое значение, следовательно, балка не удовлетворяет заданному условию жесткости.

Жесткость балки можно увеличить до требуемого значения путем увеличения момента инерции её сечения, т.е. подбором сечения большего размера.

Подберем двутавр другого номера, который будет обеспечивать необходимую жесткость балки.

Определяем, во сколько раз надо уменьшить величину максимального перемещения сечения.
Тогда, расчетный момент инерции нового сечения балки
По сортаменту выбираем двутавр №20 с осевым моментом инерции сечения I_x=1840см 4 .

Для начала требуется пересчитать угол наклона сечения балки в начале координат.

Рассчитываем прогиб сечения A с новым размером сечения

Условие жесткости выполняется.

Таким образом, двутавр №20 обеспечивает необходимую прочность и жёсткость заданной балки.
Полный расчет заданной балки на прочность и жёсткость выполнен.

Читайте также: