Проверить прочность стального бруса

Обновлено: 16.05.2024

Как и всякое сложное инженерное сооружение, конструкция летательных аппаратов для расчета на прочность мысленно расчленяется на отдельные узлы и отсеки, к которым прикладываются действующие на них в данный момент расчетные нагрузки и реактивные усилия, приходящие со стороны смежных мысленно отброшенных отсеков. В пределах каждого такого отсека или узла все действующие аэродинамические и инерционные нагрузки принимаются как статические. Таким образом, проверяются расчетным путем все элементы конструкции аппарата, переходя от одного момента нагружения к другому, т.е. по всем расчетным случаям. Самым ответственным моментом расчета является выбор и обоснование величины коэффициентов безопасности. Под коэффициентом безопасности f принято понимать число, больше единицы, на которое следует умножить величину эксплуатационной нагрузки (или перегрузки). Для самолетов значения коэффициентов безопасности устанавливаются «Авиационными правилами». После установления коэффициента безопасности все расчеты на прочность проводят на так называемые расчетные нагрузки (перегрузки), равные:

n р =f×n э , где

P р , n р - расчетные значения нагрузок (перегрузок),

P э , n э - эксплуатационные значения нагрузок (перегрузок),

f- коэффициент безопасности.

В результате расчета нужно получить ответ на вопрос, удовлетворяет или нет конструкция тем требованиям прочности, которые к ней предъявляются.

Наиболее распространенным методом расчета на прочность является расчет по допускаемым напряжениям. В основу этого метода положено предположение, что критерием прочности является напряженное состояние в точке. Последовательность расчета следующая. На основе анализа напряженного состояния конструкции выделяется точка, в которой возникает наибольшее напряжение. Найденная величина напряжения сравнивается с допускаемой величиной для материала конструкции. Из сопоставления расчетных напряжений и допускаемых напряжений делается заключение о прочности.

В ряде случаев достижение в точке максимальных напряжений предельных значений не является опасным для всей конструкции в целом. Такая ситуация возникает при неравномерном распределении напряжений по сечению, например при изгибе или кручении, а также для составных статически неопределимых конструкций. Если конструкция изготовлена из пластического материала, то достижение, в какой либо точке, предела текучести не приводит к потере её несущей способности. В связи с этим возникает необходимость к оценке прочности конструкции по её предельному состоянию. Под предельным состоянием конструкции понимают такое её состояние, при котором она теряет способность сопротивляться внешним воздействиям, или перестает удовлетворять предъявляемым к ней эксплуатационным требованиям. Различают три вида предельных состояний.

1. Предельное состояние по несущей способности. При достижении этого состояния, например, в результате исчерпания статической прочности, потере устойчивости или достижении длины усталостной трещины предельной величины, конструкция теряет возможность сопротивляться внешним воздействиям.

2. Предельное состояние по развитию чрезмерных деформаций. В этом случае от действия статических или динамических нагрузок или от действия температуры при сохранении статической прочности и устойчивости появляются такие остаточные изменения или колебания, при которых конструкция перестает удовлетворять предъявляемым к ней требованиям.

3. Предельное состояние по образованию и развитию трещин. Такое состояние возникает, когда в конструкции, сохраняющей статическую прочность, появляются трещины таких размеров, что дальнейшая эксплуатация становится невозможной, например, вследствие потери герметичности.

На практике наиболее часто встречаются два случая расчета статической прочности по допускаемым напряжениям.

Проектировочный расчет. В этом случае по известным нагрузкам и для выбранного материала требуется определить необходимые размеры поперечного сечения элемента конструкции, обеспечивающие его надежную работу. В основе этого расчета для одноосного напряженного состояния лежит условие прочности:

выражающее тот факт, что наибольшее напряжение (нормальное s_max или касательное τ_max) действующее в сечении элемента конструкции не должно превышать соответствующего допускаемого напряжения [s_max] ([τ_max]). Допускаемое напряжение определяют как частное от деления предельных напряжений s_пред (τ_пред) на запас прочности n_s (n_τ):

В качестве предельных напряжений принимают предел прочности s_в (τ_в). для хрупких материалов и предел текучести s_т (τ_т) для пластических материалов.

При установлении запаса прочности n_s (n_τ) учитывают разброс механических свойств материала, отступления в геометрии элементов конструкции, хотя бы в пределах допусков.

2. Проверочный расчет. Проводят в случае, когда заданы размеры элемента конструкции и его материал. Требуется выяснить, может ли заданный элемент выдержать, не разрушаясь, заданную нагрузку. В этом случае определяют избытки прочности h_s (h_τ) как отношение допускаемых напряжений к максимальным действующим напряжениям:

Аналогично проводят расчет на жесткость, только вместо условия прочности записывают условие жесткости, ограничивающее величину деформаций (или перемещений). Однако даже в том случае, когда выполнен расчет на жесткость, всегда необходимо проводить проверочный расчет на прочность и, если он дает отрицательный результат, то следует принять размеры, полученные из расчета на прочность.

Считается, что стержневая система или ступенчатый брус разрушаться, если максимальное нормальное напряжение, возникающее в них, достигнет предельного напряжения материала, из которого они выполнены.

Условие разрушения имеет вид:

Наибольшее действующее напряжение определяют для наиболее напряженного стержня системы или сечения бруса по формуле:

N- нормальное усилие,

F- площадь поперечного сечения.

В качестве предельных напряжений s_пред примем те напряжения, при достижении которых в материале появляются признаки нарушения прочности: при достижении предела текучести s_т‑ заметные остаточные деформации, при достижении предела прочности s_в - появление излома. Таким образом, для пластичных материалов предельным напряжением будет предел текучести: s_тр ‑ предел текучести при растяжении, или s_тс ‑ предел текучести при сжатии. Для хрупких материалов предельным напряжением будет предел прочности: s_вр ‑ предел прочности при растяжении, или s_вс ‑ предел прочности при сжатии.

Следовательно, можно записать:

Стержневая система или ступенчатый брус считаются прочными, если максимальные расчетные напряжения, возникающие в них, будут меньше допускаемых напряжений. Это означает, что для стержневой системы или ступенчатого бруса, обладающих достаточной прочностью, должно выполняться условие прочности:

s_max - наибольшее действующее напряжение,

[s]-допускаемое напряжение.

Допускаемое напряжение [s] определим как то максимальное напряжение, которое можно допустить при работе и при котором будет обеспечен требуемый запас прочности:

s_пред- предельное напряжение,

n_s - запас прочности.

Если возникает необходимость соблюдения требования необходимой жесткости, т.е. способности воспринимать заданные внешние нагрузки, не деформируясь выше установленных норм, то необходимо удовлетворить условию жесткости, которое требует, чтобы максимальное перемещение узла d_max стержневой системы или сечения ступенчатого бруса не превышало допускаемого перемещения [d]:

Если получены два значения искомого размера (один из условия прочности, другой из условия жесткости), тогда в качестве окончательного принимают тот, который удовлетворяет обоим условиям, т.е. наибольший.

Подобрать сечение стержней фермы крепления двигателя (рис. 10.1) для случая нагружения двигателя силой тяги P э _x и массовыми силами соответствующими случаю D. Вес двигателя G_дв = 10 кН; тяга P э _x =30 кН; перегрузка n_D=-2,5; коэффициент безопасности f=1,5. Стержни фермы выполнены из тонкостенных стальных труб с отношением внутреннего диаметра к наружному d/D=0,9. Материал труб 30ХГСА. Предел текучести на растяжение s_0,2=1162 МПа, предел текучести на сжатие s_{0,2 сж}=1081 МПа.

1. Определим расчетные нагрузки путем учета коэффициента безопасности и перегрузки в заданном случае нагружения.

2. Двигатель крепится с помощью шести стержней. Так как для пространственной системы сил можно составить шесть уравнений равновесия, то система является статически определимой. Для определения усилий в стержнях удалим опоры, и их действие заменим неизвестными усилиями в стержнях (рис. 10.2).

В силу симметрии можно записать:

Для определения усилий в стержнях составим уравнения равновесия:

Решая систему уравнений, получим усилия в стержнях:

Из рассмотрения схемы нагружения определим:

Вычислим численные значения усилий в стержнях:

3. Определим напряжения в стержнях:

4. Диметры стержней определим из условий:

Для ступенчатого стального бруса (рис. 10.3а) определить реакции в заделках, построить эпюры продольных сил N, нормальных напряжений s, относительных деформаций e, продольных перемещений Dl. Определить опасное сечение и подобрать необходимую площадь F из условия прочности на растяжение или сжатие.

Задано: a =0,5 м, q=200 кН/м, E = 2,1´10 5 МПа. Допускаемое напряжение на растяжение [s]_р = 160 МПа, на сжатие [s]_c = 60 МПа.

1.Отбросим левую и правую заделку и заменим их действие неизвестными силами Х₁ и Х₄. Нумеруем характерные сечения (рис. 10.3б).

2. Запишем уравнение равновесия:

Задача один раз статически неопределима, так число уравнений равновесия на единицу меньше числа неизвестных.

3.Запишем выражение нормальных сил N на каждом участке, последовательно отсекая сечения от начала участка, начиная от левой заделки.

4. Учитывая, что смещение заделок относительно друг друга равно нулю, запишем уравнение совместимости деформаций:

По закону Гука удлинение каждого участка стержня имеет вид:

Следовательно, уравнение совместимости примет вид:

Решая уравнения 1 и 2 совместно, получим:

5.Запишем выражения нормальных сил, подставив значение Х₁:

Строим эпюру N (рис. 10.3в).

6. Запишем выражения нормальных напряжений:

Строим эпюру s (рис. 10.3г).

7.Запишем выражения относительных деформаций:

Строим эпюру e (рис. 10.3д).

8. Запишем выражения перемещений сечений:

Строим эпюру Dl (рис. 10.3е).

Вычислим значение экстремума на эпюре Dl:

9. Запишем условия прочности:

Определяем потребную площадь сечения:

F>=9/14(qa/[s]_р)=9/14(200 10 3 0,5/160 10 6 )=4 10 -4 м 2

F>=-5/7(qa/[s]_с)=-5/7(200 10 3 0,5/(-60 10 6 ))=11,9 10 -4 м 2

Ознакомиться с примером построения эпюр продольных сил, напряжений и перемещений.

Задача 1.Двухступенчатый стальной брус нагружен силами F₁=30 кН F₂=40 кН.

Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А₁=1,5см 2 ;А ₂=2см 2 .

Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.

Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Разбиваем брус на участки.

Определяем ординаты эпюры N на участках бруса:

Строим эпюру продольных сил

Вычисляем ординаты эпюры нормальных напряжений

σ₁ = = –200МПа

σ₂ = = –150МПа

σ ₃= =50МПа

Строим эпюры нормальных напряжений.

4. Проверяем прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Выбираем максимальное по модулю расчетное напряжение. Iσ_maxI = 200 МПа

Подставляем в условие прочности Iσ_maxI ≤ [σ]

200 МПа ≤ 160 МПа. Делаем вывод, что прочность не обеспечена.

5. Определяем перемещение свободного конца бруса Е = 2∙10 5 МПа.

∆l=∆l₁+∆l₂+∆l₃

∆l₁= = – 0,5мм

∆l₂= = – 0,225мм

∆l₃= = 0,05мм

∆l= - 0,5 – 0,225 + 0,05 = – 0,675мм

Брус укоротился на 0,675мм

1. Задание: Решить задачи

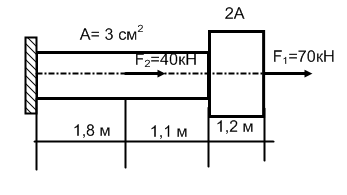
Двухступенчатый стальной брус нагружен силами F₁, F₂.

Разбить брус на участки. Пронумеровать эти участки.

Найти величину продольной силы на первом участке.

Найти величину продольной силы на втором участке.

Найти величину продольной силы на третьем участке.

Построить эпюру для продольной силы.

Найти величину нормального напряжения на первом участке.

Найти величину нормального напряжения на втором участке.

Найти величину нормального напряжения на третьем участке.

Построить эпюру для нормального напряжения.

Проверить прочность бруса. Допускаемое напряжение [σ] = 160 МПа.

Определить перемещение свободного конца бруса.

Задание 2

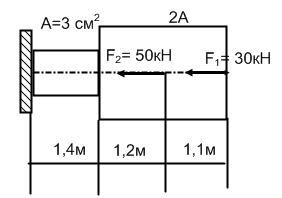
Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Задание 3

Литература
В.П. Олофинская «Техническая механика» курс лекций с вариантами практических и тестовых заданий.
Лекции по теме (конспекты).

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Статически определимые задачи. Р-С

Задача

Для статически определимого стального ступенчатого бруса построить эпюры продольных сил, нормальных напряжений и перемещений. Проверить прочность бруса. Материал – сталь Ст 3, модуль продольной упругости Е=2·10 5 МПа, допускаемое напряжение [σ]=160МПа.

Определяем продольные силы N методом сечений. Сечение расставляем на характерных участках (между изменениями). Подсказкой может служить размерная нитка – сколько отсечено отрезков, столько будет и участков с сечениями. В нашей задаче их 6.Каждое сечение рассматриваем отдельно с любой стороны на наше усмотрение. Силу N направляем от сечения.

Строим эпюру N. Все значения откладываем перпендикулярно от нулевой линии в выбранном нами масштабе.

Положительные значения условимся откладывать вправо от нулевой линии, отрицательные — влево.

Строим эпюру σ.

Проверим прочность по условию прочности

Прочность обеспечена.

4. Определяем перемещение бруса.

Расчет ведется от стены, в которой перемещение равно нулю ω_А= 0.

Формула Гука для определения абсолютной деформации участка

Определяем перемещения:

Строим эпюру перемещений ω.

Для ступенчатого стального стержня требуется построить эпюры нормальных сил и напряжений, проверить прочность стержня по допускаемым напряжениям согласно условию прочности, построить эпюру линейных перемещений. Дано:Схема стержня; эпюры нормальных сил, напряжений и перемещений

Расчет нормальных (продольных) сил проводится с помощью метода сечений путем рассмотрения характерных сечений для силовых участков.

Участок ВС:

Участок СD:

Участок DK:

Эпюра нормальных сил — рис. б.

Расчет нормальных напряжений на участках:

Эпюра нормальных напряжений — рис. в.

Расчет перемещений характерных сечений.

Перемещения сечений вниз считаются положительными, а вверх – отрицательными. Расчет ведем от стены, в которой перемещение равно 0

Эпюра перемещений — рис. г.

Проверим прочность стержня. Согласно эпюре нормальных напряжений: Следовательно, условие прочности не выполняется. Перенапряжение в опасных сечениях составляет:

Задача на стальной ступенчатый брус

Ступенчатый стержень закреплен одним концом и нагружен сосредоточенными силами. Длины участков бруса равны ℓ₁, ℓ₂, ℓ₃ площади их поперечных сечений А₁, А₂, А₃. Материал бруса – сталь. Построить эпюры внутренних сил N, напряжений σ и основных перемещений ∆ℓ.

1) Определим продольные силы:

2) Определим напряжения на всех участках:

3) Строим эпюру перемещений: (нарастающим итогом, начиная от опоры, в которой перемещение равно нулю)

Задача 6

Определить усилия в стержнях, поддерживающих жесткую емкость.

Не останавливаясь на определении опорных реакций R₁, R₂ и R₃, сразу используем метод сечений и рассматриваем равновесие верхней части сооружения:

Задача 5

Стальной ступенчатый брус нагружен силами. Для статически определимого стального ступенчатого бруса построить эпюры: продольных сил, нормальных напряжений и перемещений.

1) Прежде всего брус «разбивается» на участки, границами которых являются:– точки приложения внешних сил (отмечены крестиком),– места резкого изменения размеров поперечных сечений,– места, где меняется вид материала.

1) Определяем опорную реакцию. С этой целью на схеме бруса следует обязательно задаться направлением реакции и принять для нее буквенное обозначение. Например, А (см.схему)

Чрезвычайно важно правильно отреагировать на отрицательный знак реакции. Он означает, что истинное направление реакции противоположно предполагаемому. Поэтому следует зачеркнуть (!) и вектор, и буквенное обозначение (двумя наклонными линиями), а затем показать противоположный вектор и рядом указать абсолютную величину реакции без всякого буквенного обозначения и в дальнейших выкладках «бывшая» отрицательная реакция нигде не должна появляться!

2) С целью построения эпюры продольных сил (N) необходимо определять ее не в конкретных сечениях, а в произвольных сечениях каждого участка (чтобы иметь функциональную зависимость). Для этого приходится применять метод сечений для произвольного сечения каждого участка:

— на I участке:

— на II участке:

— на III участке:

N.B.: неизвестное усилие всегда (!) следует предполагать положительным и направлять в соответствии с принятым правилом знаков. В частности положительная продольная сила растягивающая и потому должна направляться «от сечения».

3) Напряжения при растяжении-сжатии вычисляются по формуле:

причем знак напряжения повторяет знак продольной силы N.

4) При построении эпюры перемещений следует вспомнить, что любая ее ордината означает смещение сечения, расположенного под этой ординатой, по отношению к неподвижному сечению.

А поэтому построение и начинается с неподвижного сечения. В нашем случае неподвижным является нижнее сечение, расположенное в опоре. Обозначим его номером (0): δ₍₀₎=0.

Перемещение сечения (1) на границе между III и II участками бруса будет равно абсолютной деформации III го участка:

Перемещение сечения (2) на границе II и I го участков складывается из смещения сечения (1) и абсолютной деформации участка II:

Перемещение верхнего сечения (3) сложится из смещения сечения (2) и абсолютной деформации I го участка:

Заметим: все эпюры штрихуются только перпендикулярно к оси, поскольку наклонные штрихи не имеют физического смысла!

Задача 4

Определить усилия в стержнях

Не задерживаясь на определении опорных реакций, сразу будем искать усилия в стержнях с помощью метода сечений. Пунктиром показан замкнутый разрез, посредством которого система распадается на три части: верхнюю, среднюю и нижнюю. Для решения задачи достаточно рассмотреть равновесие средней части и нижней части системы. Неизвестные усилия в перерезанных стержнях предполагаем положительными, то есть растягивающими:

Уравнения равновесия нижней части:

Из (3) находим

Уравнения равновесия средней части:

Из (3´):

Задача 3

Абсолютно жесткий брус прикреплен двумя стержнями к потолку и одним к полу. Определить усилия в стержнях.

В опорных точках возможно возникновение трех опорных реакций. Для их определения имеются три уравнения равновесия. Следовательно, задача статически определима.

Поскольку нас интересуют внутренние усилия в стержнях, то реакции можно и не определять, а сразу использовать метод сечений. Вырезаем замкнутым сечением среднюю часть системы и рассматриваем ее равновесие (неизвестные усилия предполагаем положительными, т.е. растягивающими):

Из (3):

α=45˚, и тогда:

Задача 2

Определить допускаемую нагрузку на кронштейн и опускание точки В, если [σ]=160МПа, Е=2·10 11 Па.

Сначала необходимо найти усилие в стержне CD, сохраняя нагрузку в общем (буквенном) виде. С этой целью используем метод сечений: мысленно перережем стержень CD в любом его сечении и рассмотрим равновесие нижней части:

Составим уравнения равновесия:

Уравнение (3) позволяет найти усилие в стержне:

Условие прочности:

Площадь круглого сечения

После подстановок в условие прочности имеем:

Допускаемая величина нагрузки соответствует случаю полного равенства в условии прочности, откуда:

Величину опускания точки В при действии найденной нагрузки найдем, рассмотрев картину деформации системы:

Из подобия треугольников АСС₁ и АВВ₁ вертикальное смещение точки В будет:

Условие прочности при растяжении-сжатии

Условие прочности при растяжении и сжатии: нормальные напряжения σ в сечениях бруса не должны превышать заданных допустимых напряжений [σ].

При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ . Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:

Здесь
σ _max – максимальные расчетные нормальные напряжения в стержне,
N – внутренние продольные силы (принимаются с построенных эпюр),
А – соответствующая площадь поперечного сечения бруса,
[ σ ] – допустимые напряжения (расчетное сопротивление) для материала стержня, определяемое как:

n – коэффициент запаса прочности, устанавливаемый нормативными документами.

Данное условие означает что для того чтобы стержень при растяжении-сжатии оставался прочным, напряжения σ в его сечениях не должны превышать допустимых значений [ σ ].

В случаях, когда для материала стержней допустимые напряжения на растяжение [ σ ]_р и на сжатие [ σ ]_сж отличаются, при сравнении необходимо учитывать знак напряжений σ , который зависит только от знака соответствующих внутренних сил N.

Так, положительные значения напряжений σ сравниваются с [ σ ]_р, отрицательные напряжения по модулю не должны превышать значения [ σ ]_сж.

Три задачи расчета на прочность

Данное условие прочности позволяет решать три основных задачи сопротивления материалов и технической механики:

Проверка на прочность.

В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ , после чего максимальная из них сравнивается с заданным допустимым значением [ σ ].

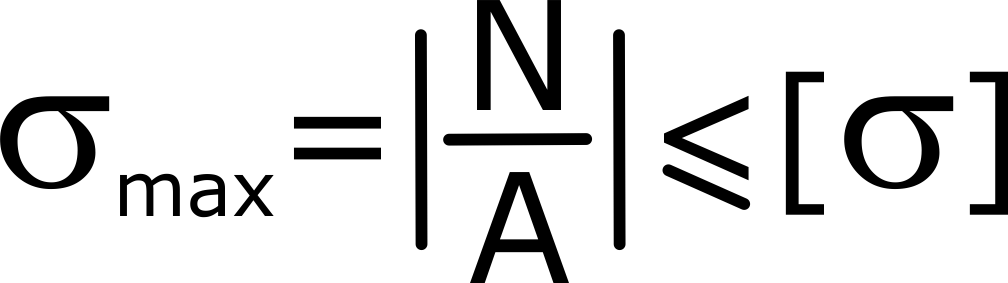
Ответ в данной задаче дается в виде заключения:

если σ _max ≤ [ σ ] стержень прочный,
если σ _max > [ σ ] стержень непрочный.

Подбор размеров сечения (проектировочный расчет)

Эта задача является основной в технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.

Для этого условие прочности записывается относительно искомой величины.

Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.

Определение грузоподъемности стержня.

Данная формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней силы, которую может выдержать стержень, оставаясь прочным.

В данном случае условие прочности записано относительно внутренней силы N.

Полный расчет балки на прочность и жесткость

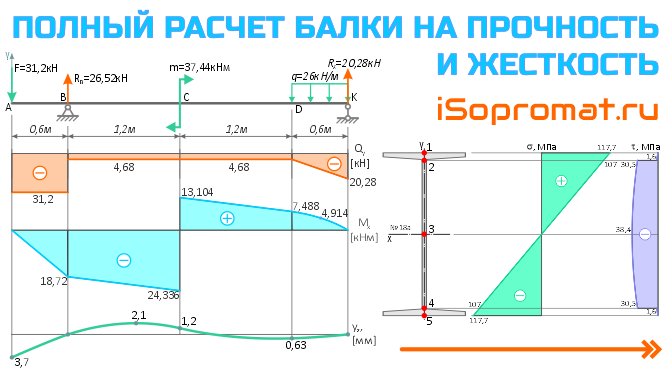
Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки при заданной системе внешних изгибающих нагрузок.

Задача

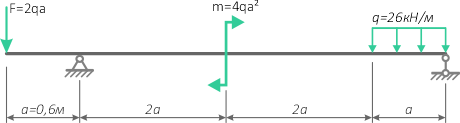
Выполнить полный расчёт на прочность и проверить жёсткость стальной, двутавровой, статически определимой балки на двух опорах

при следующих данных:
Интенсивность равномерно распределенной нагрузки q=26кН/м, продольный размер a=0,6м, сосредоточенная сила F=2qa, изгибающий момент m=4qa 2 .
Допускаемые нормальные напряжения [σ]=160МПа,
Модуль упругости I рода Е=200ГПа.
Допустимый прогиб балки [f]=l/400.

Последовательность решения задачи
Для расчета балки на прочность

Вычерчивается схема нагружения в масштабе, с указанием числовых значений приложенных нагрузок;
Строятся эпюры внутренних силовых факторов Q_y и M_x;
По условию прочности подбирается двутавровое сечение (№ двутавра) стальной балки:
Для балки двутаврового профиля выполняется полная проверка на прочность, приняв
Проверяется прочность по главным напряжениям в опасных точках сечения по III гипотезе прочности
По результатам расчетов дается заключение о прочности балки при выбранном сечении.
В случае невыполнения условия прочности по главным напряжениям, подбирается новый номер двутавра.

Для расчета балки на жесткость

С использованием универсальных уравнений метода начальных параметров (МНП) определяются углы поворота θ над опорами и прогибы в характерных сечениях (2-3 сечения), а также, максимальные прогибы балки в пролете и консольной части;
По этим данным, в соответствии с эпюрой M_x, строится линия изогнутой оси балки;
Проверяется выполнение условия жесткости балки.
Если условие жесткости не удовлетворяется, подбирается новое двутавровое сечение, обеспечивающее необходимую жесткость.

Решение

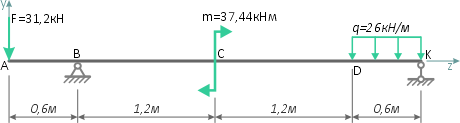
Рассчитаем численные значения силы F и момента m, которые были заданы в виде переменных.
Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.

Показываем оси системы координат y-z и обозначаем характерные сечения балки.

Полный расчет стальной балки на прочность

Определение реакций в шарнирных опорах балки

Направим реакции опор вверх и запишем суммы моментов относительно точек на опорах, нагрузок приложенных к балке

Из составленных уравнений выражаем и находим реакции.
Из первого уравнения
из второго
Положительные значения указывают на то, что произвольно заданное направление реакций вверх оказалось верным.

Выполним проверку найденных реакций опор спроецировав все силы на ось y
Равенство суммы проекций сил нулю говорит о том что реакции опор определены правильно.

Более подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

Построение эпюр внутренних силовых факторов

Рассчитаем значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.

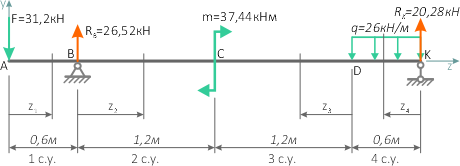
Балка имеет 4 силовых участка.

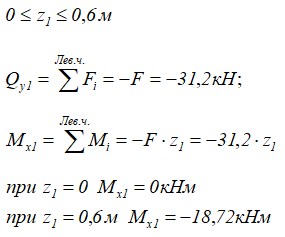
1 участок (AB)

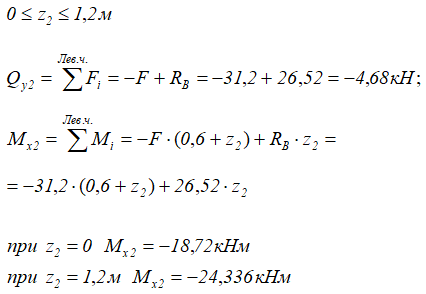
2 участок (BC)

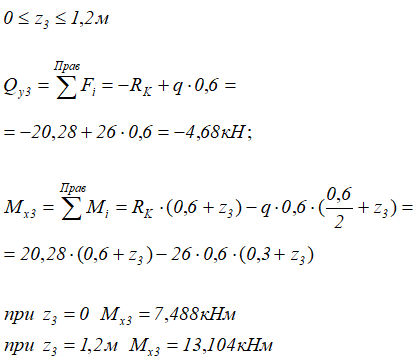
3 участок (CD)

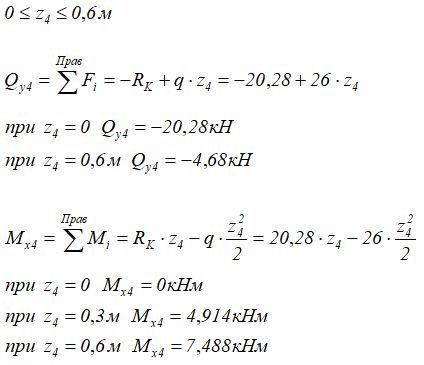
4 участок (DK)

Здесь, значения Q_y на границах участка имеют одинаковый знак, поэтому на этом участке, на эпюре M_x экстремума не будет.

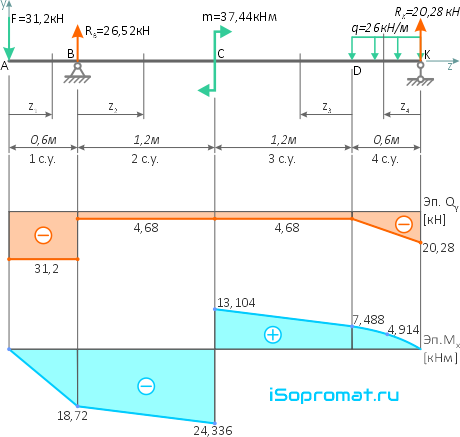
По полученным данным строим эпюры внутренних поперечных сил Q_y и изгибающих моментов M_x.

Проверка построенных эпюр:
— по дифференциальным зависимостям
— в сечениях балки, где приложены сосредоточенные силы, на эпюре Q_y имеются скачки значений на величину соответствующей силы;
— в сечениях балки, где приложены изгибающие моменты, на эпюре M_x скачки значений на величину соответствующего момента.
Все условия выполнены, следовательно, эпюры построены верно.

По эпюрам видно, что опасным является сечение балки в точке C, где:
M_x=M_{x max}=-24,336кНм
Q_y=-4,68кН

Подбор двутаврового сечения балки

Подберем двутаврового сечение балки по условию прочности по нормальным напряжениям
где
M_{x max} – максимальное значение внутреннего изгибающего момента в сечениях балки. Принимается с построенной эпюры M_x;
W_x – осевой момент сопротивления поперечного сечения балки относительно горизонтальной оси x;
[σ] – допустимые нормальные напряжения.

Выразим и рассчитаем минимально необходимое значение осевого момента сопротивления поперечного сечения балки W_x обеспечивающего её прочность по нормальным напряжениям
По сортаменту прокатной стали выбираем номер двутавра имеющий осевой момент сопротивления близкий к расчетному W_x=152,1см 3 в большую сторону.

Это двутавр №18а у которого W_x=159,0см 3 .

Максимальные нормальные напряжения в сечении

Этот двутавр будет работать при максимальных нормальных напряжениях в крайних слоях опасного сечения балки.

Максимальные нормальные напряжения выбранного номера двутавра не превышают допустимых значений, значит сечение подобрано верно.

Полная проверка на прочность двутаврового сечения

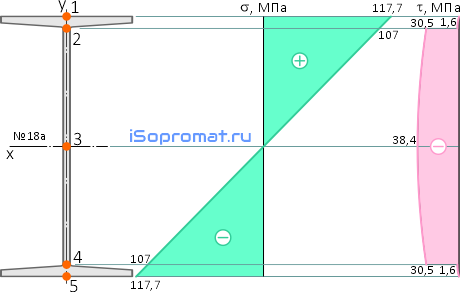
При изгибе тонкостенных прокатных профилей, таких как, например, двутавр или швеллер, в местах соединения стенки с полкой нормальные и касательные напряжения имеют не максимальные, но достаточно большие значения.

Их совместное действие, выраженное в виде главных (эквивалентных) напряжений, может превышать допустимые значения, что будет означать потерю прочности в этих точках поперечного сечения балки.

В отношении главных напряжений неблагоприятным является сечение балки B, в котором максимально значение поперечной силы при значительном изгибающем моменте:

Для полной проверки на прочность построим эпюры нормальных и касательных напряжений в сечении B для выбранного номера двутавра.

Построение эпюр нормальных и касательных напряжений в сечении балки подробно рассмотрено здесь:

Для выполнения расчетов, из сортамента выпишем необходимые геометрические характеристики выбранного номера двутавра:
Высота сечения
h=180мм;
Ширина сечения
b=100мм;
Толщина стенки
d=5,1мм;
Толщина полки
t=8,3мм;
Осевой момент инерции поперечного сечения
I_x=1430см 4 ;
Статический момент сечения
S_x=89,8см 3 .

Двутавровое сечение по высоте имеет 5 характерных точек: верхнюю (1), нижнюю (5), среднюю (3) и две точки в местах перехода стенки в полку двутавра (2 и 4).

Для построения эпюр, определим значения напряжений в указанных точках сечения.

Нормальные напряжения в сечении балки распределяются по линейному закону, поэтому для построения эпюры достаточно найти максимальные значения
Касательные напряжения в характерных точках сечения рассчитываются по формуле Журавского
где
Q_y — поперечная сила в данном сечении. Принимается с эпюры с учетом знака;
I_x – осевой момент инерции поперечного сечения;
b_y – ширина сечения на уровне рассматриваемой точки;
S_x* — статический момент части сечения, расположенной между уровнем рассматриваемой точки и верхним (нижним) краем сечения.

Рассчитаем значения касательных напряжений

Так как выше точки 1 и ниже точки 5 площадь сечения равна нулю, то статический момент S_x* для этих точек тоже равен нулю, следовательно
В точке 3

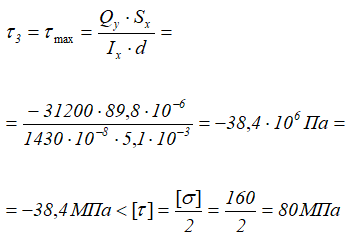
В точке 3 будут максимальные касательные напряжения, т.к. для неё статический момент сечения S_x максимальный при минимальной ширине сечения d

Видно, что прочность сечения по касательным напряжениям обеспечена.

В точках, где стенка двутавра переходит в полку, будут скачки напряжений, так как на уровне этих точек резко меняется ширина сечения

Рассчитаем значения напряжений в этих точках для стенки (с) и полки (п)

Статический момент полки двутавра
Касательные напряжения в точках 2 и 4 полки
Касательные напряжения в точках 2 и 4 стенки
По этим данным строим эпюры нормальных и касательных напряжений для выбранного номера двутавра.

Рассчитаем величину главных напряжений в точках соединения полки со стенкой двутавра (т. 2 и 4)

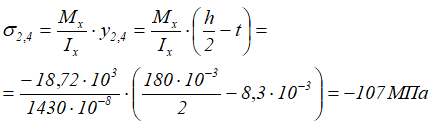
Нормальные напряжения в рассматриваемых точках

Эквивалентные напряжения в опасных точках сечения
Как видно, величина эквивалентных напряжений не превышает допустимых значений, следовательно, выбранный номер двутавра удовлетворяет условию прочности и по главным напряжениям.

Полный расчет балки на жесткость

Для того чтобы балка удовлетворяла условию жесткости, линейные перемещения (прогибы) балки y_z не должны превышать заданных допустимых значений [f], т.е. должно выполняться условие жесткости

Расчет перемещений сечений балки

Расчет перемещений сечений балки выполним методом начальных параметров (МНП).

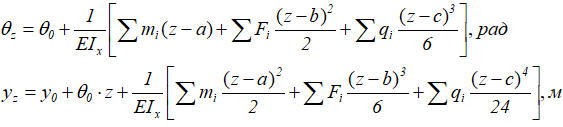
Шаблоны уравнений метода начальных параметров имеют вид:

Здесь:
θ_z — угловое перемещение (угол наклона) рассматриваемого сечения;
y_z — вертикальное линейное перемещение (прогиб) рассматриваемого сечения балки;
z – расстояние от выбранного начала координат балки до рассматриваемого сечения (координата);
θ₀, y₀ — соответственно угловое и линейное перемещения балки в выбранном начале координат (начальные параметры);
E – модуль упругости I рода для материала балки;
I_x – осевой момент инерции сечения балки;
m, F, q – соответственно моменты, сосредоточенные силы и распределенные нагрузки, приложенные к балке (включая опорные реакции и компенсирующую распределенную нагрузку);
a, b – расстояние от начала координат до соответствующих моментов m и сил F;
c – расстояние от начала координат до сечения балки, где начинается действие распределенной нагрузки q.

Составляем уравнения МНП для заданной балки

Начало координат принимаем в крайнем правом сечении балки, так как оно расположено на опоре.

Распределенная нагрузка не доходит до конца балки, поэтому продляем её действие и на этой же длине добавляем компенсирующую нагрузку той же интенсивности но противоположного направления.

Запишем нагрузки в уравнения МНП последовательно по участкам с учетом знаков

Для определения начальных параметров θ₀ и y₀ запишем граничные условия.

На опорах прогибы балки равны нулю, т.е.
Из второго граничного условия, используя уравнение прогибов для точки B определим угол поворота сечения в начале координат θ₀
Откуда, при z=3м

Для построения линии изогнутой оси балки определим углы наклона сечений балки на опорах θ_B, θ_K и прогибы в характерных сечениях y_A, y_C, y_D.

Углы поворота сечений на опорах

Далее, для краткости, сократим дробь перед скобками
Линейные перемещения (прогибы) характерных сечений балки
Прогиб сечения A (y_z при z=3,6м)

Прогиб сечения C (y_z при z=1,8м)

Прогиб сечения D (y_z при z=0,6м)

Расчет максимальных прогибов балки

Экстремумы прогибов балки будут в точках, где угол наклона сечения балки равен нулю.

Для их определения, приравниваем к нулю уравнения углов наклона сечений по каждому участку балки, откуда определяем координаты z экстремумов прогибов на участке (если они есть).
1 участок (KD).
Уравнение решений не имеет (т.е. экстремумов на участке нет), это значит, что максимальный прогиб на этом участке будет на его левой границе (в сечении D), так как правая точка участка расположена на опоре.

2 участок (DC).

То есть, экстремум прогибов на втором участке будет на расстоянии z₂=0,782м от начала координат.

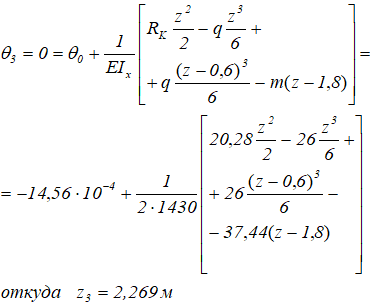
3 участок (CB).

Экстремум прогибов на третьем участке в сечении, на расстоянии z₃=2,269м от начала координат.

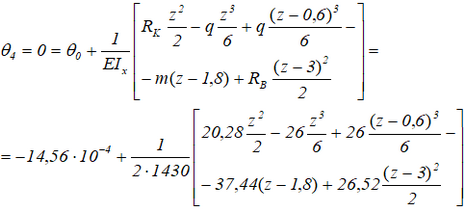
4 участок (BA).

Данное уравнение решений также не имеет, следовательно, максимальный прогиб на конце консоли, так как на правой границе участка – опора.

Значения максимальных прогибов балки на втором и третьем участках определяем из соответствующих уравнений прогибов для найденных значений z.

По полученным данным строим линию изогнутой оси балки в соответствии с эпюрой изгибающих моментов M_x и с указанием углов поворота сечений на опорах.

Проверка балки на жесткость

Проверяем балку на жесткость, сравнивая по модулю максимальные значения прогибов y_max в пролёте и на консольной части с допустимыми [f].

Балка считается жесткой, если прогибы её сечений не превышают допустимых значений, т.е.
Рассчитаем абсолютные значения допустимых прогибов заданной балки:
В пролете

На консольной части

Для проверки на жесткость сравниваем величину рассчитанных ранее максимальных прогибов сечений балки с соответствующими допустимыми значениями.

В пролете
На консоли
Как видно, максимальный прогиб на конце консольной части балки превышает соответствующее допустимое значение, следовательно, балка не удовлетворяет заданному условию жесткости.

Жесткость балки можно увеличить до требуемого значения путем увеличения момента инерции её сечения, т.е. подбором сечения большего размера.

Подберем двутавр другого номера, который будет обеспечивать необходимую жесткость балки.

Определяем, во сколько раз надо уменьшить величину максимального перемещения сечения.
Тогда, расчетный момент инерции нового сечения балки
По сортаменту выбираем двутавр №20 с осевым моментом инерции сечения I_x=1840см 4 .

Для начала требуется пересчитать угол наклона сечения балки в начале координат.

Рассчитываем прогиб сечения A с новым размером сечения

Условие жесткости выполняется.

Таким образом, двутавр №20 обеспечивает необходимую прочность и жёсткость заданной балки.
Полный расчет заданной балки на прочность и жёсткость выполнен.

Читайте также: